SPDE priors for uncertainty quantification of end-to-end neural data assimilation schemes

The spatio-temporal interpolation of large geophysical datasets has historically been adressed by Optimal Interpolation (OI) and more sophisticated model-based or data-driven DA techniques. In the last ten years, the link established between Stochastic Partial Differential Equations (SPDE) and Gaussian Markov Random Fields (GMRF) opened a new way of handling both large datasets and physically-induced covariance matrix in Optimal Interpolation. Recent advances in the deep learning community also enables to adress this problem as neural architecture embedding data assimilation variational framework. The reconstruction task is seen as a joint learning problem of the prior involved in the variational inner cost and the gradient-based minimization of the latter: both prior models and solvers are stated as neural networks with automatic differentiation which can be trained by minimizing a loss function, typically stated as the mean squared error between some ground truth and the reconstruction. In this work, we draw from the SPDE-based Gaussian Processes to estimate complex prior models able to handle non-stationary covariances in both space and time and provide a stochastic framework for interpretability and uncertainty quantification. Our neural variational scheme is modified to embed an augmented state formulation with both state and SPDE parametrization to estimate. Instead of a neural prior, we use a stochastic PDE as surrogate model along the data assimilation window. The training involves a loss function for both reconstruction task and SPDE prior model, where the likelihood of the SPDE parameters given the true states is involved in the training. Because the prior is stochastic, we can easily draw samples in the prior distribution before conditioning to provide a flexible way to estimate the posterior distribution based on thousands of members.

Neural SPDE solver for uncertainty quantification in high-dimensional space-time dynamics

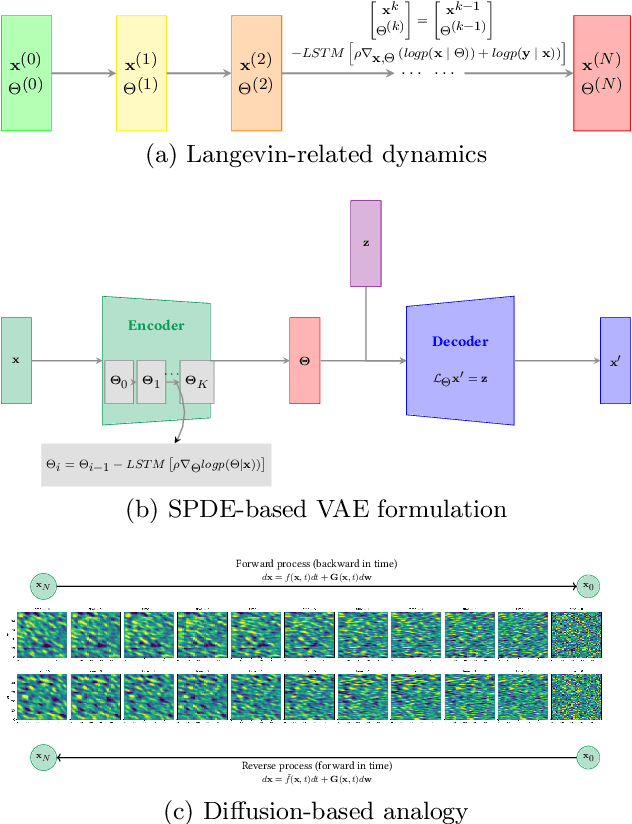
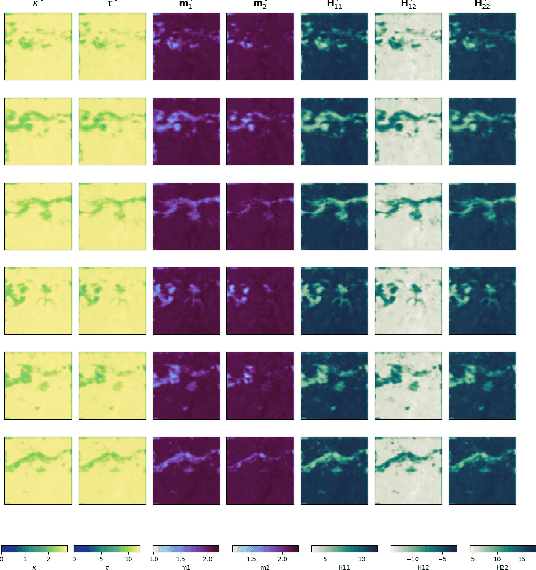
Historically, the interpolation of large geophysical datasets has been tackled using methods like Optimal Interpolation (OI) or model-based data assimilation schemes. However, the recent connection between Stochastic Partial Differential Equations (SPDE) and Gaussian Markov Random Fields (GMRF) introduced a novel approach to handle large datasets making use of sparse precision matrices in OI. Recent advancements in deep learning also addressed this issue by incorporating data assimilation into neural architectures: it treats the reconstruction task as a joint learning problem involving both prior model and solver as neural networks. Though, it requires further developments to quantify the associated uncertainties. In our work, we leverage SPDEbased Gaussian Processes to estimate complex prior models capable of handling nonstationary covariances in space and time. We develop a specific architecture able to learn both state and SPDE parameters as a neural SPDE solver, while providing the precisionbased analytical form of the SPDE sampling. The latter is used as a surrogate model along the data assimilation window. Because the prior is stochastic, we can easily draw samples from it and condition the members by our neural solver, allowing flexible estimation of the posterior distribution based on large ensemble. We demonstrate this framework on realistic Sea Surface Height datasets. Our solution improves the OI baseline, aligns with neural prior while enabling uncertainty quantification and online parameter estimation.

Learning Neural Optimal Interpolation Models and Solvers

The reconstruction of gap-free signals from observation data is a critical challenge for numerous application domains, such as geoscience and space-based earth observation, when the available sensors or the data collection processes lead to irregularly-sampled and noisy observations. Optimal interpolation (OI), also referred to as kriging, provides a theoretical framework to solve interpolation problems for Gaussian processes (GP). The associated computational complexity being rapidly intractable for n-dimensional tensors and increasing numbers of observations, a rich literature has emerged to address this issue using ensemble methods, sparse schemes or iterative approaches. Here, we introduce a neural OI scheme. It exploits a variational formulation with convolutional auto-encoders and a trainable iterative gradient-based solver. Theoretically equivalent to the OI formulation, the trainable solver asymptotically converges to the OI solution when dealing with both stationary and non-stationary linear spatio-temporal GPs. Through a bi-level optimization formulation, we relate the learning step and the selection of the training loss to the theoretical properties of the OI, which is an unbiased estimator with minimal error variance. Numerical experiments for 2D+t synthetic GP datasets demonstrate the relevance of the proposed scheme to learn computationally-efficient and scalable OI models and solvers from data. As illustrated for a real-world interpolation problems for satellite-derived geophysical dynamics, the proposed framework also extends to non-linear and multimodal interpolation problems and significantly outperforms state-of-the-art interpolation methods, when dealing with very high missing data rates.

4DVarNet-SSH: end-to-end learning of variational interpolation schemes for nadir and wide-swath satellite altimetry

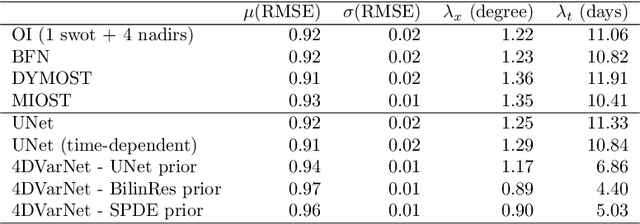
The reconstruction of sea surface currents from satellite altimeter data is a key challenge in spatial oceanography, especially with the upcoming wide-swath SWOT (Surface Ocean and Water Topography) altimeter mission. Operational systems however generally fail to retrieve mesoscale dynamics for horizontal scales below 100km and time-scale below 10 days. Here, we address this challenge through the 4DVarnet framework, an end-to-end neural scheme backed on a variational data assimilation formulation. We introduce a parametrization of the 4DVarNet scheme dedicated to the space-time interpolation of satellite altimeter data. Within an observing system simulation experiment (NATL60), we demonstrate the relevance of the proposed approach both for nadir and nadir+swot altimeter configurations for two contrasted case-study regions in terms of upper ocean dynamics. We report relative improvement with respect to the operational optimal interpolation between 30% and 60% in terms of reconstruction error. Interestingly, for the nadir+swot altimeter configuration, we reach resolved space-time scales below 70km and 7days. The code is open-source to enable reproductibility and future collaborative developments. Beyond its applicability to large-scale domains, we also address uncertainty quantification issues and generalization properties of the proposed learning setting. We discuss further future research avenues and extensions to other ocean data assimilation and space oceanography challenges.