Enhancing Surgical Documentation through Multimodal Visual-Temporal Transformers and Generative AI

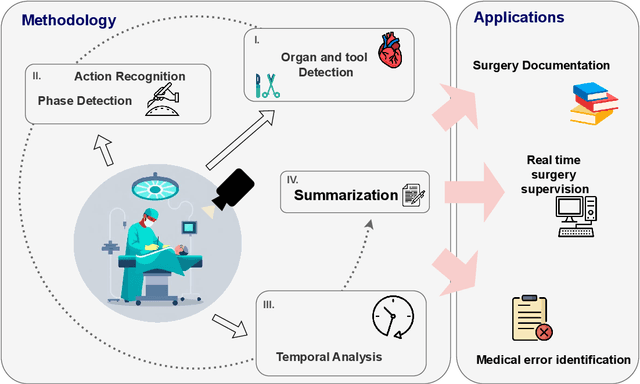
The automatic summarization of surgical videos is essential for enhancing procedural documentation, supporting surgical training, and facilitating post-operative analysis. This paper presents a novel method at the intersection of artificial intelligence and medicine, aiming to develop machine learning models with direct real-world applications in surgical contexts. We propose a multi-modal framework that leverages recent advancements in computer vision and large language models to generate comprehensive video summaries. % The approach is structured in three key stages. First, surgical videos are divided into clips, and visual features are extracted at the frame level using visual transformers. This step focuses on detecting tools, tissues, organs, and surgical actions. Second, the extracted features are transformed into frame-level captions via large language models. These are then combined with temporal features, captured using a ViViT-based encoder, to produce clip-level summaries that reflect the broader context of each video segment. Finally, the clip-level descriptions are aggregated into a full surgical report using a dedicated LLM tailored for the summarization task. % We evaluate our method on the CholecT50 dataset, using instrument and action annotations from 50 laparoscopic videos. The results show strong performance, achieving 96\% precision in tool detection and a BERT score of 0.74 for temporal context summarization. This work contributes to the advancement of AI-assisted tools for surgical reporting, offering a step toward more intelligent and reliable clinical documentation.

Neural SPDE solver for uncertainty quantification in high-dimensional space-time dynamics

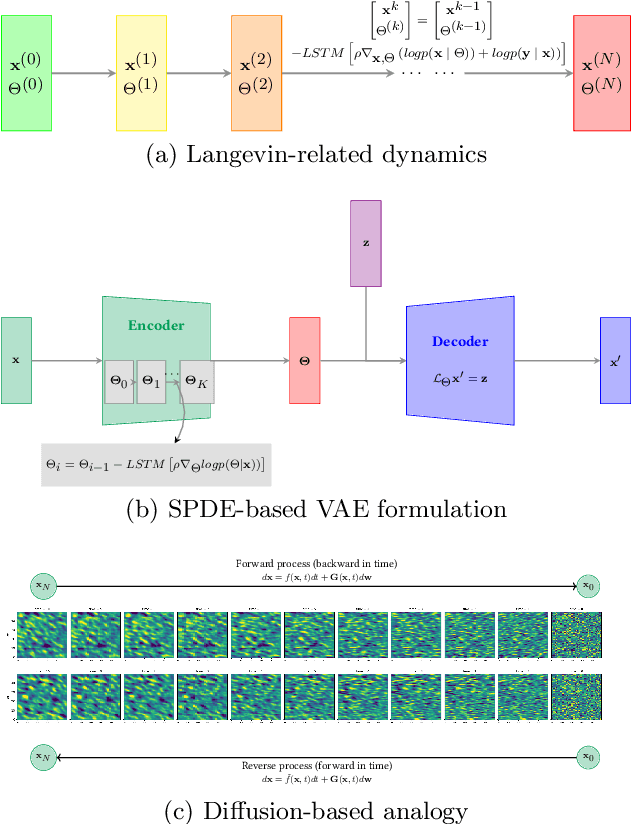
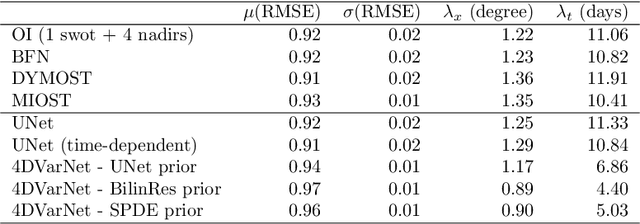
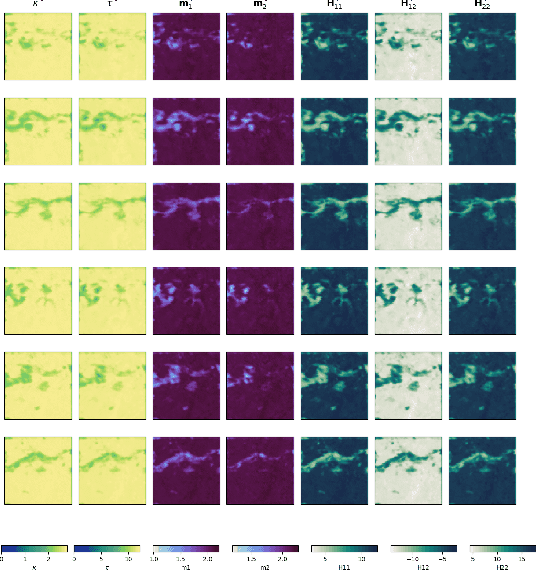
Historically, the interpolation of large geophysical datasets has been tackled using methods like Optimal Interpolation (OI) or model-based data assimilation schemes. However, the recent connection between Stochastic Partial Differential Equations (SPDE) and Gaussian Markov Random Fields (GMRF) introduced a novel approach to handle large datasets making use of sparse precision matrices in OI. Recent advancements in deep learning also addressed this issue by incorporating data assimilation into neural architectures: it treats the reconstruction task as a joint learning problem involving both prior model and solver as neural networks. Though, it requires further developments to quantify the associated uncertainties. In our work, we leverage SPDEbased Gaussian Processes to estimate complex prior models capable of handling nonstationary covariances in space and time. We develop a specific architecture able to learn both state and SPDE parameters as a neural SPDE solver, while providing the precisionbased analytical form of the SPDE sampling. The latter is used as a surrogate model along the data assimilation window. Because the prior is stochastic, we can easily draw samples from it and condition the members by our neural solver, allowing flexible estimation of the posterior distribution based on large ensemble. We demonstrate this framework on realistic Sea Surface Height datasets. Our solution improves the OI baseline, aligns with neural prior while enabling uncertainty quantification and online parameter estimation.

Learning Neural Optimal Interpolation Models and Solvers

The reconstruction of gap-free signals from observation data is a critical challenge for numerous application domains, such as geoscience and space-based earth observation, when the available sensors or the data collection processes lead to irregularly-sampled and noisy observations. Optimal interpolation (OI), also referred to as kriging, provides a theoretical framework to solve interpolation problems for Gaussian processes (GP). The associated computational complexity being rapidly intractable for n-dimensional tensors and increasing numbers of observations, a rich literature has emerged to address this issue using ensemble methods, sparse schemes or iterative approaches. Here, we introduce a neural OI scheme. It exploits a variational formulation with convolutional auto-encoders and a trainable iterative gradient-based solver. Theoretically equivalent to the OI formulation, the trainable solver asymptotically converges to the OI solution when dealing with both stationary and non-stationary linear spatio-temporal GPs. Through a bi-level optimization formulation, we relate the learning step and the selection of the training loss to the theoretical properties of the OI, which is an unbiased estimator with minimal error variance. Numerical experiments for 2D+t synthetic GP datasets demonstrate the relevance of the proposed scheme to learn computationally-efficient and scalable OI models and solvers from data. As illustrated for a real-world interpolation problems for satellite-derived geophysical dynamics, the proposed framework also extends to non-linear and multimodal interpolation problems and significantly outperforms state-of-the-art interpolation methods, when dealing with very high missing data rates.