Pascal Yiou
ESTIMR
Extreme heatwave sampling and prediction with analog Markov chain and comparisons with deep learning
Jul 18, 2023Abstract:We present a data-driven emulator, stochastic weather generator (SWG), suitable for estimating probabilities of prolonged heatwaves in France and Scandinavia. This emulator is based on the method of analogs of circulation to which we add temperature and soil moisture as predictor fields. We train the emulator on an intermediate complexity climate model run and show that it is capable of predicting conditional probabilities (forecasting) of heatwaves out of sample. Special attention is payed that this prediction is evaluated using proper score appropriate for rare events. To accelerate the computation of analogs dimensionality reduction techniques are applied and the performance is evaluated. The probabilistic prediction achieved with SWG is compared with the one achieved with Convolutional Neural Network (CNN). With the availability of hundreds of years of training data CNNs perform better at the task of probabilistic prediction. In addition, we show that the SWG emulator trained on 80 years of data is capable of estimating extreme return times of order of thousands of years for heatwaves longer than several days more precisely than the fit based on generalised extreme value distribution. Finally, the quality of its synthetic extreme teleconnection patterns obtained with stochastic weather generator is studied. We showcase two examples of such synthetic teleconnection patterns for heatwaves in France and Scandinavia that compare favorably to the very long climate model control run.
Probability distributions for analog-to-target distances
Jan 26, 2021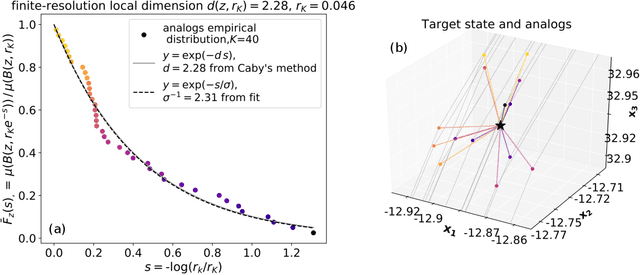
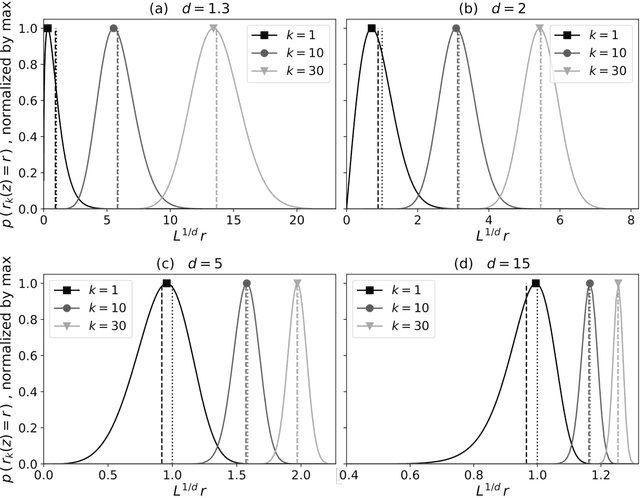


Abstract:Some properties of chaotic dynamical systems can be probed through features of recurrences, also called analogs. In practice, analogs are nearest neighbours of the state of a system, taken from a large database called the catalog. Analogs have been used in many atmospheric applications including forecasts, downscaling, predictability estimation, and attribution of extreme events. The distances of the analogs to the target state condition the performances of analog applications. These distances can be viewed as random variables, and their probability distributions can be related to the catalog size and properties of the system at stake. A few studies have focused on the first moments of return time statistics for the best analog, fixing an objective of maximum distance from this analog to the target state. However, for practical use and to reduce estimation variance, applications usually require not just one, but many analogs. In this paper, we evaluate from a theoretical standpoint and with numerical experiments the probability distributions of the $K$-best analog-to-target distances. We show that dimensionality plays a role on the size of the catalog needed to find good analogs, and also on the relative means and variances of the $K$-best analogs. Our results are based on recently developed tools from dynamical systems theory. These findings are illustrated with numerical simulations of a well-known chaotic dynamical system and on 10m-wind reanalysis data in north-west France. A practical application of our derivations for the purpose of objective-based dimension reduction is shown using the same reanalysis data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge