The impact of fine tuning in LLaMA on hallucinations for named entity extraction in legal documentation

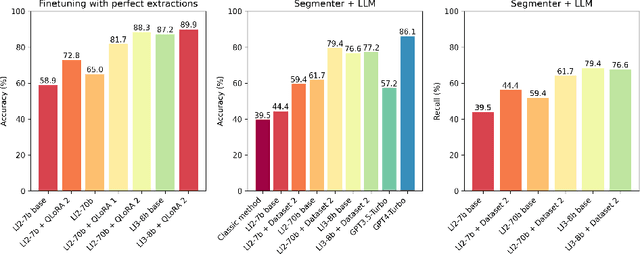
The extraction of information about traffic accidents from legal documents is crucial for quantifying insurance company costs. Extracting entities such as percentages of physical and/or psychological disability and the involved compensation amounts is a challenging process, even for experts, due to the subtle arguments and reasoning in the court decision. A two-step procedure is proposed: first, segmenting the document identifying the most relevant segments, and then extracting the entities. For text segmentation, two methodologies are compared: a classic method based on regular expressions and a second approach that divides the document into blocks of n-tokens, which are then vectorized using multilingual models for semantic searches (text-embedding-ada-002/MiniLM-L12-v2 ). Subsequently, large language models (LLaMA-2 7b, 70b, LLaMA-3 8b, and GPT-4 Turbo) are applied with prompting to the selected segments for entity extraction. For the LLaMA models, fine-tuning is performed using LoRA. LLaMA-2 7b, even with zero temperature, shows a significant number of hallucinations in extractions which are an important contention point for named entity extraction. This work shows that these hallucinations are substantially reduced after finetuning the model. The performance of the methodology based on segment vectorization and subsequent use of LLMs significantly surpasses the classic method which achieves an accuracy of 39.5%. Among open-source models, LLaMA-2 70B with finetuning achieves the highest accuracy 79.4%, surpassing its base version 61.7%. Notably, the base LLaMA-3 8B model already performs comparably to the finetuned LLaMA-2 70B model, achieving 76.6%, highlighting the rapid progress in model development. Meanwhile, GPT-4 Turbo achieves the highest accuracy at 86.1%.

Online machine-learning forecast uncertainty estimation for sequential data assimilation

Quantifying forecast uncertainty is a key aspect of state-of-the-art numerical weather prediction and data assimilation systems. Ensemble-based data assimilation systems incorporate state-dependent uncertainty quantification based on multiple model integrations. However, this approach is demanding in terms of computations and development. In this work a machine learning method is presented based on convolutional neural networks that estimates the state-dependent forecast uncertainty represented by the forecast error covariance matrix using a single dynamical model integration. This is achieved by the use of a loss function that takes into account the fact that the forecast errors are heterodastic. The performance of this approach is examined within a hybrid data assimilation method that combines a Kalman-like analysis update and the machine learning based estimation of a state-dependent forecast error covariance matrix. Observing system simulation experiments are conducted using the Lorenz'96 model as a proof-of-concept. The promising results show that the machine learning method is able to predict precise values of the forecast covariance matrix in relatively high-dimensional states. Moreover, the hybrid data assimilation method shows similar performance to the ensemble Kalman filter outperforming it when the ensembles are relatively small.

Evaluation of Machine Learning Techniques for Forecast Uncertainty Quantification

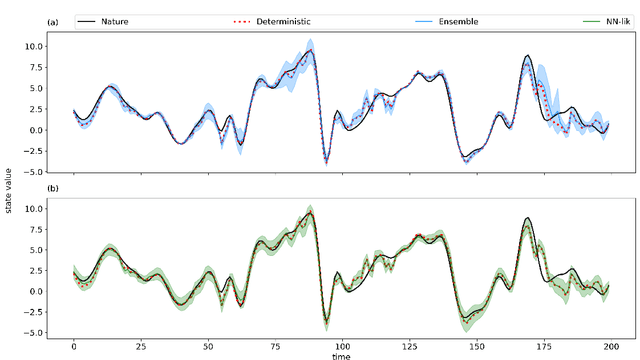
Producing an accurate weather forecast and a reliable quantification of its uncertainty is an open scientific challenge. Ensemble forecasting is, so far, the most successful approach to produce relevant forecasts along with an estimation of their uncertainty. The main limitations of ensemble forecasting are the high computational cost and the difficulty to capture and quantify different sources of uncertainty, particularly those associated with model errors. In this work proof-of-concept model experiments are conducted to examine the performance of ANNs trained to predict a corrected state of the system and the state uncertainty using only a single deterministic forecast as input. We compare different training strategies: one based on a direct training using the mean and spread of an ensemble forecast as target, the other ones rely on an indirect training strategy using a deterministic forecast as target in which the uncertainty is implicitly learned from the data. For the last approach two alternative loss functions are proposed and evaluated, one based on the data observation likelihood and the other one based on a local estimation of the error. The performance of the networks is examined at different lead times and in scenarios with and without model errors. Experiments using the Lorenz'96 model show that the ANNs are able to emulate some of the properties of ensemble forecasts like the filtering of the most unpredictable modes and a state-dependent quantification of the forecast uncertainty. Moreover, ANNs provide a reliable estimation of the forecast uncertainty in the presence of model error.

Kernel embedded nonlinear observational mappings in the variational mapping particle filter

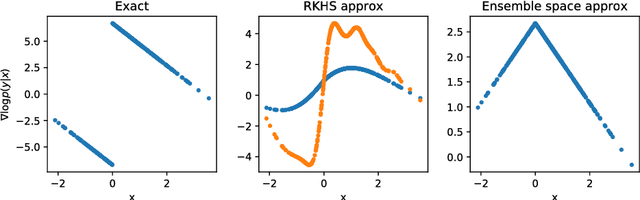
Recently, some works have suggested methods to combine variational probabilistic inference with Monte Carlo sampling. One promising approach is via local optimal transport. In this approach, a gradient steepest descent method based on local optimal transport principles is formulated to transform deterministically point samples from an intermediate density to a posterior density. The local mappings that transform the intermediate densities are embedded in a reproducing kernel Hilbert space (RKHS). This variational mapping method requires the evaluation of the log-posterior density gradient and therefore the adjoint of the observational operator. In this work, we evaluate nonlinear observational mappings in the variational mapping method using two approximations that avoid the adjoint, an ensemble based approximation in which the gradient is approximated by the particle covariances in the state and observational spaces the so-called ensemble space and an RKHS approximation in which the observational mapping is embedded in an RKHS and the gradient is derived there. The approximations are evaluated for highly nonlinear observational operators and in a low-dimensional chaotic dynamical system. The RKHS approximation is shown to be highly successful and superior to the ensemble approximation.

Kernel embedding of maps for sequential Bayesian inference: The variational mapping particle filter

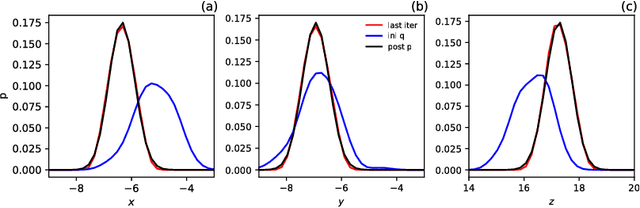
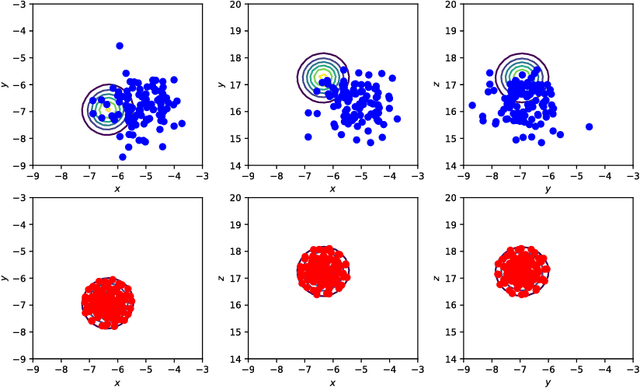
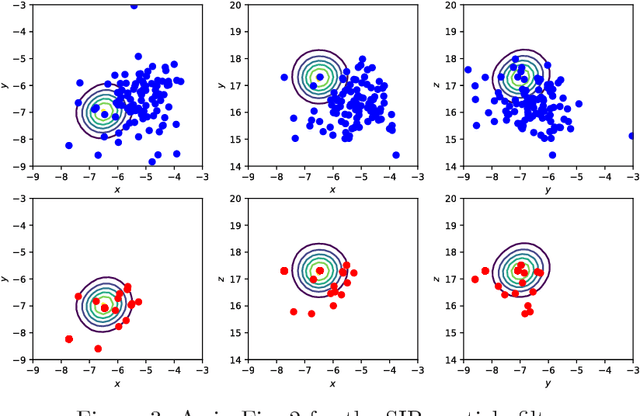
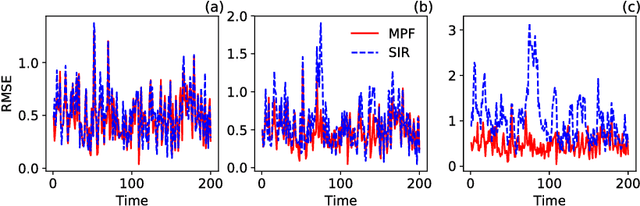
In this work, a novel sequential Monte Carlo filter is introduced which aims at efficient sampling of high-dimensional state spaces with a limited number of particles. Particles are pushed forward from the prior to the posterior density using a sequence of mappings that minimizes the Kullback-Leibler divergence between the posterior and the sequence of intermediate densities. The sequence of mappings represents a gradient flow. A key ingredient of the mappings is that they are embedded in a reproducing kernel Hilbert space, which allows for a practical and efficient algorithm. The embedding provides a direct means to calculate the gradient of the Kullback-Leibler divergence leading to quick convergence using well-known gradient-based stochastic optimization algorithms. Evaluation of the method is conducted in the chaotic Lorenz-63 system, the Lorenz-96 system, which is a coarse prototype of atmospheric dynamics, and an epidemic model that describes cholera dynamics. No resampling is required in the mapping particle filter even for long recursive sequences. The number of effective particles remains close to the total number of particles in all the experiments.