Kernel embedded nonlinear observational mappings in the variational mapping particle filter
Paper and Code
Jan 29, 2019
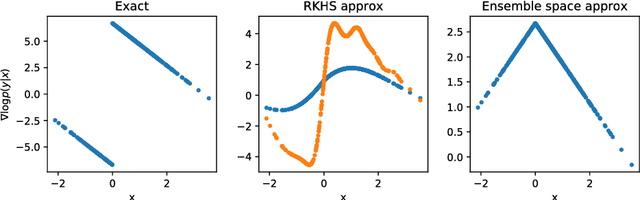


Recently, some works have suggested methods to combine variational probabilistic inference with Monte Carlo sampling. One promising approach is via local optimal transport. In this approach, a gradient steepest descent method based on local optimal transport principles is formulated to transform deterministically point samples from an intermediate density to a posterior density. The local mappings that transform the intermediate densities are embedded in a reproducing kernel Hilbert space (RKHS). This variational mapping method requires the evaluation of the log-posterior density gradient and therefore the adjoint of the observational operator. In this work, we evaluate nonlinear observational mappings in the variational mapping method using two approximations that avoid the adjoint, an ensemble based approximation in which the gradient is approximated by the particle covariances in the state and observational spaces the so-called ensemble space and an RKHS approximation in which the observational mapping is embedded in an RKHS and the gradient is derived there. The approximations are evaluated for highly nonlinear observational operators and in a low-dimensional chaotic dynamical system. The RKHS approximation is shown to be highly successful and superior to the ensemble approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge