Kernel embedded nonlinear observational mappings in the variational mapping particle filter

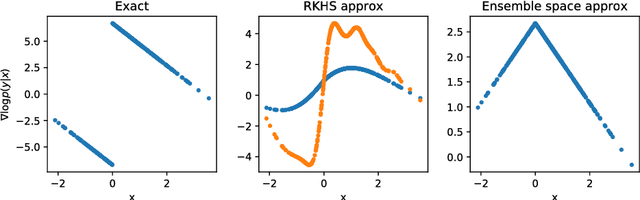
Recently, some works have suggested methods to combine variational probabilistic inference with Monte Carlo sampling. One promising approach is via local optimal transport. In this approach, a gradient steepest descent method based on local optimal transport principles is formulated to transform deterministically point samples from an intermediate density to a posterior density. The local mappings that transform the intermediate densities are embedded in a reproducing kernel Hilbert space (RKHS). This variational mapping method requires the evaluation of the log-posterior density gradient and therefore the adjoint of the observational operator. In this work, we evaluate nonlinear observational mappings in the variational mapping method using two approximations that avoid the adjoint, an ensemble based approximation in which the gradient is approximated by the particle covariances in the state and observational spaces the so-called ensemble space and an RKHS approximation in which the observational mapping is embedded in an RKHS and the gradient is derived there. The approximations are evaluated for highly nonlinear observational operators and in a low-dimensional chaotic dynamical system. The RKHS approximation is shown to be highly successful and superior to the ensemble approximation.

Kernel embedding of maps for sequential Bayesian inference: The variational mapping particle filter

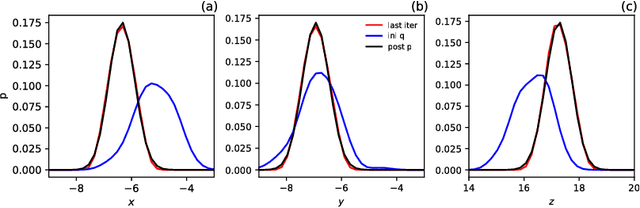
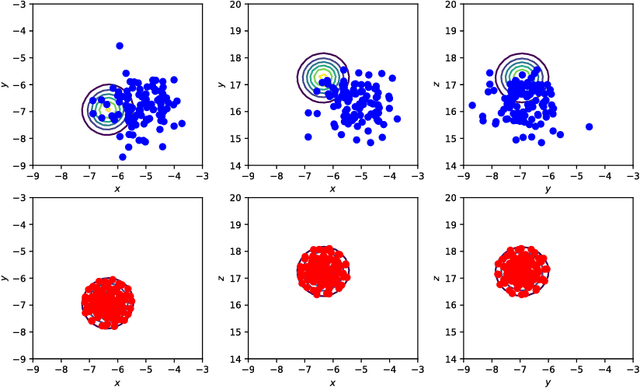
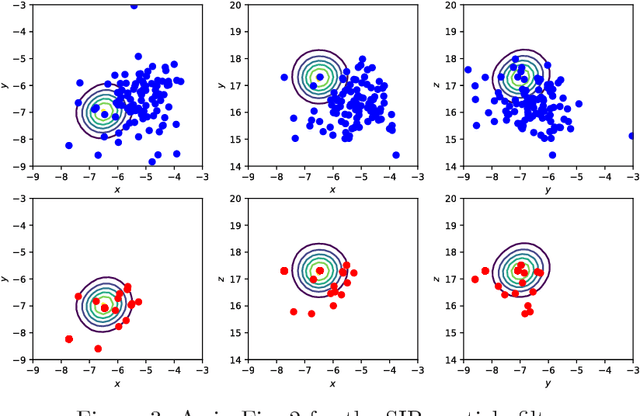
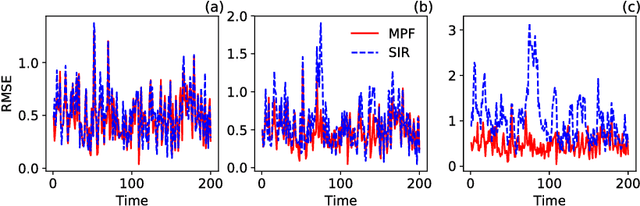
In this work, a novel sequential Monte Carlo filter is introduced which aims at efficient sampling of high-dimensional state spaces with a limited number of particles. Particles are pushed forward from the prior to the posterior density using a sequence of mappings that minimizes the Kullback-Leibler divergence between the posterior and the sequence of intermediate densities. The sequence of mappings represents a gradient flow. A key ingredient of the mappings is that they are embedded in a reproducing kernel Hilbert space, which allows for a practical and efficient algorithm. The embedding provides a direct means to calculate the gradient of the Kullback-Leibler divergence leading to quick convergence using well-known gradient-based stochastic optimization algorithms. Evaluation of the method is conducted in the chaotic Lorenz-63 system, the Lorenz-96 system, which is a coarse prototype of atmospheric dynamics, and an epidemic model that describes cholera dynamics. No resampling is required in the mapping particle filter even for long recursive sequences. The number of effective particles remains close to the total number of particles in all the experiments.