Online machine-learning forecast uncertainty estimation for sequential data assimilation

Quantifying forecast uncertainty is a key aspect of state-of-the-art numerical weather prediction and data assimilation systems. Ensemble-based data assimilation systems incorporate state-dependent uncertainty quantification based on multiple model integrations. However, this approach is demanding in terms of computations and development. In this work a machine learning method is presented based on convolutional neural networks that estimates the state-dependent forecast uncertainty represented by the forecast error covariance matrix using a single dynamical model integration. This is achieved by the use of a loss function that takes into account the fact that the forecast errors are heterodastic. The performance of this approach is examined within a hybrid data assimilation method that combines a Kalman-like analysis update and the machine learning based estimation of a state-dependent forecast error covariance matrix. Observing system simulation experiments are conducted using the Lorenz'96 model as a proof-of-concept. The promising results show that the machine learning method is able to predict precise values of the forecast covariance matrix in relatively high-dimensional states. Moreover, the hybrid data assimilation method shows similar performance to the ensemble Kalman filter outperforming it when the ensembles are relatively small.

Evaluation of Machine Learning Techniques for Forecast Uncertainty Quantification

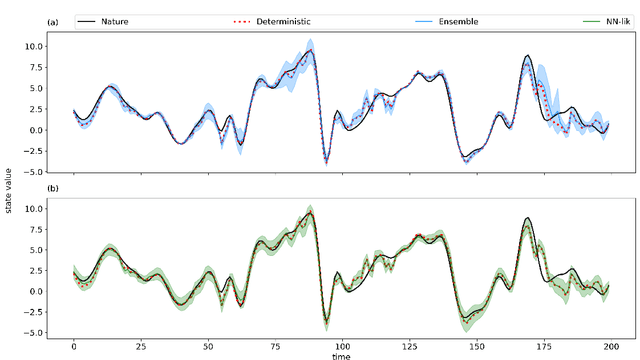
Producing an accurate weather forecast and a reliable quantification of its uncertainty is an open scientific challenge. Ensemble forecasting is, so far, the most successful approach to produce relevant forecasts along with an estimation of their uncertainty. The main limitations of ensemble forecasting are the high computational cost and the difficulty to capture and quantify different sources of uncertainty, particularly those associated with model errors. In this work proof-of-concept model experiments are conducted to examine the performance of ANNs trained to predict a corrected state of the system and the state uncertainty using only a single deterministic forecast as input. We compare different training strategies: one based on a direct training using the mean and spread of an ensemble forecast as target, the other ones rely on an indirect training strategy using a deterministic forecast as target in which the uncertainty is implicitly learned from the data. For the last approach two alternative loss functions are proposed and evaluated, one based on the data observation likelihood and the other one based on a local estimation of the error. The performance of the networks is examined at different lead times and in scenarios with and without model errors. Experiments using the Lorenz'96 model show that the ANNs are able to emulate some of the properties of ensemble forecasts like the filtering of the most unpredictable modes and a state-dependent quantification of the forecast uncertainty. Moreover, ANNs provide a reliable estimation of the forecast uncertainty in the presence of model error.