Cauchy-Schwarz Divergence Information Bottleneck for Regression

The information bottleneck (IB) approach is popular to improve the generalization, robustness and explainability of deep neural networks. Essentially, it aims to find a minimum sufficient representation $\mathbf{t}$ by striking a trade-off between a compression term $I(\mathbf{x};\mathbf{t})$ and a prediction term $I(y;\mathbf{t})$, where $I(\cdot;\cdot)$ refers to the mutual information (MI). MI is for the IB for the most part expressed in terms of the Kullback-Leibler (KL) divergence, which in the regression case corresponds to prediction based on mean squared error (MSE) loss with Gaussian assumption and compression approximated by variational inference. In this paper, we study the IB principle for the regression problem and develop a new way to parameterize the IB with deep neural networks by exploiting favorable properties of the Cauchy-Schwarz (CS) divergence. By doing so, we move away from MSE-based regression and ease estimation by avoiding variational approximations or distributional assumptions. We investigate the improved generalization ability of our proposed CS-IB and demonstrate strong adversarial robustness guarantees. We demonstrate its superior performance on six real-world regression tasks over other popular deep IB approaches. We additionally observe that the solutions discovered by CS-IB always achieve the best trade-off between prediction accuracy and compression ratio in the information plane. The code is available at \url{https://github.com/SJYuCNEL/Cauchy-Schwarz-Information-Bottleneck}.

On the Effects of Self-supervision and Contrastive Alignment in Deep Multi-view Clustering

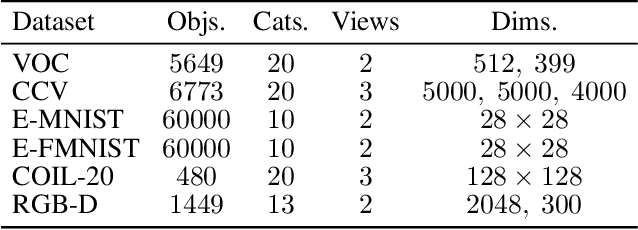
Self-supervised learning is a central component in recent approaches to deep multi-view clustering (MVC). However, we find large variations in the development of self-supervision-based methods for deep MVC, potentially slowing the progress of the field. To address this, we present DeepMVC, a unified framework for deep MVC that includes many recent methods as instances. We leverage our framework to make key observations about the effect of self-supervision, and in particular, drawbacks of aligning representations with contrastive learning. Further, we prove that contrastive alignment can negatively influence cluster separability, and that this effect becomes worse when the number of views increases. Motivated by our findings, we develop several new DeepMVC instances with new forms of self-supervision. We conduct extensive experiments and find that (i) in line with our theoretical findings, contrastive alignments decreases performance on datasets with many views; (ii) all methods benefit from some form of self-supervision; and (iii) our new instances outperform previous methods on several datasets. Based on our results, we suggest several promising directions for future research. To enhance the openness of the field, we provide an open-source implementation of DeepMVC, including recent models and our new instances. Our implementation includes a consistent evaluation protocol, facilitating fair and accurate evaluation of methods and components.

Hubs and Hyperspheres: Reducing Hubness and Improving Transductive Few-shot Learning with Hyperspherical Embeddings

Distance-based classification is frequently used in transductive few-shot learning (FSL). However, due to the high-dimensionality of image representations, FSL classifiers are prone to suffer from the hubness problem, where a few points (hubs) occur frequently in multiple nearest neighbour lists of other points. Hubness negatively impacts distance-based classification when hubs from one class appear often among the nearest neighbors of points from another class, degrading the classifier's performance. To address the hubness problem in FSL, we first prove that hubness can be eliminated by distributing representations uniformly on the hypersphere. We then propose two new approaches to embed representations on the hypersphere, which we prove optimize a tradeoff between uniformity and local similarity preservation -- reducing hubness while retaining class structure. Our experiments show that the proposed methods reduce hubness, and significantly improves transductive FSL accuracy for a wide range of classifiers.

The Conditional Cauchy-Schwarz Divergence with Applications to Time-Series Data and Sequential Decision Making

The Cauchy-Schwarz (CS) divergence was developed by Pr\'{i}ncipe et al. in 2000. In this paper, we extend the classic CS divergence to quantify the closeness between two conditional distributions and show that the developed conditional CS divergence can be simply estimated by a kernel density estimator from given samples. We illustrate the advantages (e.g., the rigorous faithfulness guarantee, the lower computational complexity, the higher statistical power, and the much more flexibility in a wide range of applications) of our conditional CS divergence over previous proposals, such as the conditional KL divergence and the conditional maximum mean discrepancy. We also demonstrate the compelling performance of conditional CS divergence in two machine learning tasks related to time series data and sequential inference, namely the time series clustering and the uncertainty-guided exploration for sequential decision making.

The Kernelized Taylor Diagram

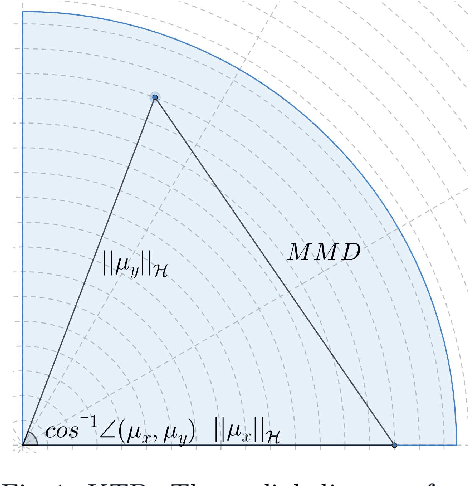
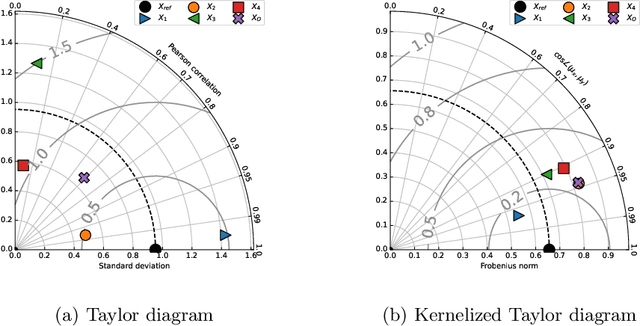
This paper presents the kernelized Taylor diagram, a graphical framework for visualizing similarities between data populations. The kernelized Taylor diagram builds on the widely used Taylor diagram, which is used to visualize similarities between populations. However, the Taylor diagram has several limitations such as not capturing non-linear relationships and sensitivity to outliers. To address such limitations, we propose the kernelized Taylor diagram. Our proposed kernelized Taylor diagram is capable of visualizing similarities between populations with minimal assumptions of the data distributions. The kernelized Taylor diagram relates the maximum mean discrepancy and the kernel mean embedding in a single diagram, a construction that, to the best of our knowledge, have not been devised prior to this work. We believe that the kernelized Taylor diagram can be a valuable tool in data visualization.

RELAX: Representation Learning Explainability

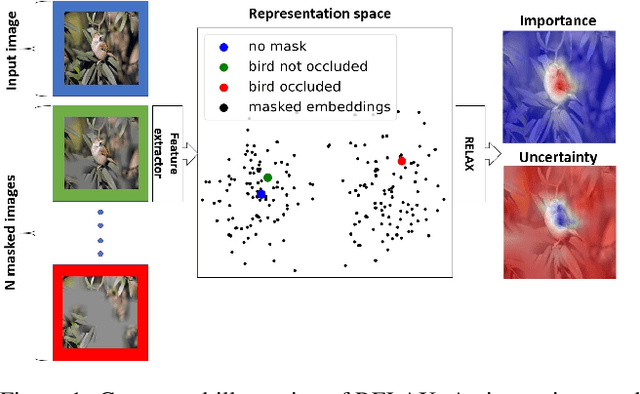
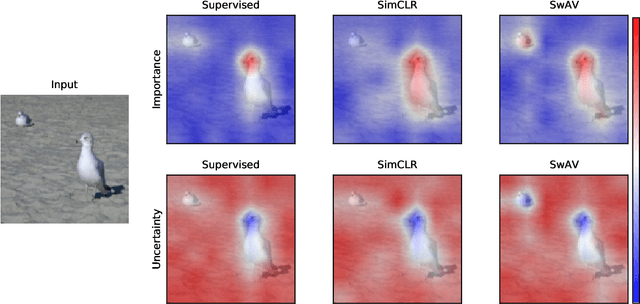
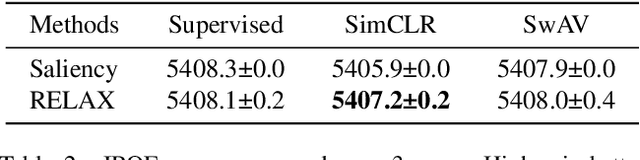
Despite the significant improvements that representation learning via self-supervision has led to when learning from unlabeled data, no methods exist that explain what influences the learned representation. We address this need through our proposed approach, RELAX, which is the first approach for attribution-based explanations of representations. Our approach can also model the uncertainty in its explanations, which is essential to produce trustworthy explanations. RELAX explains representations by measuring similarities in the representation space between an input and masked out versions of itself, providing intuitive explanations and significantly outperforming the gradient-based baseline. We provide theoretical interpretations of RELAX and conduct a novel analysis of feature extractors trained using supervised and unsupervised learning, providing insights into different learning strategies. Finally, we illustrate the usability of RELAX in multi-view clustering and highlight that incorporating uncertainty can be essential for providing low-complexity explanations, taking a crucial step towards explaining representations.

Reconsidering Representation Alignment for Multi-view Clustering

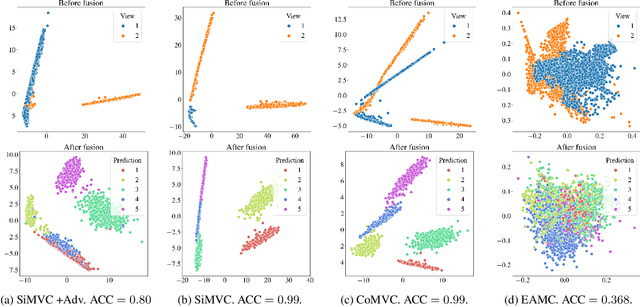
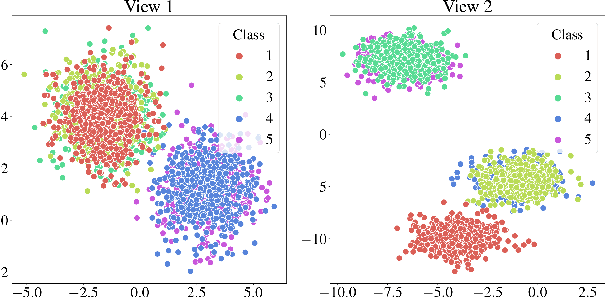
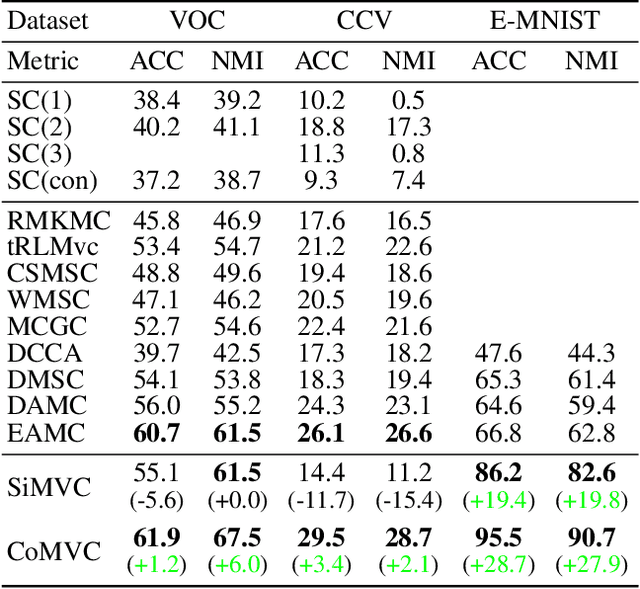
Aligning distributions of view representations is a core component of today's state of the art models for deep multi-view clustering. However, we identify several drawbacks with na\"ively aligning representation distributions. We demonstrate that these drawbacks both lead to less separable clusters in the representation space, and inhibit the model's ability to prioritize views. Based on these observations, we develop a simple baseline model for deep multi-view clustering. Our baseline model avoids representation alignment altogether, while performing similar to, or better than, the current state of the art. We also expand our baseline model by adding a contrastive learning component. This introduces a selective alignment procedure that preserves the model's ability to prioritize views. Our experiments show that the contrastive learning component enhances the baseline model, improving on the current state of the art by a large margin on several datasets.

Information Plane Analysis of Deep Neural Networks via Matrix-Based Renyi's Entropy and Tensor Kernels

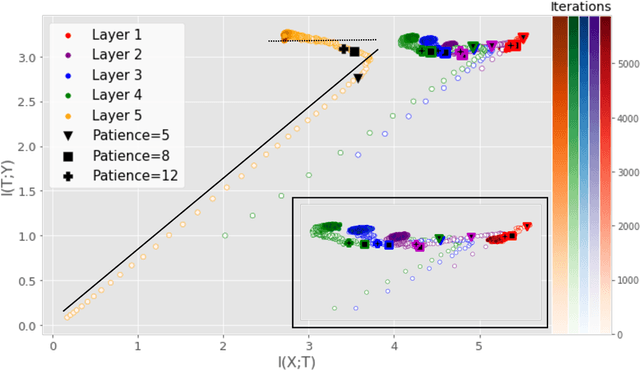
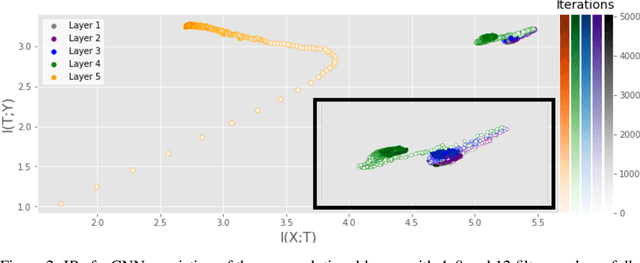
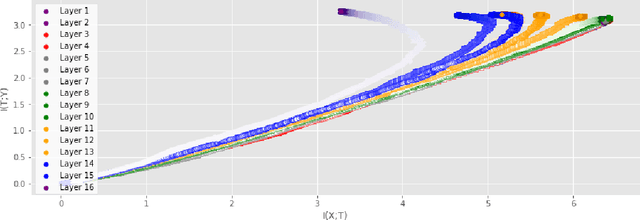
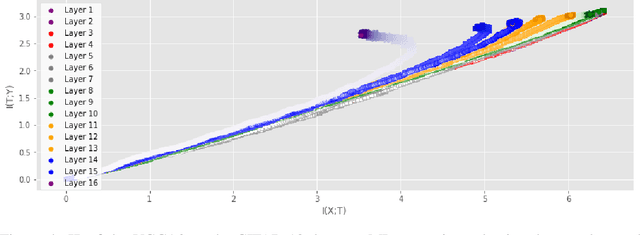
Analyzing deep neural networks (DNNs) via information plane (IP) theory has gained tremendous attention recently as a tool to gain insight into, among others, their generalization ability. However, it is by no means obvious how to estimate mutual information (MI) between each hidden layer and the input/desired output, to construct the IP. For instance, hidden layers with many neurons require MI estimators with robustness towards the high dimensionality associated with such layers. MI estimators should also be able to naturally handle convolutional layers, while at the same time being computationally tractable to scale to large networks. None of the existing IP methods to date have been able to study truly deep Convolutional Neural Networks (CNNs), such as the e.g.\ VGG-16. In this paper, we propose an IP analysis using the new matrix--based R\'enyi's entropy coupled with tensor kernels over convolutional layers, leveraging the power of kernel methods to represent properties of the probability distribution independently of the dimensionality of the data. The obtained results shed new light on the previous literature concerning small-scale DNNs, however using a completely new approach. Importantly, the new framework enables us to provide the first comprehensive IP analysis of contemporary large-scale DNNs and CNNs, investigating the different training phases and providing new insights into the training dynamics of large-scale neural networks.

Deep Divergence-Based Approach to Clustering

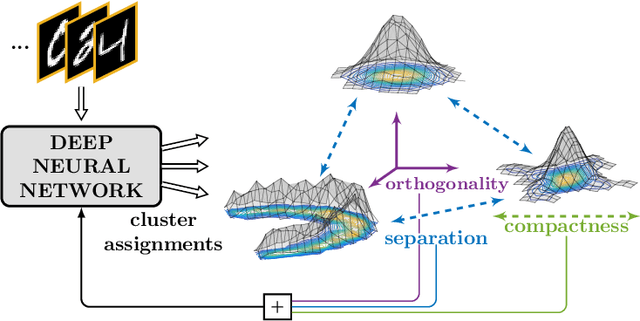
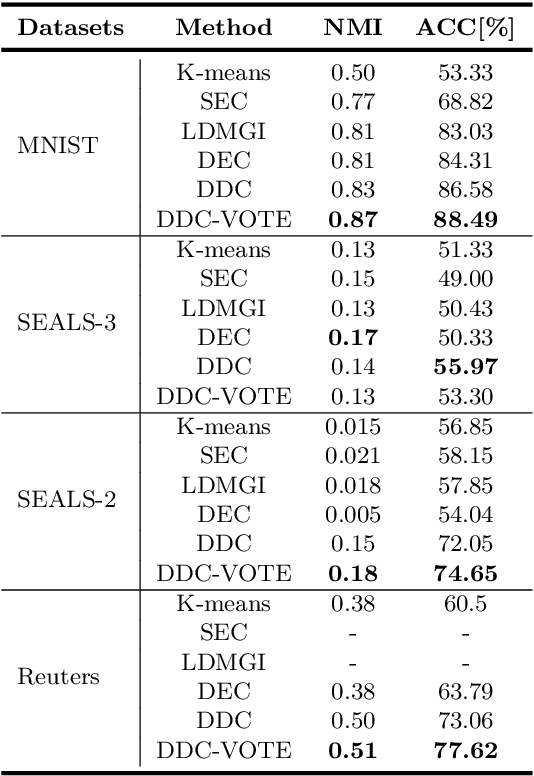
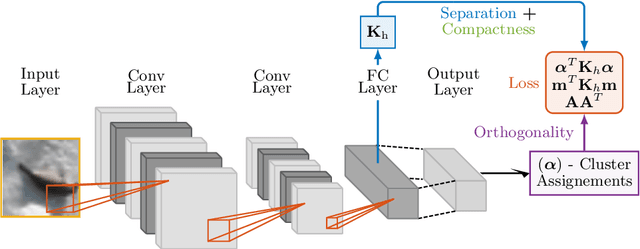
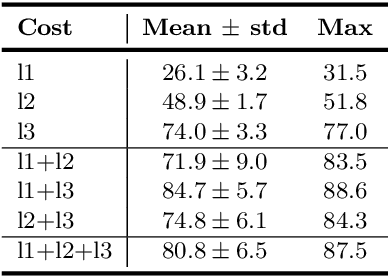
A promising direction in deep learning research consists in learning representations and simultaneously discovering cluster structure in unlabeled data by optimizing a discriminative loss function. As opposed to supervised deep learning, this line of research is in its infancy, and how to design and optimize suitable loss functions to train deep neural networks for clustering is still an open question. Our contribution to this emerging field is a new deep clustering network that leverages the discriminative power of information-theoretic divergence measures, which have been shown to be effective in traditional clustering. We propose a novel loss function that incorporates geometric regularization constraints, thus avoiding degenerate structures of the resulting clustering partition. Experiments on synthetic benchmarks and real datasets show that the proposed network achieves competitive performance with respect to other state-of-the-art methods, scales well to large datasets, and does not require pre-training steps.

Reservoir computing approaches for representation and classification of multivariate time series

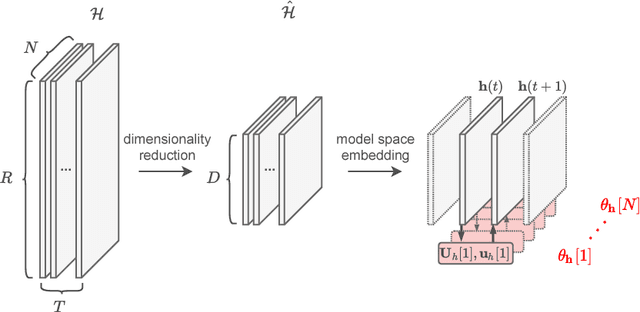
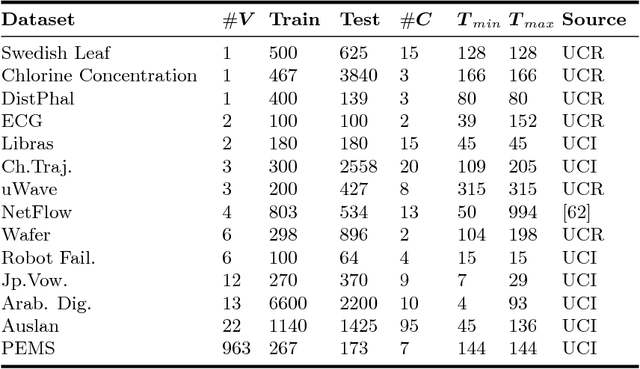
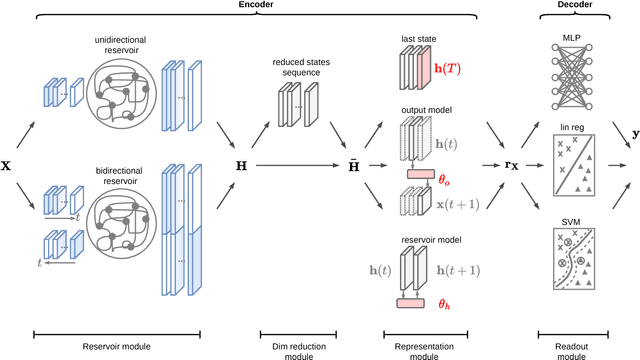
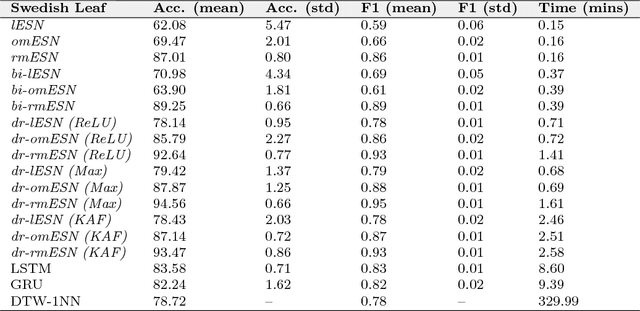
Classification of multivariate time series (MTS) has been tackled with a large variety of methodologies and applied to a wide range of scenarios. Among the existing approaches, reservoir computing (RC) techniques, which implement a fixed and high-dimensional recurrent network to process sequential data, are computationally efficient tools to generate a vectorial, fixed-size representation of the MTS that can be further processed by standard classifiers. Despite their unrivaled training speed, MTS classifiers based on a standard RC architecture fail to achieve the same accuracy of other classifiers, such as those exploiting fully trainable recurrent networks. In this paper we introduce the reservoir model space, an RC approach to learn vectorial representations of MTS in an unsupervised fashion. Each MTS is encoded within the parameters of a linear model trained to predict a low-dimensional embedding of the reservoir dynamics. Our model space yields a powerful representation of the MTS and, thanks to an intermediate dimensionality reduction procedure, attains computational performance comparable to other RC methods. As a second contribution we propose a modular RC framework for MTS classification, with an associated open source Python library. By combining the different modules it is possible to seamlessly implement advanced RC architectures, including our proposed unsupervised representation, bidirectional reservoirs, and non-linear readouts, such as deep neural networks with both fixed and flexible activation functions. Results obtained on benchmark and real-world MTS datasets show that RC classifiers are dramatically faster and, when implemented using our proposed representation, also achieve superior classification accuracy.