Kernel Operator-Theoretic Bayesian Filter for Nonlinear Dynamical Systems

Motivated by the surge of interest in Koopman operator theory, we propose a machine-learning alternative based on a functional Bayesian perspective for operator-theoretic modeling of unknown, data-driven, nonlinear dynamical systems. This formulation is directly done in an infinite-dimensional space of linear operators or Hilbert space with universal approximation property. The theory of reproducing kernel Hilbert space (RKHS) allows the lifting of nonlinear dynamics to a potentially infinite-dimensional space via linear embeddings, where a general nonlinear function is represented as a set of linear functions or operators in the functional space. This allows us to apply classical linear Bayesian methods such as the Kalman filter directly in the Hilbert space, yielding nonlinear solutions in the original input space. This kernel perspective on the Koopman operator offers two compelling advantages. First, the Hilbert space can be constructed deterministically, agnostic to the nonlinear dynamics. The Gaussian kernel is universal, approximating uniformly an arbitrary continuous target function over any compact domain. Second, Bayesian filter is an adaptive, linear minimum-variance algorithm, allowing the system to update the Koopman operator and continuously track the changes across an extended period of time, ideally suited for modern data-driven applications such as real-time machine learning using streaming data. In this paper, we present several practical implementations to obtain a finite-dimensional approximation of the functional Bayesian filter (FBF). Due to the rapid decay of the Gaussian kernel, excellent approximation is obtained with a small dimension. We demonstrate that this practical approach can obtain accurate results and outperform finite-dimensional Koopman decomposition.

Feature Learning in Image Hierarchies using Functional Maximal Correlation

This paper proposes the Hierarchical Functional Maximal Correlation Algorithm (HFMCA), a hierarchical methodology that characterizes dependencies across two hierarchical levels in multiview systems. By framing view similarities as dependencies and ensuring contrastivity by imposing orthonormality, HFMCA achieves faster convergence and increased stability in self-supervised learning. HFMCA defines and measures dependencies within image hierarchies, from pixels and patches to full images. We find that the network topology for approximating orthonormal basis functions aligns with a vanilla CNN, enabling the decomposition of density ratios between neighboring layers of feature maps. This approach provides powerful interpretability, revealing the resemblance between supervision and self-supervision through the lens of internal representations.

The Conditional Cauchy-Schwarz Divergence with Applications to Time-Series Data and Sequential Decision Making

The Cauchy-Schwarz (CS) divergence was developed by Pr\'{i}ncipe et al. in 2000. In this paper, we extend the classic CS divergence to quantify the closeness between two conditional distributions and show that the developed conditional CS divergence can be simply estimated by a kernel density estimator from given samples. We illustrate the advantages (e.g., the rigorous faithfulness guarantee, the lower computational complexity, the higher statistical power, and the much more flexibility in a wide range of applications) of our conditional CS divergence over previous proposals, such as the conditional KL divergence and the conditional maximum mean discrepancy. We also demonstrate the compelling performance of conditional CS divergence in two machine learning tasks related to time series data and sequential inference, namely the time series clustering and the uncertainty-guided exploration for sequential decision making.

Concept Drift Detection and Adaptation with Hierarchical Hypothesis Testing

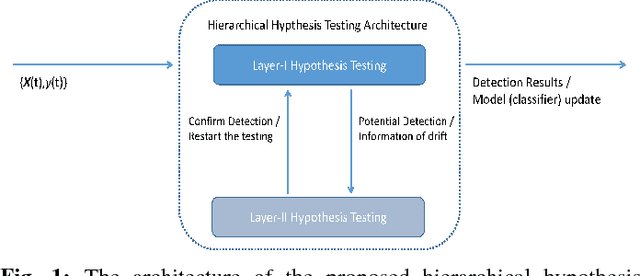
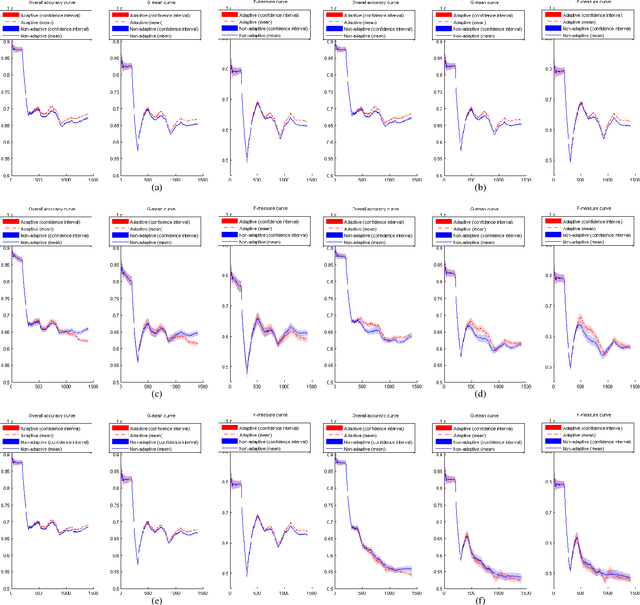
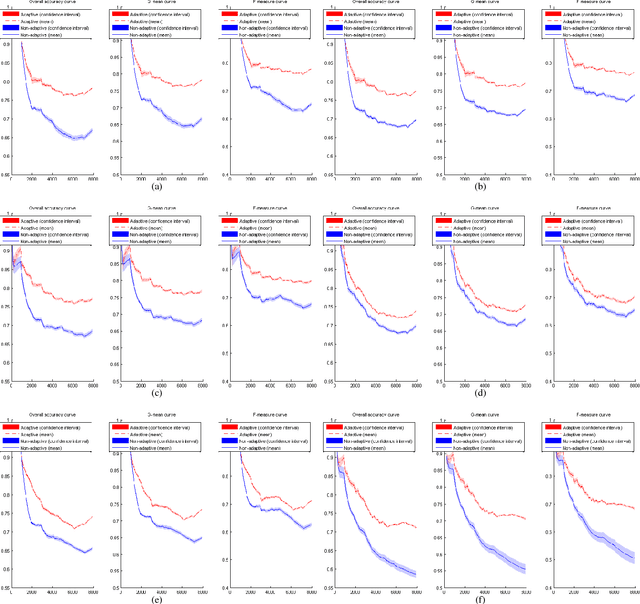
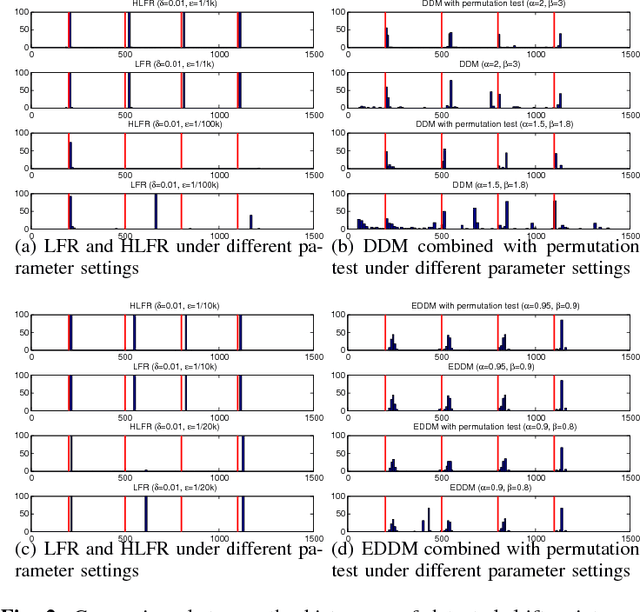
A fundamental issue for statistical classification models in a streaming environment is that the joint distribution between predictor and response variables changes over time (a phenomenon also known as concept drifts), such that their classification performance deteriorates dramatically. In this paper, we first present a hierarchical hypothesis testing (HHT) framework that can detect and also adapt to various concept drift types (e.g., recurrent or irregular, gradual or abrupt), even in the presence of imbalanced data labels. A novel concept drift detector, namely Hierarchical Linear Four Rates (HLFR), is implemented under the HHT framework thereafter. By substituting a widely-acknowledged retraining scheme with an adaptive training strategy, we further demonstrate that the concept drift adaptation capability of HLFR can be significantly boosted. The theoretical analysis on the Type-I and Type-II errors of HLFR is also performed. Experiments on both simulated and real-world datasets illustrate that our methods outperform state-of-the-art methods in terms of detection precision, detection delay as well as the adaptability across different concept drift types.

Maximum Correntropy Kalman Filter

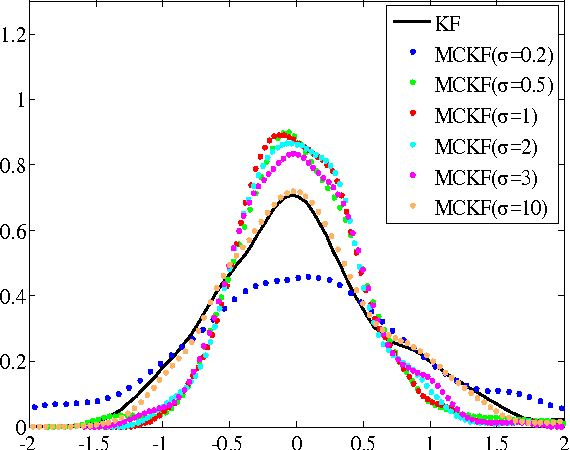
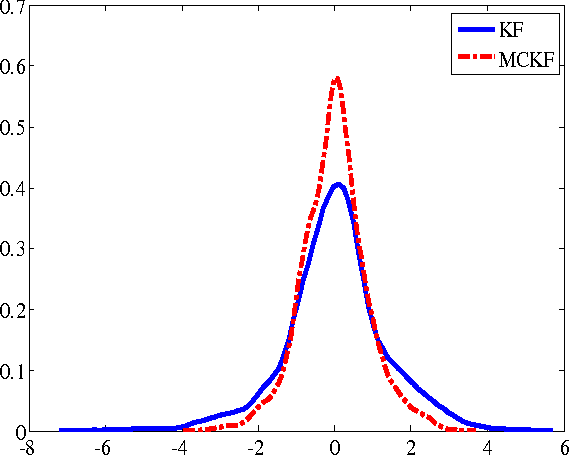
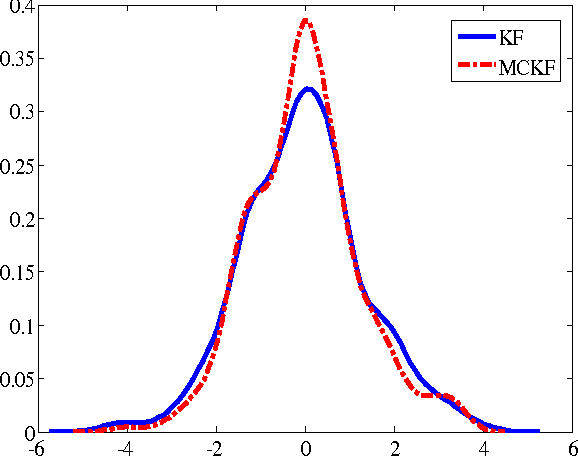
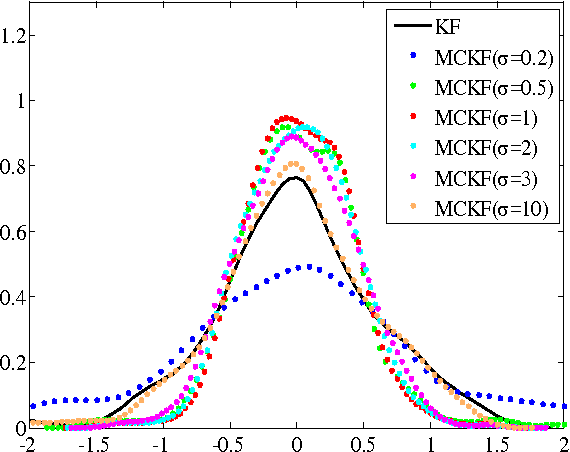
Traditional Kalman filter (KF) is derived under the well-known minimum mean square error (MMSE) criterion, which is optimal under Gaussian assumption. However, when the signals are non-Gaussian, especially when the system is disturbed by some heavy-tailed impulsive noises, the performance of KF will deteriorate seriously. To improve the robustness of KF against impulsive noises, we propose in this work a new Kalman filter, called the maximum correntropy Kalman filter (MCKF), which adopts the robust maximum correntropy criterion (MCC) as the optimality criterion, instead of using the MMSE. Similar to the traditional KF, the state mean and covariance matrix propagation equations are used to give prior estimations of the state and covariance matrix in MCKF. A novel fixed-point algorithm is then used to update the posterior estimations. A sufficient condition that guarantees the convergence of the fixed-point algorithm is given. Illustration examples are presented to demonstrate the effectiveness and robustness of the new algorithm.

Generalized Correntropy for Robust Adaptive Filtering

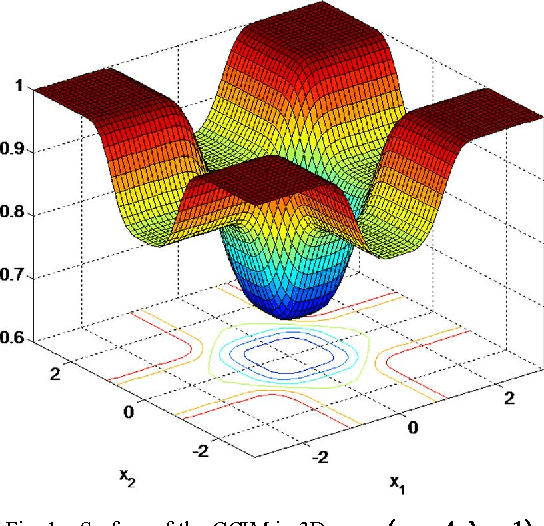
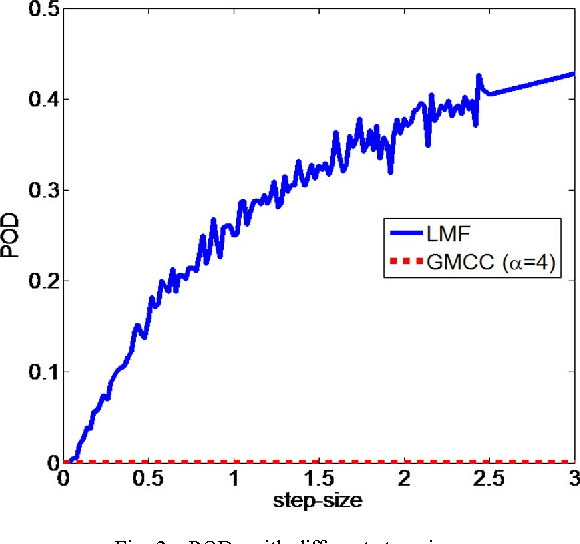
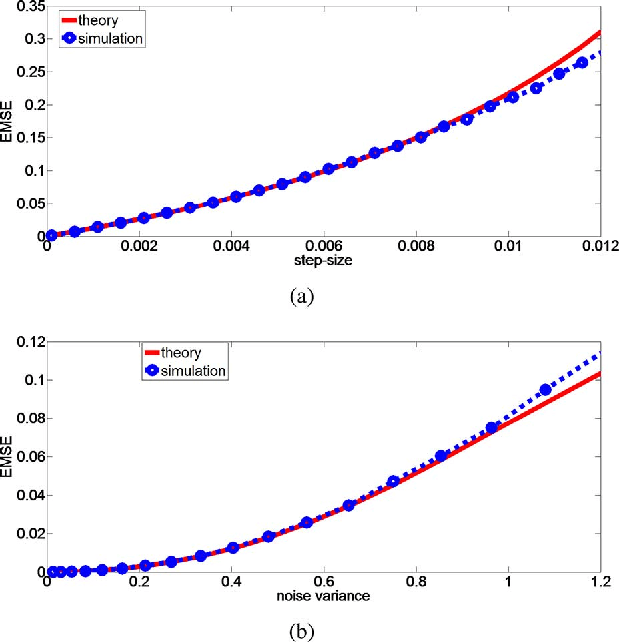
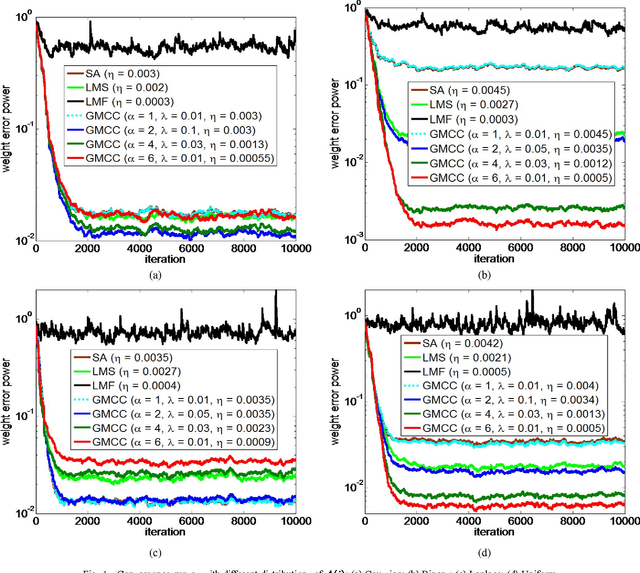
As a robust nonlinear similarity measure in kernel space, correntropy has received increasing attention in domains of machine learning and signal processing. In particular, the maximum correntropy criterion (MCC) has recently been successfully applied in robust regression and filtering. The default kernel function in correntropy is the Gaussian kernel, which is, of course, not always the best choice. In this work, we propose a generalized correntropy that adopts the generalized Gaussian density (GGD) function as the kernel (not necessarily a Mercer kernel), and present some important properties. We further propose the generalized maximum correntropy criterion (GMCC), and apply it to adaptive filtering. An adaptive algorithm, called the GMCC algorithm, is derived, and the mean square convergence performance is studied. We show that the proposed algorithm is very stable and can achieve zero probability of divergence (POD). Simulation results confirm the theoretical expectations and demonstrate the desirable performance of the new algorithm.