ELEMENT: Episodic and Lifelong Exploration via Maximum Entropy

This paper proposes \emph{Episodic and Lifelong Exploration via Maximum ENTropy} (ELEMENT), a novel, multiscale, intrinsically motivated reinforcement learning (RL) framework that is able to explore environments without using any extrinsic reward and transfer effectively the learned skills to downstream tasks. We advance the state of the art in three ways. First, we propose a multiscale entropy optimization to take care of the fact that previous maximum state entropy, for lifelong exploration with millions of state observations, suffers from vanishing rewards and becomes very expensive computationally across iterations. Therefore, we add an episodic maximum entropy over each episode to speedup the search further. Second, we propose a novel intrinsic reward for episodic entropy maximization named \emph{average episodic state entropy} which provides the optimal solution for a theoretical upper bound of the episodic state entropy objective. Third, to speed the lifelong entropy maximization, we propose a $k$ nearest neighbors ($k$NN) graph to organize the estimation of the entropy and updating processes that reduces the computation substantially. Our ELEMENT significantly outperforms state-of-the-art intrinsic rewards in both episodic and lifelong setups. Moreover, it can be exploited in task-agnostic pre-training, collecting data for offline reinforcement learning, etc.

Discovering Common Information in Multi-view Data

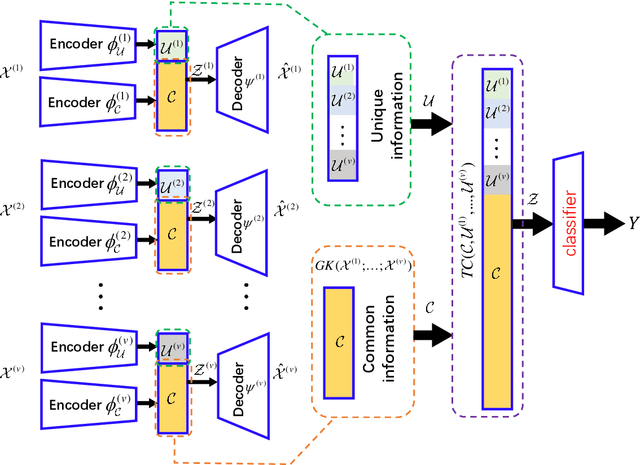
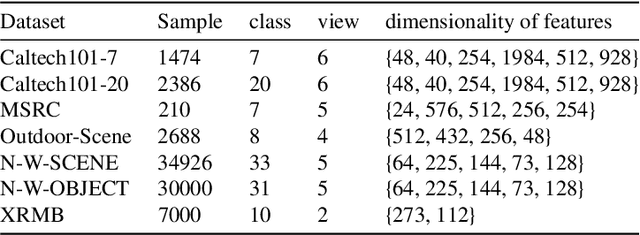
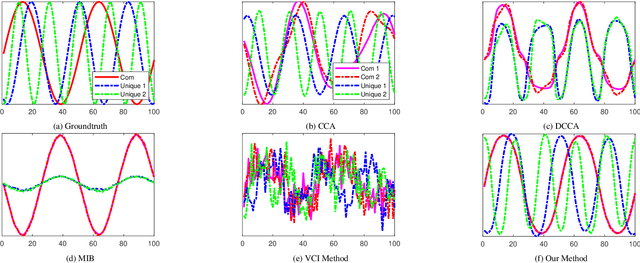
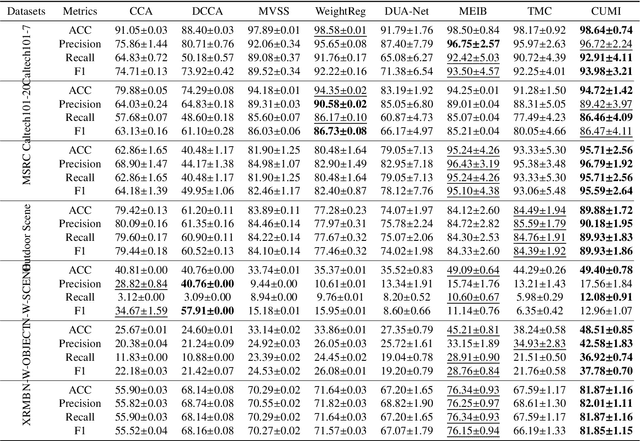
We introduce an innovative and mathematically rigorous definition for computing common information from multi-view data, drawing inspiration from G\'acs-K\"orner common information in information theory. Leveraging this definition, we develop a novel supervised multi-view learning framework to capture both common and unique information. By explicitly minimizing a total correlation term, the extracted common information and the unique information from each view are forced to be independent of each other, which, in turn, theoretically guarantees the effectiveness of our framework. To estimate information-theoretic quantities, our framework employs matrix-based R{\'e}nyi's $\alpha$-order entropy functional, which forgoes the need for variational approximation and distributional estimation in high-dimensional space. Theoretical proof is provided that our framework can faithfully discover both common and unique information from multi-view data. Experiments on synthetic and seven benchmark real-world datasets demonstrate the superior performance of our proposed framework over state-of-the-art approaches.

BAN: Detecting Backdoors Activated by Adversarial Neuron Noise

Backdoor attacks on deep learning represent a recent threat that has gained significant attention in the research community. Backdoor defenses are mainly based on backdoor inversion, which has been shown to be generic, model-agnostic, and applicable to practical threat scenarios. State-of-the-art backdoor inversion recovers a mask in the feature space to locate prominent backdoor features, where benign and backdoor features can be disentangled. However, it suffers from high computational overhead, and we also find that it overly relies on prominent backdoor features that are highly distinguishable from benign features. To tackle these shortcomings, this paper improves backdoor feature inversion for backdoor detection by incorporating extra neuron activation information. In particular, we adversarially increase the loss of backdoored models with respect to weights to activate the backdoor effect, based on which we can easily differentiate backdoored and clean models. Experimental results demonstrate our defense, BAN, is 1.37$\times$ (on CIFAR-10) and 5.11$\times$ (on ImageNet200) more efficient with 9.99% higher detect success rate than the state-of-the-art defense BTI-DBF. Our code and trained models are publicly available.\url{https://anonymous.4open.science/r/ban-4B32}

Domain Adaptation with Cauchy-Schwarz Divergence

Domain adaptation aims to use training data from one or multiple source domains to learn a hypothesis that can be generalized to a different, but related, target domain. As such, having a reliable measure for evaluating the discrepancy of both marginal and conditional distributions is crucial. We introduce Cauchy-Schwarz (CS) divergence to the problem of unsupervised domain adaptation (UDA). The CS divergence offers a theoretically tighter generalization error bound than the popular Kullback-Leibler divergence. This holds for the general case of supervised learning, including multi-class classification and regression. Furthermore, we illustrate that the CS divergence enables a simple estimator on the discrepancy of both marginal and conditional distributions between source and target domains in the representation space, without requiring any distributional assumptions. We provide multiple examples to illustrate how the CS divergence can be conveniently used in both distance metric- or adversarial training-based UDA frameworks, resulting in compelling performance.

Jacobian Regularizer-based Neural Granger Causality

With the advancement of neural networks, diverse methods for neural Granger causality have emerged, which demonstrate proficiency in handling complex data, and nonlinear relationships. However, the existing framework of neural Granger causality has several limitations. It requires the construction of separate predictive models for each target variable, and the relationship depends on the sparsity on the weights of the first layer, resulting in challenges in effectively modeling complex relationships between variables as well as unsatisfied estimation accuracy of Granger causality. Moreover, most of them cannot grasp full-time Granger causality. To address these drawbacks, we propose a Jacobian Regularizer-based Neural Granger Causality (JRNGC) approach, a straightforward yet highly effective method for learning multivariate summary Granger causality and full-time Granger causality by constructing a single model for all target variables. Specifically, our method eliminates the sparsity constraints of weights by leveraging an input-output Jacobian matrix regularizer, which can be subsequently represented as the weighted causal matrix in the post-hoc analysis. Extensive experiments show that our proposed approach achieves competitive performance with the state-of-the-art methods for learning summary Granger causality and full-time Granger causality while maintaining lower model complexity and high scalability.

Generalized Cauchy-Schwarz Divergence and Its Deep Learning Applications

Divergence measures play a central role in machine learning and become increasingly essential in deep learning. However, valid and computationally efficient divergence measures for multiple (more than two) distributions are scarcely investigated. This becomes particularly crucial in areas where the simultaneous management of multiple distributions is both unavoidable and essential. Examples include clustering, multi-source domain adaptation or generalization, and multi-view learning, among others. Although calculating the mean of pairwise distances between any two distributions serves as a common way to quantify the total divergence among multiple distributions, it is crucial to acknowledge that this approach is not straightforward and requires significant computational resources. In this study, we introduce a new divergence measure for multiple distributions named the generalized Cauchy-Schwarz divergence (GCSD), which is inspired by the classic Cauchy-Schwarz divergence. Additionally, we provide a closed-form sample estimator based on kernel density estimation, making it convenient and straightforward to use in various machine-learning applications. Finally, we apply the proposed GCSD to two challenging machine learning tasks, namely deep learning-based clustering and the problem of multi-source domain adaptation. The experimental results showcase the impressive performance of GCSD in both tasks, highlighting its potential application in machine-learning areas that involve quantifying multiple distributions.

Cauchy-Schwarz Divergence Information Bottleneck for Regression

The information bottleneck (IB) approach is popular to improve the generalization, robustness and explainability of deep neural networks. Essentially, it aims to find a minimum sufficient representation $\mathbf{t}$ by striking a trade-off between a compression term $I(\mathbf{x};\mathbf{t})$ and a prediction term $I(y;\mathbf{t})$, where $I(\cdot;\cdot)$ refers to the mutual information (MI). MI is for the IB for the most part expressed in terms of the Kullback-Leibler (KL) divergence, which in the regression case corresponds to prediction based on mean squared error (MSE) loss with Gaussian assumption and compression approximated by variational inference. In this paper, we study the IB principle for the regression problem and develop a new way to parameterize the IB with deep neural networks by exploiting favorable properties of the Cauchy-Schwarz (CS) divergence. By doing so, we move away from MSE-based regression and ease estimation by avoiding variational approximations or distributional assumptions. We investigate the improved generalization ability of our proposed CS-IB and demonstrate strong adversarial robustness guarantees. We demonstrate its superior performance on six real-world regression tasks over other popular deep IB approaches. We additionally observe that the solutions discovered by CS-IB always achieve the best trade-off between prediction accuracy and compression ratio in the information plane. The code is available at \url{https://github.com/SJYuCNEL/Cauchy-Schwarz-Information-Bottleneck}.

MIMIR: Masked Image Modeling for Mutual Information-based Adversarial Robustness

Vision Transformers (ViTs) achieve superior performance on various tasks compared to convolutional neural networks (CNNs), but ViTs are also vulnerable to adversarial attacks. Adversarial training is one of the most successful methods to build robust CNN models. Thus, recent works explored new methodologies for adversarial training of ViTs based on the differences between ViTs and CNNs, such as better training strategies, preventing attention from focusing on a single block, or discarding low-attention embeddings. However, these methods still follow the design of traditional supervised adversarial training, limiting the potential of adversarial training on ViTs. This paper proposes a novel defense method, MIMIR, which aims to build a different adversarial training methodology by utilizing Masked Image Modeling at pre-training. We create an autoencoder that accepts adversarial examples as input but takes the clean examples as the modeling target. Then, we create a mutual information (MI) penalty following the idea of the Information Bottleneck. Among the two information source inputs and corresponding adversarial perturbation, the perturbation information is eliminated due to the constraint of the modeling target. Next, we provide a theoretical analysis of MIMIR using the bounds of the MI penalty. We also design two adaptive attacks when the adversary is aware of the MIMIR defense and show that MIMIR still performs well. The experimental results show that MIMIR improves (natural and adversarial) accuracy on average by 4.19\% on CIFAR-10 and 5.52\% on ImageNet-1K, compared to baselines. On Tiny-ImageNet, we obtained improved natural accuracy of 2.99\% on average and comparable adversarial accuracy. Our code and trained models are publicly available\footnote{\url{https://anonymous.4open.science/r/MIMIR-5444/README.md}}.

Continual Invariant Risk Minimization

Empirical risk minimization can lead to poor generalization behavior on unseen environments if the learned model does not capture invariant feature representations. Invariant risk minimization (IRM) is a recent proposal for discovering environment-invariant representations. IRM was introduced by Arjovsky et al. (2019) and extended by Ahuja et al. (2020). IRM assumes that all environments are available to the learning system at the same time. With this work, we generalize the concept of IRM to scenarios where environments are observed sequentially. We show that existing approaches, including those designed for continual learning, fail to identify the invariant features and models across sequentially presented environments. We extend IRM under a variational Bayesian and bilevel framework, creating a general approach to continual invariant risk minimization. We also describe a strategy to solve the optimization problems using a variant of the alternating direction method of multiplier (ADMM). We show empirically using multiple datasets and with multiple sequential environments that the proposed methods outperform or is competitive with prior approaches.

Revisiting the Robustness of the Minimum Error Entropy Criterion: A Transfer Learning Case Study

Coping with distributional shifts is an important part of transfer learning methods in order to perform well in real-life tasks. However, most of the existing approaches in this area either focus on an ideal scenario in which the data does not contain noises or employ a complicated training paradigm or model design to deal with distributional shifts. In this paper, we revisit the robustness of the minimum error entropy (MEE) criterion, a widely used objective in statistical signal processing to deal with non-Gaussian noises, and investigate its feasibility and usefulness in real-life transfer learning regression tasks, where distributional shifts are common. Specifically, we put forward a new theoretical result showing the robustness of MEE against covariate shift. We also show that by simply replacing the mean squared error (MSE) loss with the MEE on basic transfer learning algorithms such as fine-tuning and linear probing, we can achieve competitive performance with respect to state-of-the-art transfer learning algorithms. We justify our arguments on both synthetic data and 5 real-world time-series data.