Yuxin Dong
Kimi K2.5: Visual Agentic Intelligence
Feb 02, 2026Abstract:We introduce Kimi K2.5, an open-source multimodal agentic model designed to advance general agentic intelligence. K2.5 emphasizes the joint optimization of text and vision so that two modalities enhance each other. This includes a series of techniques such as joint text-vision pre-training, zero-vision SFT, and joint text-vision reinforcement learning. Building on this multimodal foundation, K2.5 introduces Agent Swarm, a self-directed parallel agent orchestration framework that dynamically decomposes complex tasks into heterogeneous sub-problems and executes them concurrently. Extensive evaluations show that Kimi K2.5 achieves state-of-the-art results across various domains including coding, vision, reasoning, and agentic tasks. Agent Swarm also reduces latency by up to $4.5\times$ over single-agent baselines. We release the post-trained Kimi K2.5 model checkpoint to facilitate future research and real-world applications of agentic intelligence.
Understanding Task Vectors in In-Context Learning: Emergence, Functionality, and Limitations
Jun 10, 2025Abstract:Task vectors offer a compelling mechanism for accelerating inference in in-context learning (ICL) by distilling task-specific information into a single, reusable representation. Despite their empirical success, the underlying principles governing their emergence and functionality remain unclear. This work proposes the Linear Combination Conjecture, positing that task vectors act as single in-context demonstrations formed through linear combinations of the original ones. We provide both theoretical and empirical support for this conjecture. First, we show that task vectors naturally emerge in linear transformers trained on triplet-formatted prompts through loss landscape analysis. Next, we predict the failure of task vectors on representing high-rank mappings and confirm this on practical LLMs. Our findings are further validated through saliency analyses and parameter visualization, suggesting an enhancement of task vectors by injecting multiple ones into few-shot prompts. Together, our results advance the understanding of task vectors and shed light on the mechanisms underlying ICL in transformer-based models.
From Compression to Expansion: A Layerwise Analysis of In-Context Learning
May 22, 2025Abstract:In-context learning (ICL) enables large language models (LLMs) to adapt to new tasks without weight updates by learning from demonstration sequences. While ICL shows strong empirical performance, its internal representational mechanisms are not yet well understood. In this work, we conduct a statistical geometric analysis of ICL representations to investigate how task-specific information is captured across layers. Our analysis reveals an intriguing phenomenon, which we term *Layerwise Compression-Expansion*: early layers progressively produce compact and discriminative representations that encode task information from the input demonstrations, while later layers expand these representations to incorporate the query and generate the prediction. This phenomenon is observed consistently across diverse tasks and a range of contemporary LLM architectures. We demonstrate that it has important implications for ICL performance -- improving with model size and the number of demonstrations -- and for robustness in the presence of noisy examples. To further understand the effect of the compact task representation, we propose a bias-variance decomposition and provide a theoretical analysis showing how attention mechanisms contribute to reducing both variance and bias, thereby enhancing performance as the number of demonstrations increases. Our findings reveal an intriguing layerwise dynamic in ICL, highlight how structured representations emerge within LLMs, and showcase that analyzing internal representations can facilitate a deeper understanding of model behavior.
Towards the Generalization of Multi-view Learning: An Information-theoretical Analysis
Jan 28, 2025Abstract:Multiview learning has drawn widespread attention for its efficacy in leveraging cross-view consensus and complementarity information to achieve a comprehensive representation of data. While multi-view learning has undergone vigorous development and achieved remarkable success, the theoretical understanding of its generalization behavior remains elusive. This paper aims to bridge this gap by developing information-theoretic generalization bounds for multi-view learning, with a particular focus on multi-view reconstruction and classification tasks. Our bounds underscore the importance of capturing both consensus and complementary information from multiple different views to achieve maximally disentangled representations. These results also indicate that applying the multi-view information bottleneck regularizer is beneficial for satisfactory generalization performance. Additionally, we derive novel data-dependent bounds under both leave-one-out and supersample settings, yielding computational tractable and tighter bounds. In the interpolating regime, we further establish the fast-rate bound for multi-view learning, exhibiting a faster convergence rate compared to conventional square-root bounds. Numerical results indicate a strong correlation between the true generalization gap and the derived bounds across various learning scenarios.
Towards Sharper Information-theoretic Generalization Bounds for Meta-Learning
Jan 26, 2025
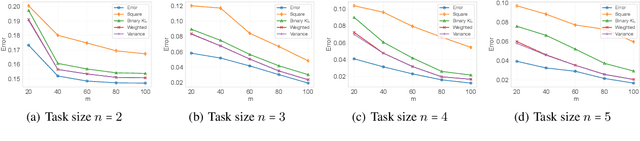

Abstract:In recent years, information-theoretic generalization bounds have emerged as a promising approach for analyzing the generalization capabilities of meta-learning algorithms. However, existing results are confined to two-step bounds, failing to provide a sharper characterization of the meta-generalization gap that simultaneously accounts for environment-level and task-level dependencies. This paper addresses this fundamental limitation by establishing novel single-step information-theoretic bounds for meta-learning. Our bounds exhibit substantial advantages over prior MI- and CMI-based bounds, especially in terms of tightness, scaling behavior associated with sampled tasks and samples per task, and computational tractability. Furthermore, we provide novel theoretical insights into the generalization behavior of two classes of noise and iterative meta-learning algorithms via gradient covariance analysis, where the meta-learner uses either the entire meta-training data (e.g., Reptile), or separate training and test data within the task (e.g., model agnostic meta-learning (MAML)). Numerical results validate the effectiveness of the derived bounds in capturing the generalization dynamics of meta-learning.
Stock Type Prediction Model Based on Hierarchical Graph Neural Network
Dec 09, 2024

Abstract:This paper introduces a novel approach to stock data analysis by employing a Hierarchical Graph Neural Network (HGNN) model that captures multi-level information and relational structures in the stock market. The HGNN model integrates stock relationship data and hierarchical attributes to predict stock types effectively. The paper discusses the construction of a stock industry relationship graph and the extraction of temporal information from historical price sequences. It also highlights the design of a graph convolution operation and a temporal attention aggregator to model the macro market state. The integration of these features results in a comprehensive stock prediction model that addresses the challenges of utilizing stock relationship data and modeling hierarchical attributes in the stock market.
Advanced RAG Models with Graph Structures: Optimizing Complex Knowledge Reasoning and Text Generation
Nov 06, 2024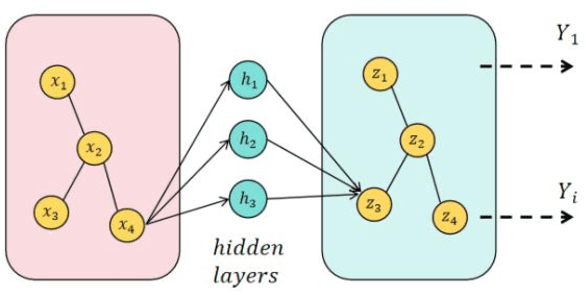
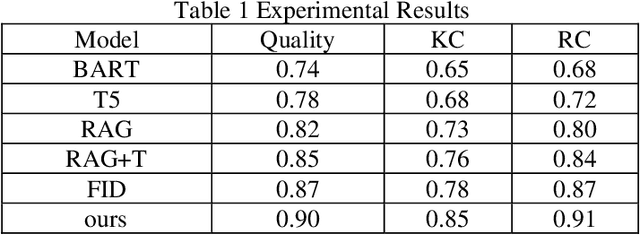
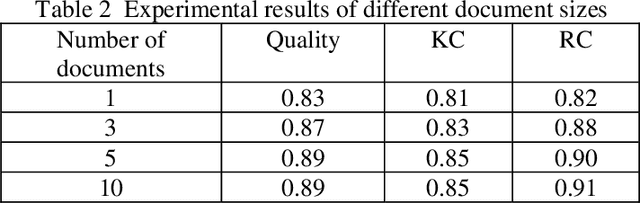
Abstract:This study aims to optimize the existing retrieval-augmented generation model (RAG) by introducing a graph structure to improve the performance of the model in dealing with complex knowledge reasoning tasks. The traditional RAG model has the problem of insufficient processing efficiency when facing complex graph structure information (such as knowledge graphs, hierarchical relationships, etc.), which affects the quality and consistency of the generated results. This study proposes a scheme to process graph structure data by combining graph neural network (GNN), so that the model can capture the complex relationship between entities, thereby improving the knowledge consistency and reasoning ability of the generated text. The experiment used the Natural Questions (NQ) dataset and compared it with multiple existing generation models. The results show that the graph-based RAG model proposed in this paper is superior to the traditional generation model in terms of quality, knowledge consistency, and reasoning ability, especially when dealing with tasks that require multi-dimensional reasoning. Through the combination of the enhancement of the retrieval module and the graph neural network, the model in this study can better handle complex knowledge background information and has broad potential value in multiple practical application scenarios.
Automated Genre-Aware Article Scoring and Feedback Using Large Language Models
Oct 18, 2024



Abstract:This paper focuses on the development of an advanced intelligent article scoring system that not only assesses the overall quality of written work but also offers detailed feature-based scoring tailored to various article genres. By integrating the pre-trained BERT model with the large language model Chat-GPT, the system gains a deep understanding of both the content and structure of the text, enabling it to provide a thorough evaluation along with targeted suggestions for improvement. Experimental results demonstrate that this system outperforms traditional scoring methods across multiple public datasets, particularly in feature-based assessments, offering a more accurate reflection of the quality of different article types. Moreover, the system generates personalized feedback to assist users in enhancing their writing skills, underscoring the potential and practical value of automated scoring technologies in educational contexts.
Dynamic Fraud Detection: Integrating Reinforcement Learning into Graph Neural Networks
Sep 15, 2024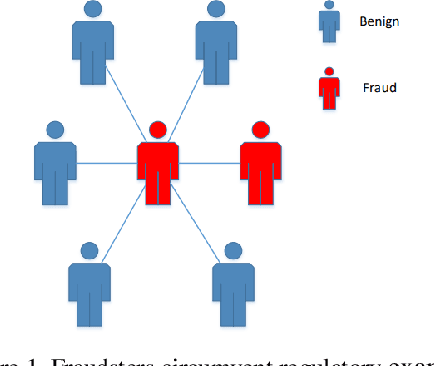
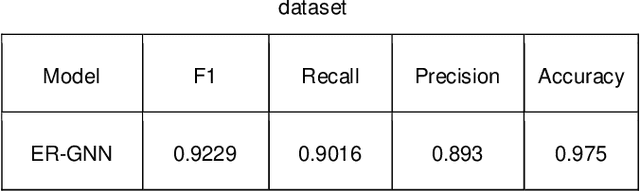
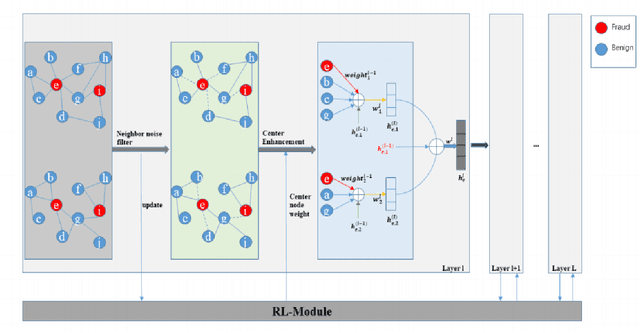
Abstract:Financial fraud refers to the act of obtaining financial benefits through dishonest means. Such behavior not only disrupts the order of the financial market but also harms economic and social development and breeds other illegal and criminal activities. With the popularization of the internet and online payment methods, many fraudulent activities and money laundering behaviors in life have shifted from offline to online, posing a great challenge to regulatory authorities. How to efficiently detect these financial fraud activities has become an urgent issue that needs to be resolved. Graph neural networks are a type of deep learning model that can utilize the interactive relationships within graph structures, and they have been widely applied in the field of fraud detection. However, there are still some issues. First, fraudulent activities only account for a very small part of transaction transfers, leading to an inevitable problem of label imbalance in fraud detection. At the same time, fraudsters often disguise their behavior, which can have a negative impact on the final prediction results. In addition, existing research has overlooked the importance of balancing neighbor information and central node information. For example, when the central node has too many neighbors, the features of the central node itself are often neglected. Finally, fraud activities and patterns are constantly changing over time, so considering the dynamic evolution of graph edge relationships is also very important.
How Does Distribution Matching Help Domain Generalization: An Information-theoretic Analysis
Jun 14, 2024Abstract:Domain generalization aims to learn invariance across multiple training domains, thereby enhancing generalization against out-of-distribution data. While gradient or representation matching algorithms have achieved remarkable success, these methods generally lack generalization guarantees or depend on strong assumptions, leaving a gap in understanding the underlying mechanism of distribution matching. In this work, we formulate domain generalization from a novel probabilistic perspective, ensuring robustness while avoiding overly conservative solutions. Through comprehensive information-theoretic analysis, we provide key insights into the roles of gradient and representation matching in promoting generalization. Our results reveal the complementary relationship between these two components, indicating that existing works focusing solely on either gradient or representation alignment are insufficient to solve the domain generalization problem. In light of these theoretical findings, we introduce IDM to simultaneously align the inter-domain gradients and representations. Integrated with the proposed PDM method for complex distribution matching, IDM achieves superior performance over various baseline methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge