ViLa-MIL: Dual-scale Vision-Language Multiple Instance Learning for Whole Slide Image Classification

Multiple instance learning (MIL)-based framework has become the mainstream for processing the whole slide image (WSI) with giga-pixel size and hierarchical image context in digital pathology. However, these methods heavily depend on a substantial number of bag-level labels and solely learn from the original slides, which are easily affected by variations in data distribution. Recently, vision language model (VLM)-based methods introduced the language prior by pre-training on large-scale pathological image-text pairs. However, the previous text prompt lacks the consideration of pathological prior knowledge, therefore does not substantially boost the model's performance. Moreover, the collection of such pairs and the pre-training process are very time-consuming and source-intensive.To solve the above problems, we propose a dual-scale vision-language multiple instance learning (ViLa-MIL) framework for whole slide image classification. Specifically, we propose a dual-scale visual descriptive text prompt based on the frozen large language model (LLM) to boost the performance of VLM effectively. To transfer the VLM to process WSI efficiently, for the image branch, we propose a prototype-guided patch decoder to aggregate the patch features progressively by grouping similar patches into the same prototype; for the text branch, we introduce a context-guided text decoder to enhance the text features by incorporating the multi-granular image contexts. Extensive studies on three multi-cancer and multi-center subtyping datasets demonstrate the superiority of ViLa-MIL.

Towards the Generalization of Multi-view Learning: An Information-theoretical Analysis

Multiview learning has drawn widespread attention for its efficacy in leveraging cross-view consensus and complementarity information to achieve a comprehensive representation of data. While multi-view learning has undergone vigorous development and achieved remarkable success, the theoretical understanding of its generalization behavior remains elusive. This paper aims to bridge this gap by developing information-theoretic generalization bounds for multi-view learning, with a particular focus on multi-view reconstruction and classification tasks. Our bounds underscore the importance of capturing both consensus and complementary information from multiple different views to achieve maximally disentangled representations. These results also indicate that applying the multi-view information bottleneck regularizer is beneficial for satisfactory generalization performance. Additionally, we derive novel data-dependent bounds under both leave-one-out and supersample settings, yielding computational tractable and tighter bounds. In the interpolating regime, we further establish the fast-rate bound for multi-view learning, exhibiting a faster convergence rate compared to conventional square-root bounds. Numerical results indicate a strong correlation between the true generalization gap and the derived bounds across various learning scenarios.

Towards Sharper Information-theoretic Generalization Bounds for Meta-Learning

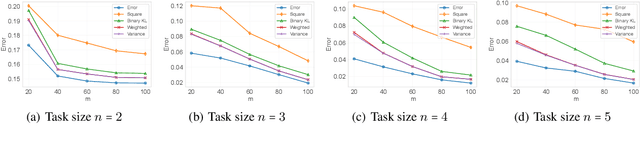
In recent years, information-theoretic generalization bounds have emerged as a promising approach for analyzing the generalization capabilities of meta-learning algorithms. However, existing results are confined to two-step bounds, failing to provide a sharper characterization of the meta-generalization gap that simultaneously accounts for environment-level and task-level dependencies. This paper addresses this fundamental limitation by establishing novel single-step information-theoretic bounds for meta-learning. Our bounds exhibit substantial advantages over prior MI- and CMI-based bounds, especially in terms of tightness, scaling behavior associated with sampled tasks and samples per task, and computational tractability. Furthermore, we provide novel theoretical insights into the generalization behavior of two classes of noise and iterative meta-learning algorithms via gradient covariance analysis, where the meta-learner uses either the entire meta-training data (e.g., Reptile), or separate training and test data within the task (e.g., model agnostic meta-learning (MAML)). Numerical results validate the effectiveness of the derived bounds in capturing the generalization dynamics of meta-learning.

Rectified Diffusion Guidance for Conditional Generation

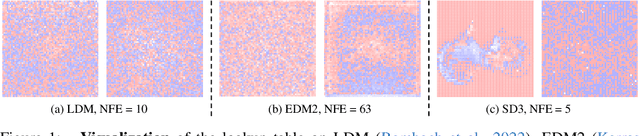
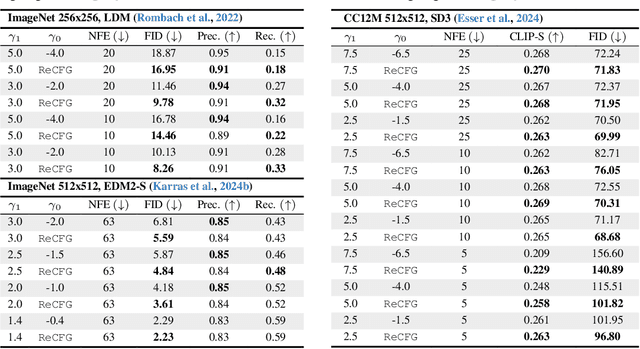
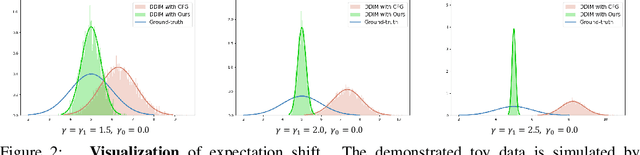
Classifier-Free Guidance (CFG), which combines the conditional and unconditional score functions with two coefficients summing to one, serves as a practical technique for diffusion model sampling. Theoretically, however, denoising with CFG cannot be expressed as a reciprocal diffusion process, which may consequently leave some hidden risks during use. In this work, we revisit the theory behind CFG and rigorously confirm that the improper configuration of the combination coefficients (i.e., the widely used summing-to-one version) brings about expectation shift of the generative distribution. To rectify this issue, we propose ReCFG with a relaxation on the guidance coefficients such that denoising with ReCFG strictly aligns with the diffusion theory. We further show that our approach enjoys a closed-form solution given the guidance strength. That way, the rectified coefficients can be readily pre-computed via traversing the observed data, leaving the sampling speed barely affected. Empirical evidence on real-world data demonstrate the compatibility of our post-hoc design with existing state-of-the-art diffusion models, including both class-conditioned ones (e.g., EDM2 on ImageNet) and text-conditioned ones (e.g., SD3 on CC12M), without any retraining. We will open-source the code to facilitate further research.

Accelerating Non-Maximum Suppression: A Graph Theory Perspective

Non-maximum suppression (NMS) is an indispensable post-processing step in object detection. With the continuous optimization of network models, NMS has become the ``last mile'' to enhance the efficiency of object detection. This paper systematically analyzes NMS from a graph theory perspective for the first time, revealing its intrinsic structure. Consequently, we propose two optimization methods, namely QSI-NMS and BOE-NMS. The former is a fast recursive divide-and-conquer algorithm with negligible mAP loss, and its extended version (eQSI-NMS) achieves optimal complexity of $\mathcal{O}(n\log n)$. The latter, concentrating on the locality of NMS, achieves an optimization at a constant level without an mAP loss penalty. Moreover, to facilitate rapid evaluation of NMS methods for researchers, we introduce NMS-Bench, the first benchmark designed to comprehensively assess various NMS methods. Taking the YOLOv8-N model on MS COCO 2017 as the benchmark setup, our method QSI-NMS provides $6.2\times$ speed of original NMS on the benchmark, with a $0.1\%$ decrease in mAP. The optimal eQSI-NMS, with only a $0.3\%$ mAP decrease, achieves $10.7\times$ speed. Meanwhile, BOE-NMS exhibits $5.1\times$ speed with no compromise in mAP.

SpotActor: Training-Free Layout-Controlled Consistent Image Generation

Text-to-image diffusion models significantly enhance the efficiency of artistic creation with high-fidelity image generation. However, in typical application scenarios like comic book production, they can neither place each subject into its expected spot nor maintain the consistent appearance of each subject across images. For these issues, we pioneer a novel task, Layout-to-Consistent-Image (L2CI) generation, which produces consistent and compositional images in accordance with the given layout conditions and text prompts. To accomplish this challenging task, we present a new formalization of dual energy guidance with optimization in a dual semantic-latent space and thus propose a training-free pipeline, SpotActor, which features a layout-conditioned backward update stage and a consistent forward sampling stage. In the backward stage, we innovate a nuanced layout energy function to mimic the attention activations with a sigmoid-like objective. While in the forward stage, we design Regional Interconnection Self-Attention (RISA) and Semantic Fusion Cross-Attention (SFCA) mechanisms that allow mutual interactions across images. To evaluate the performance, we present ActorBench, a specified benchmark with hundreds of reasonable prompt-box pairs stemming from object detection datasets. Comprehensive experiments are conducted to demonstrate the effectiveness of our method. The results prove that SpotActor fulfills the expectations of this task and showcases the potential for practical applications with superior layout alignment, subject consistency, prompt conformity and background diversity.

How Does Distribution Matching Help Domain Generalization: An Information-theoretic Analysis

Domain generalization aims to learn invariance across multiple training domains, thereby enhancing generalization against out-of-distribution data. While gradient or representation matching algorithms have achieved remarkable success, these methods generally lack generalization guarantees or depend on strong assumptions, leaving a gap in understanding the underlying mechanism of distribution matching. In this work, we formulate domain generalization from a novel probabilistic perspective, ensuring robustness while avoiding overly conservative solutions. Through comprehensive information-theoretic analysis, we provide key insights into the roles of gradient and representation matching in promoting generalization. Our results reveal the complementary relationship between these two components, indicating that existing works focusing solely on either gradient or representation alignment are insufficient to solve the domain generalization problem. In light of these theoretical findings, we introduce IDM to simultaneously align the inter-domain gradients and representations. Integrated with the proposed PDM method for complex distribution matching, IDM achieves superior performance over various baseline methods.

Understanding the Generalization Ability of Deep Learning Algorithms: A Kernelized Renyi's Entropy Perspective

Recently, information theoretic analysis has become a popular framework for understanding the generalization behavior of deep neural networks. It allows a direct analysis for stochastic gradient/Langevin descent (SGD/SGLD) learning algorithms without strong assumptions such as Lipschitz or convexity conditions. However, the current generalization error bounds within this framework are still far from optimal, while substantial improvements on these bounds are quite challenging due to the intractability of high-dimensional information quantities. To address this issue, we first propose a novel information theoretical measure: kernelized Renyi's entropy, by utilizing operator representation in Hilbert space. It inherits the properties of Shannon's entropy and can be effectively calculated via simple random sampling, while remaining independent of the input dimension. We then establish the generalization error bounds for SGD/SGLD under kernelized Renyi's entropy, where the mutual information quantities can be directly calculated, enabling evaluation of the tightness of each intermediate step. We show that our information-theoretical bounds depend on the statistics of the stochastic gradients evaluated along with the iterates, and are rigorously tighter than the current state-of-the-art (SOTA) results. The theoretical findings are also supported by large-scale empirical studies1.

On the Stability and Generalization of Triplet Learning

Triplet learning, i.e. learning from triplet data, has attracted much attention in computer vision tasks with an extremely large number of categories, e.g., face recognition and person re-identification. Albeit with rapid progress in designing and applying triplet learning algorithms, there is a lacking study on the theoretical understanding of their generalization performance. To fill this gap, this paper investigates the generalization guarantees of triplet learning by leveraging the stability analysis. Specifically, we establish the first general high-probability generalization bound for the triplet learning algorithm satisfying the uniform stability, and then obtain the excess risk bounds of the order $O(n^{-\frac{1}{2}} \mathrm{log}n)$ for both stochastic gradient descent (SGD) and regularized risk minimization (RRM), where $2n$ is approximately equal to the number of training samples. Moreover, an optimistic generalization bound in expectation as fast as $O(n^{-1})$ is derived for RRM in a low noise case via the on-average stability analysis. Finally, our results are applied to triplet metric learning to characterize its theoretical underpinning.

Robust and Fast Measure of Information via Low-rank Representation

The matrix-based R\'enyi's entropy allows us to directly quantify information measures from given data, without explicit estimation of the underlying probability distribution. This intriguing property makes it widely applied in statistical inference and machine learning tasks. However, this information theoretical quantity is not robust against noise in the data, and is computationally prohibitive in large-scale applications. To address these issues, we propose a novel measure of information, termed low-rank matrix-based R\'enyi's entropy, based on low-rank representations of infinitely divisible kernel matrices. The proposed entropy functional inherits the specialty of of the original definition to directly quantify information from data, but enjoys additional advantages including robustness and effective calculation. Specifically, our low-rank variant is more sensitive to informative perturbations induced by changes in underlying distributions, while being insensitive to uninformative ones caused by noises. Moreover, low-rank R\'enyi's entropy can be efficiently approximated by random projection and Lanczos iteration techniques, reducing the overall complexity from $\mathcal{O}(n^3)$ to $\mathcal{O}(n^2 s)$ or even $\mathcal{O}(ns^2)$, where $n$ is the number of data samples and $s \ll n$. We conduct large-scale experiments to evaluate the effectiveness of this new information measure, demonstrating superior results compared to matrix-based R\'enyi's entropy in terms of both performance and computational efficiency.