Stability-based Generalization Analysis for Mixtures of Pointwise and Pairwise Learning

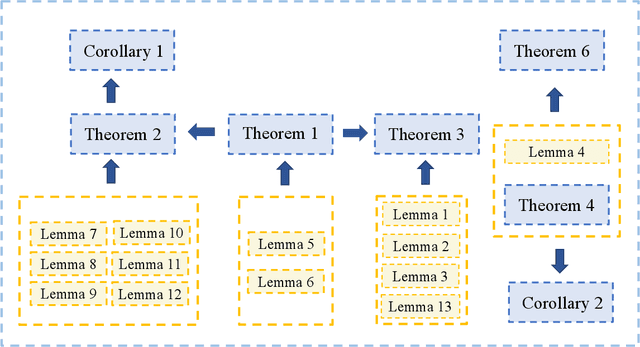
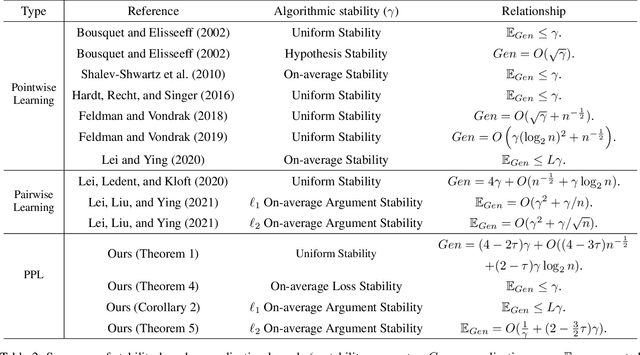
Recently, some mixture algorithms of pointwise and pairwise learning (PPL) have been formulated by employing the hybrid error metric of "pointwise loss + pairwise loss" and have shown empirical effectiveness on feature selection, ranking and recommendation tasks. However, to the best of our knowledge, the learning theory foundation of PPL has not been touched in the existing works. In this paper, we try to fill this theoretical gap by investigating the generalization properties of PPL. After extending the definitions of algorithmic stability to the PPL setting, we establish the high-probability generalization bounds for uniformly stable PPL algorithms. Moreover, explicit convergence rates of stochastic gradient descent (SGD) and regularized risk minimization (RRM) for PPL are stated by developing the stability analysis technique of pairwise learning. In addition, the refined generalization bounds of PPL are obtained by replacing uniform stability with on-average stability.

On the Stability and Generalization of Triplet Learning

Triplet learning, i.e. learning from triplet data, has attracted much attention in computer vision tasks with an extremely large number of categories, e.g., face recognition and person re-identification. Albeit with rapid progress in designing and applying triplet learning algorithms, there is a lacking study on the theoretical understanding of their generalization performance. To fill this gap, this paper investigates the generalization guarantees of triplet learning by leveraging the stability analysis. Specifically, we establish the first general high-probability generalization bound for the triplet learning algorithm satisfying the uniform stability, and then obtain the excess risk bounds of the order $O(n^{-\frac{1}{2}} \mathrm{log}n)$ for both stochastic gradient descent (SGD) and regularized risk minimization (RRM), where $2n$ is approximately equal to the number of training samples. Moreover, an optimistic generalization bound in expectation as fast as $O(n^{-1})$ is derived for RRM in a low noise case via the on-average stability analysis. Finally, our results are applied to triplet metric learning to characterize its theoretical underpinning.

Error-based Knockoffs Inference for Controlled Feature Selection

Recently, the scheme of model-X knockoffs was proposed as a promising solution to address controlled feature selection under high-dimensional finite-sample settings. However, the procedure of model-X knockoffs depends heavily on the coefficient-based feature importance and only concerns the control of false discovery rate (FDR). To further improve its adaptivity and flexibility, in this paper, we propose an error-based knockoff inference method by integrating the knockoff features, the error-based feature importance statistics, and the stepdown procedure together. The proposed inference procedure does not require specifying a regression model and can handle feature selection with theoretical guarantees on controlling false discovery proportion (FDP), FDR, or k-familywise error rate (k-FWER). Empirical evaluations demonstrate the competitive performance of our approach on both simulated and real data.

Principal Model Analysis Based on Partial Least Squares

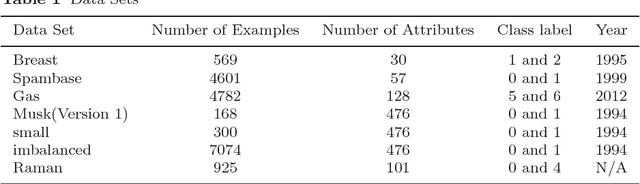
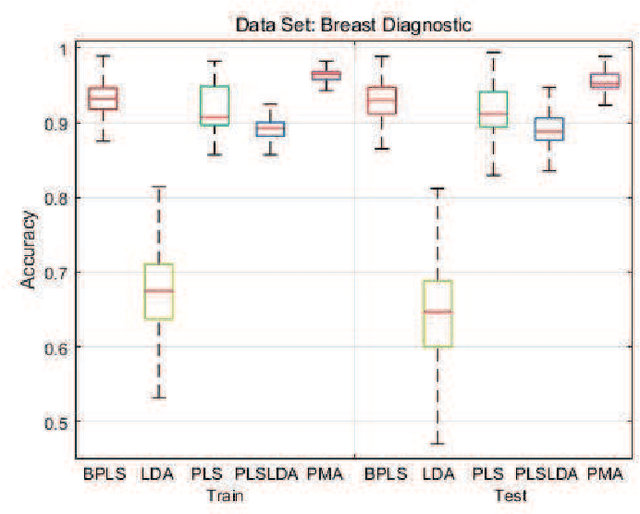
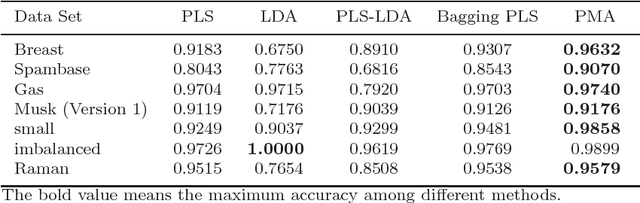
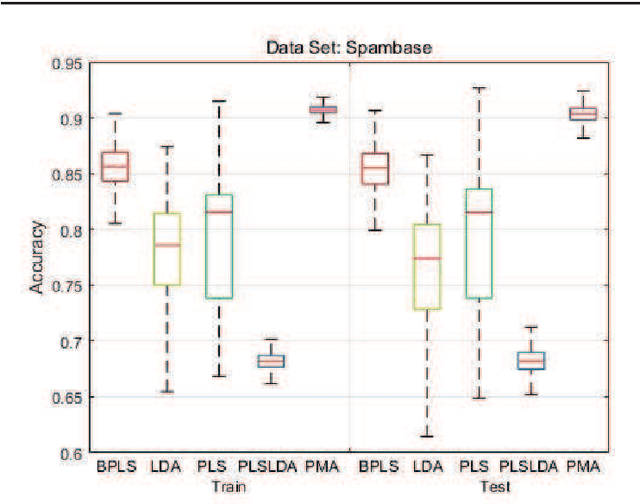
Motivated by the Bagging Partial Least Squares (PLS) and Principal Component Analysis (PCA) algorithms, we propose a Principal Model Analysis (PMA) method in this paper. In the proposed PMA algorithm, the PCA and the PLS are combined. In the method, multiple PLS models are trained on sub-training sets, derived from the original training set based on the random sampling with replacement method. The regression coefficients of all the sub-PLS models are fused in a joint regression coefficient matrix. The final projection direction is then estimated by performing the PCA on the joint regression coefficient matrix. The proposed PMA method is compared with other traditional dimension reduction methods, such as PLS, Bagging PLS, Linear discriminant analysis (LDA) and PLS-LDA. Experimental results on six public datasets show that our proposed method can achieve better classification performance and is usually more stable.