Low-PAPR OFDM-ISAC Waveform Design Based on Frequency-Domain Phase Differences

Low peak-to-average power ratio (PAPR) orthogonal frequency division multiplexing (OFDM) waveform design is a crucial issue in integrated sensing and communications (ISAC). This paper introduces an OFDM-ISAC waveform design that utilizes the entire spectrum simultaneously for both communication and sensing by leveraging a novel degree of freedom (DoF): the frequency-domain phase difference (PD). Based on this concept, we develop a novel PD-based OFDM-ISAC waveform structure and utilize it to design a PD-based Low-PAPR OFDM-ISAC (PLPOI) waveform. The design is formulated as an optimization problem incorporating four key constraints: the time-frequency relationship equation, frequency-domain unimodular constraints, PD constraints, and time-domain low PAPR requirements. To solve this challenging non-convex problem, we develop an efficient algorithm, ADMM-PLPOI, based on the alternating direction method of multipliers (ADMM) framework. Extensive simulation results demonstrate that the proposed PLPOI waveform achieves significant improvements in both PAPR and bit error rate (BER) performance compared to conventional OFDM-ISAC waveforms.

Breaking Memory Limits: Gradient Wavelet Transform Enhances LLMs Training

Large language models (LLMs) have shown impressive performance across a range of natural language processing tasks. However, their vast number of parameters introduces significant memory challenges during training, particularly when using memory-intensive optimizers like Adam. Existing memory-efficient algorithms often rely on techniques such as singular value decomposition projection or weight freezing. While these approaches help alleviate memory constraints, they generally produce suboptimal results compared to full-rank updates. In this paper, we investigate the memory-efficient method beyond low-rank training, proposing a novel solution called Gradient Wavelet Transform (GWT), which applies wavelet transforms to gradients in order to significantly reduce the memory requirements for maintaining optimizer states. We demonstrate that GWT can be seamlessly integrated with memory-intensive optimizers, enabling efficient training without sacrificing performance. Through extensive experiments on both pre-training and fine-tuning tasks, we show that GWT achieves state-of-the-art performance compared with advanced memory-efficient optimizers and full-rank approaches in terms of both memory usage and training performance.

Stability-based Generalization Analysis for Mixtures of Pointwise and Pairwise Learning

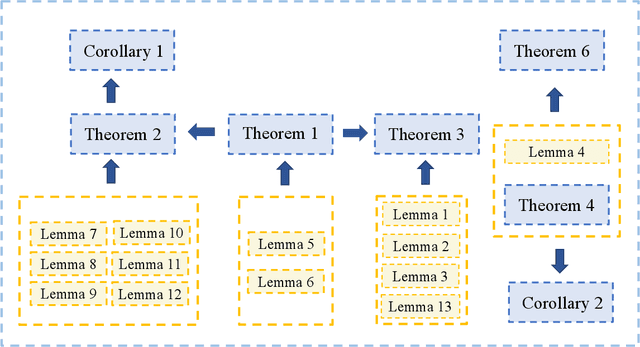
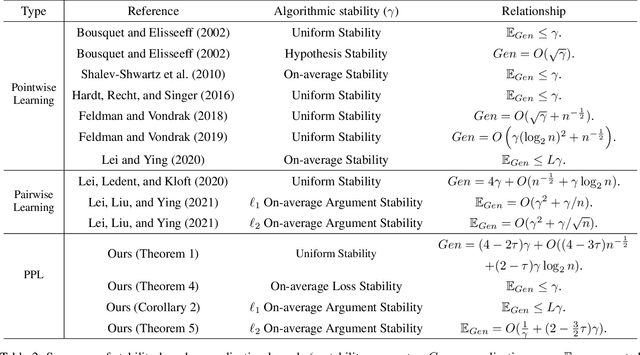
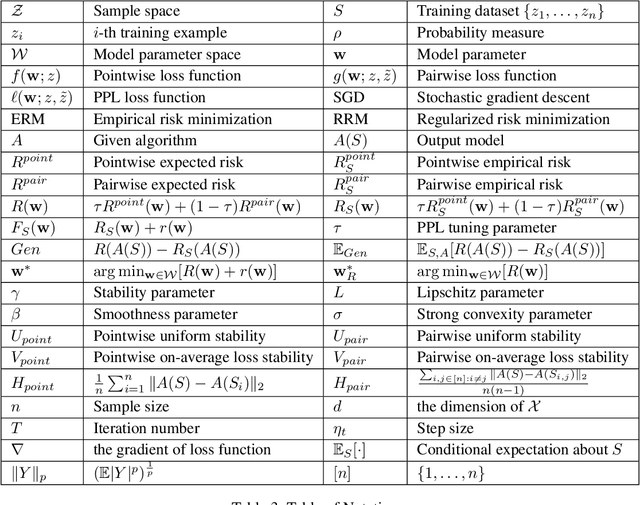
Recently, some mixture algorithms of pointwise and pairwise learning (PPL) have been formulated by employing the hybrid error metric of "pointwise loss + pairwise loss" and have shown empirical effectiveness on feature selection, ranking and recommendation tasks. However, to the best of our knowledge, the learning theory foundation of PPL has not been touched in the existing works. In this paper, we try to fill this theoretical gap by investigating the generalization properties of PPL. After extending the definitions of algorithmic stability to the PPL setting, we establish the high-probability generalization bounds for uniformly stable PPL algorithms. Moreover, explicit convergence rates of stochastic gradient descent (SGD) and regularized risk minimization (RRM) for PPL are stated by developing the stability analysis technique of pairwise learning. In addition, the refined generalization bounds of PPL are obtained by replacing uniform stability with on-average stability.