Breaking Memory Limits: Gradient Wavelet Transform Enhances LLMs Training

Large language models (LLMs) have shown impressive performance across a range of natural language processing tasks. However, their vast number of parameters introduces significant memory challenges during training, particularly when using memory-intensive optimizers like Adam. Existing memory-efficient algorithms often rely on techniques such as singular value decomposition projection or weight freezing. While these approaches help alleviate memory constraints, they generally produce suboptimal results compared to full-rank updates. In this paper, we investigate the memory-efficient method beyond low-rank training, proposing a novel solution called Gradient Wavelet Transform (GWT), which applies wavelet transforms to gradients in order to significantly reduce the memory requirements for maintaining optimizer states. We demonstrate that GWT can be seamlessly integrated with memory-intensive optimizers, enabling efficient training without sacrificing performance. Through extensive experiments on both pre-training and fine-tuning tasks, we show that GWT achieves state-of-the-art performance compared with advanced memory-efficient optimizers and full-rank approaches in terms of both memory usage and training performance.

Sharpness-Aware Minimization with Adaptive Regularization for Training Deep Neural Networks

Sharpness-Aware Minimization (SAM) has proven highly effective in improving model generalization in machine learning tasks. However, SAM employs a fixed hyperparameter associated with the regularization to characterize the sharpness of the model. Despite its success, research on adaptive regularization methods based on SAM remains scarce. In this paper, we propose the SAM with Adaptive Regularization (SAMAR), which introduces a flexible sharpness ratio rule to update the regularization parameter dynamically. We provide theoretical proof of the convergence of SAMAR for functions satisfying the Lipschitz continuity. Additionally, experiments on image recognition tasks using CIFAR-10 and CIFAR-100 demonstrate that SAMAR enhances accuracy and model generalization.

Federated Prediction-Powered Inference from Decentralized Data

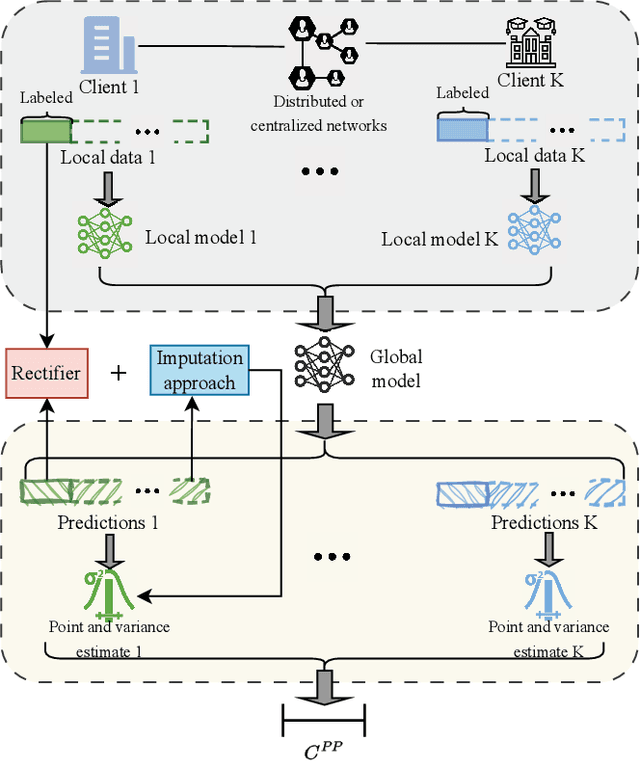
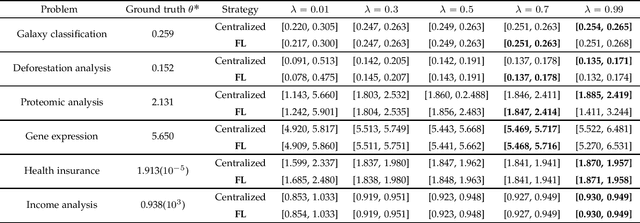
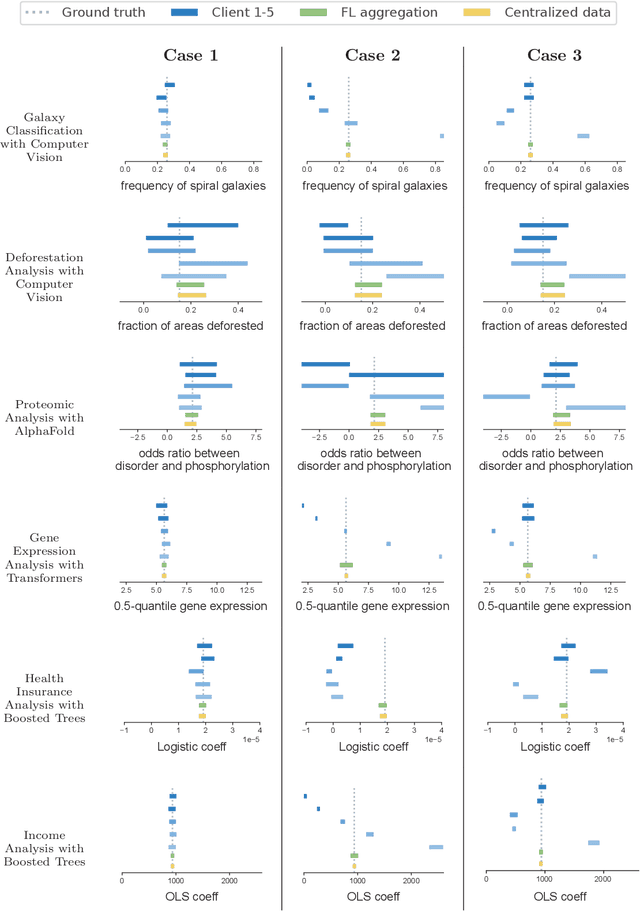
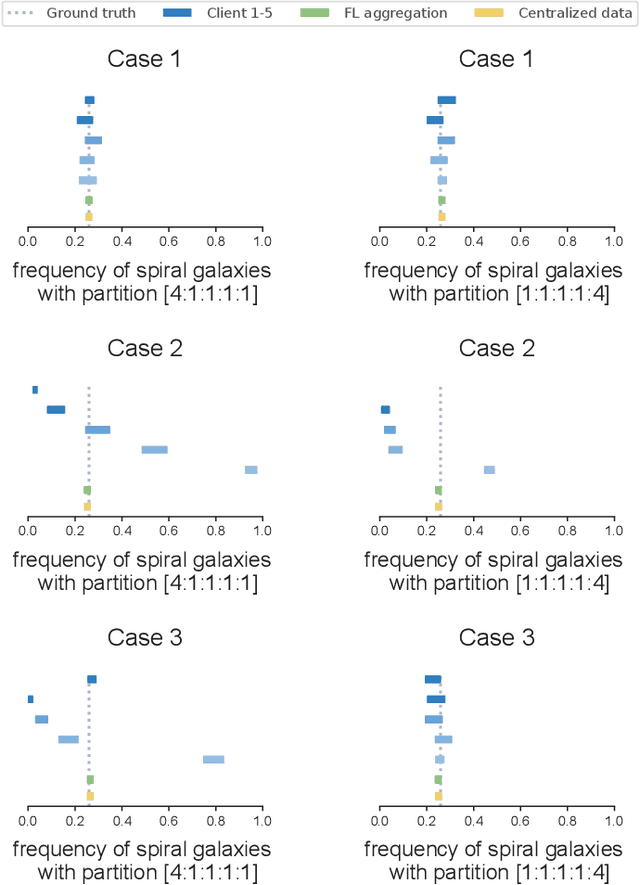
In various domains, the increasing application of machine learning allows researchers to access inexpensive predictive data, which can be utilized as auxiliary data for statistical inference. Although such data are often unreliable compared to gold-standard datasets, Prediction-Powered Inference (PPI) has been proposed to ensure statistical validity despite the unreliability. However, the challenge of `data silos' arises when the private gold-standard datasets are non-shareable for model training, leading to less accurate predictive models and invalid inferences. In this paper, we introduces the Federated Prediction-Powered Inference (Fed-PPI) framework, which addresses this challenge by enabling decentralized experimental data to contribute to statistically valid conclusions without sharing private information. The Fed-PPI framework involves training local models on private data, aggregating them through Federated Learning (FL), and deriving confidence intervals using PPI computation. The proposed framework is evaluated through experiments, demonstrating its effectiveness in producing valid confidence intervals.

Score-based Generative Models with Adaptive Momentum

Score-based generative models have demonstrated significant practical success in data-generating tasks. The models establish a diffusion process that perturbs the ground truth data to Gaussian noise and then learn the reverse process to transform noise into data. However, existing denoising methods such as Langevin dynamic and numerical stochastic differential equation solvers enjoy randomness but generate data slowly with a large number of score function evaluations, and the ordinary differential equation solvers enjoy faster sampling speed but no randomness may influence the sample quality. To this end, motivated by the Stochastic Gradient Descent (SGD) optimization methods and the high connection between the model sampling process with the SGD, we propose adaptive momentum sampling to accelerate the transforming process without introducing additional hyperparameters. Theoretically, we proved our method promises convergence under given conditions. In addition, we empirically show that our sampler can produce more faithful images/graphs in small sampling steps with 2 to 5 times speed up and obtain competitive scores compared to the baselines on image and graph generation tasks.

Accelerating Federated Learning by Selecting Beneficial Herd of Local Gradients

Federated Learning (FL) is a distributed machine learning framework in communication network systems. However, the systems' Non-Independent and Identically Distributed (Non-IID) data negatively affect the convergence efficiency of the global model, since only a subset of these data samples are beneficial for model convergence. In pursuit of this subset, a reliable approach involves determining a measure of validity to rank the samples within the dataset. In this paper, We propose the BHerd strategy which selects a beneficial herd of local gradients to accelerate the convergence of the FL model. Specifically, we map the distribution of the local dataset to the local gradients and use the Herding strategy to obtain a permutation of the set of gradients, where the more advanced gradients in the permutation are closer to the average of the set of gradients. These top portion of the gradients will be selected and sent to the server for global aggregation. We conduct experiments on different datasets, models and scenarios by building a prototype system, and experimental results demonstrate that our BHerd strategy is effective in selecting beneficial local gradients to mitigate the effects brought by the Non-IID dataset, thus accelerating model convergence.

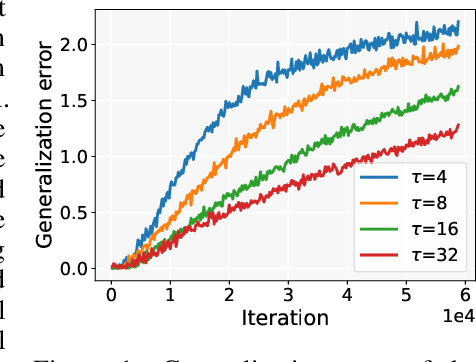
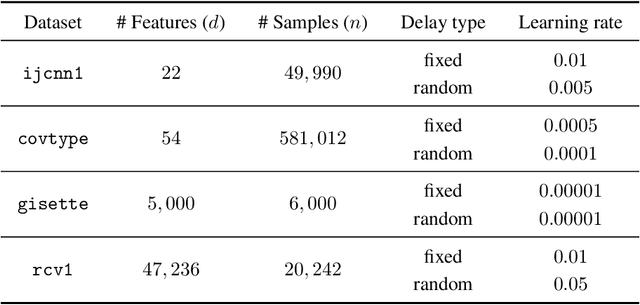
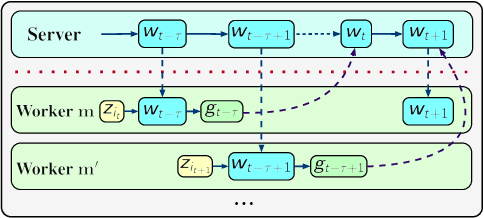
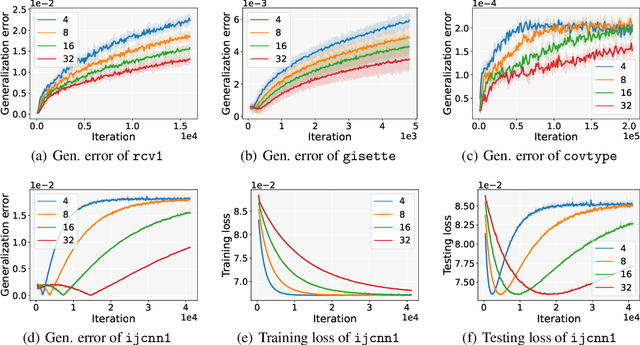
Towards Understanding the Generalizability of Delayed Stochastic Gradient Descent

Stochastic gradient descent (SGD) performed in an asynchronous manner plays a crucial role in training large-scale machine learning models. However, the generalization performance of asynchronous delayed SGD, which is an essential metric for assessing machine learning algorithms, has rarely been explored. Existing generalization error bounds are rather pessimistic and cannot reveal the correlation between asynchronous delays and generalization. In this paper, we investigate sharper generalization error bound for SGD with asynchronous delay $\tau$. Leveraging the generating function analysis tool, we first establish the average stability of the delayed gradient algorithm. Based on this algorithmic stability, we provide upper bounds on the generalization error of $\tilde{\mathcal{O}}(\frac{T-\tau}{n\tau})$ and $\tilde{\mathcal{O}}(\frac{1}{n})$ for quadratic convex and strongly convex problems, respectively, where $T$ refers to the iteration number and $n$ is the amount of training data. Our theoretical results indicate that asynchronous delays reduce the generalization error of the delayed SGD algorithm. Analogous analysis can be generalized to the random delay setting, and the experimental results validate our theoretical findings.

S2 Reducer: High-Performance Sparse Communication to Accelerate Distributed Deep Learning

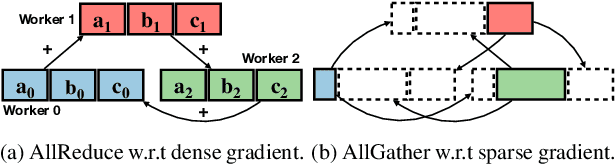
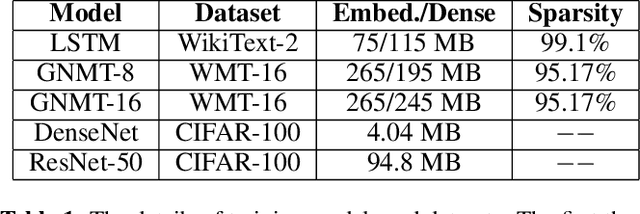
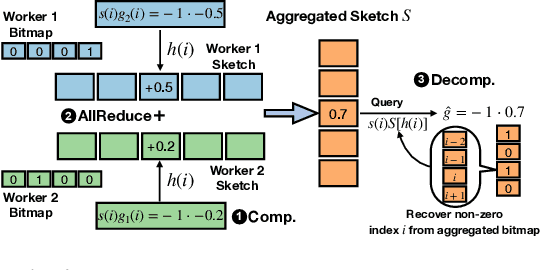
Distributed stochastic gradient descent (SGD) approach has been widely used in large-scale deep learning, and the gradient collective method is vital to ensure the training scalability of the distributed deep learning system. Collective communication such as AllReduce has been widely adopted for the distributed SGD process to reduce the communication time. However, AllReduce incurs large bandwidth resources while most gradients are sparse in many cases since many gradient values are zeros and should be efficiently compressed for bandwidth saving. To reduce the sparse gradient communication overhead, we propose Sparse-Sketch Reducer (S2 Reducer), a novel sketch-based sparse gradient aggregation method with convergence guarantees. S2 Reducer reduces the communication cost by only compressing the non-zero gradients with count-sketch and bitmap, and enables the efficient AllReduce operators for parallel SGD training. We perform extensive evaluation against four state-of-the-art methods over five training models. Our results show that S2 Reducer converges to the same accuracy, reduces 81\% sparse communication overhead, and achieves 1.8$ \times $ speedup compared to state-of-the-art approaches.