Discovering Common Information in Multi-view Data

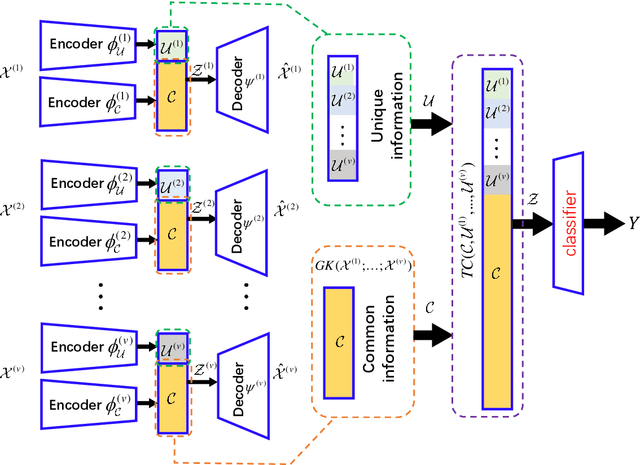
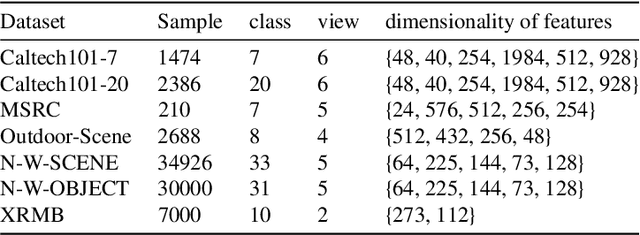
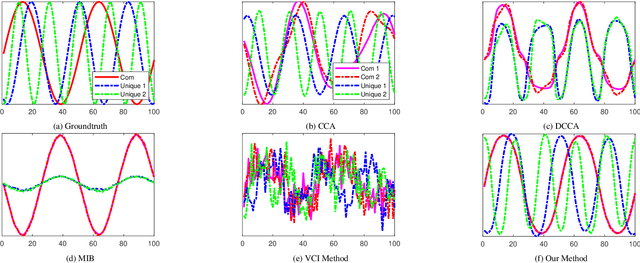
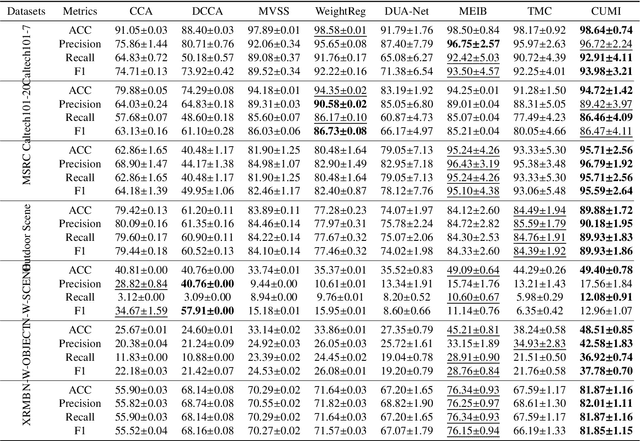
We introduce an innovative and mathematically rigorous definition for computing common information from multi-view data, drawing inspiration from G\'acs-K\"orner common information in information theory. Leveraging this definition, we develop a novel supervised multi-view learning framework to capture both common and unique information. By explicitly minimizing a total correlation term, the extracted common information and the unique information from each view are forced to be independent of each other, which, in turn, theoretically guarantees the effectiveness of our framework. To estimate information-theoretic quantities, our framework employs matrix-based R{\'e}nyi's $\alpha$-order entropy functional, which forgoes the need for variational approximation and distributional estimation in high-dimensional space. Theoretical proof is provided that our framework can faithfully discover both common and unique information from multi-view data. Experiments on synthetic and seven benchmark real-world datasets demonstrate the superior performance of our proposed framework over state-of-the-art approaches.

Generalized Cauchy-Schwarz Divergence and Its Deep Learning Applications

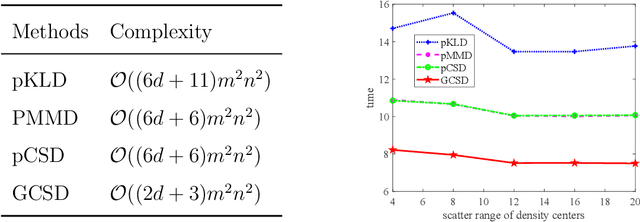
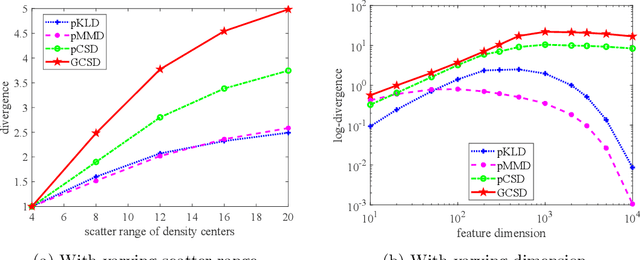
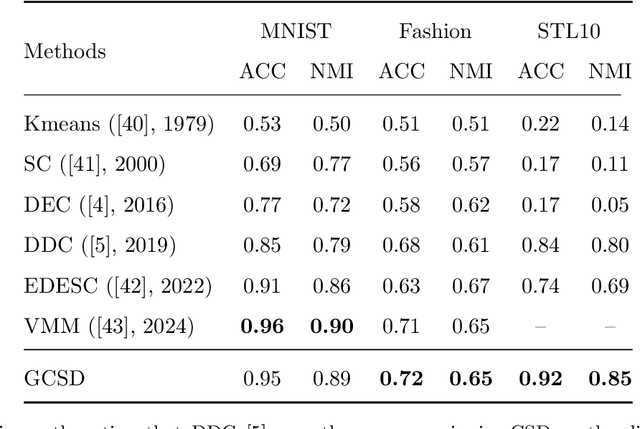
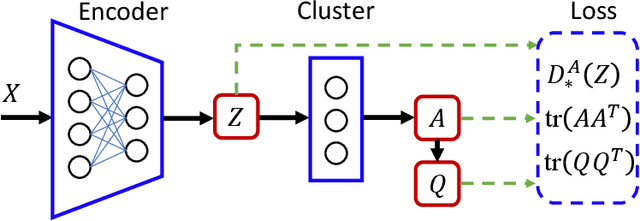
Divergence measures play a central role in machine learning and become increasingly essential in deep learning. However, valid and computationally efficient divergence measures for multiple (more than two) distributions are scarcely investigated. This becomes particularly crucial in areas where the simultaneous management of multiple distributions is both unavoidable and essential. Examples include clustering, multi-source domain adaptation or generalization, and multi-view learning, among others. Although calculating the mean of pairwise distances between any two distributions serves as a common way to quantify the total divergence among multiple distributions, it is crucial to acknowledge that this approach is not straightforward and requires significant computational resources. In this study, we introduce a new divergence measure for multiple distributions named the generalized Cauchy-Schwarz divergence (GCSD), which is inspired by the classic Cauchy-Schwarz divergence. Additionally, we provide a closed-form sample estimator based on kernel density estimation, making it convenient and straightforward to use in various machine-learning applications. Finally, we apply the proposed GCSD to two challenging machine learning tasks, namely deep learning-based clustering and the problem of multi-source domain adaptation. The experimental results showcase the impressive performance of GCSD in both tasks, highlighting its potential application in machine-learning areas that involve quantifying multiple distributions.

On the Adversarial Robustness of Generative Autoencoders in the Latent Space

The generative autoencoders, such as the variational autoencoders or the adversarial autoencoders, have achieved great success in lots of real-world applications, including image generation, and signal communication. However, little concern has been devoted to their robustness during practical deployment. Due to the probabilistic latent structure, variational autoencoders (VAEs) may confront problems such as a mismatch between the posterior distribution of the latent and real data manifold, or discontinuity in the posterior distribution of the latent. This leaves a back door for malicious attackers to collapse VAEs from the latent space, especially in scenarios where the encoder and decoder are used separately, such as communication and compressed sensing. In this work, we provide the first study on the adversarial robustness of generative autoencoders in the latent space. Specifically, we empirically demonstrate the latent vulnerability of popular generative autoencoders through attacks in the latent space. We also evaluate the difference between variational autoencoders and their deterministic variants and observe that the latter performs better in latent robustness. Meanwhile, we identify a potential trade-off between the adversarial robustness and the degree of the disentanglement of the latent codes. Additionally, we also verify the feasibility of improvement for the latent robustness of VAEs through adversarial training. In summary, we suggest concerning the adversarial latent robustness of the generative autoencoders, analyze several robustness-relative issues, and give some insights into a series of key challenges.