Deep Dynamic Probabilistic Canonical Correlation Analysis

This paper presents Deep Dynamic Probabilistic Canonical Correlation Analysis (D2PCCA), a model that integrates deep learning with probabilistic modeling to analyze nonlinear dynamical systems. Building on the probabilistic extensions of Canonical Correlation Analysis (CCA), D2PCCA captures nonlinear latent dynamics and supports enhancements such as KL annealing for improved convergence and normalizing flows for a more flexible posterior approximation. D2PCCA naturally extends to multiple observed variables, making it a versatile tool for encoding prior knowledge about sequential datasets and providing a probabilistic understanding of the system's dynamics. Experimental validation on real financial datasets demonstrates the effectiveness of D2PCCA and its extensions in capturing latent dynamics.

CondAmbigQA: A Benchmark and Dataset for Conditional Ambiguous Question Answering

Large language models (LLMs) are prone to hallucinations in question-answering (QA) tasks when faced with ambiguous questions. Users often assume that LLMs share their cognitive alignment, a mutual understanding of context, intent, and implicit details, leading them to omit critical information in the queries. However, LLMs generate responses based on assumptions that can misalign with user intent, which may be perceived as hallucinations if they misalign with the user's intent. Therefore, identifying those implicit assumptions is crucial to resolve ambiguities in QA. Prior work, such as AmbigQA, reduces ambiguity in queries via human-annotated clarifications, which is not feasible in real application. Meanwhile, ASQA compiles AmbigQA's short answers into long-form responses but inherits human biases and fails capture explicit logical distinctions that differentiates the answers. We introduce Conditional Ambiguous Question-Answering (CondAmbigQA), a benchmark with 200 ambiguous queries and condition-aware evaluation metrics. Our study pioneers the concept of ``conditions'' in ambiguous QA tasks, where conditions stand for contextual constraints or assumptions that resolve ambiguities. The retrieval-based annotation strategy uses retrieved Wikipedia fragments to identify possible interpretations for a given query as its conditions and annotate the answers through those conditions. Such a strategy minimizes human bias introduced by different knowledge levels among annotators. By fixing retrieval results, CondAmbigQA evaluates how RAG systems leverage conditions to resolve ambiguities. Experiments show that models considering conditions before answering improve performance by $20\%$, with an additional $5\%$ gain when conditions are explicitly provided. These results underscore the value of conditional reasoning in QA, offering researchers tools to rigorously evaluate ambiguity resolution.

Efficiently Integrate Large Language Models with Visual Perception: A Survey from the Training Paradigm Perspective

The integration of vision-language modalities has been a significant focus in multimodal learning, traditionally relying on Vision-Language Pretrained Models. However, with the advent of Large Language Models (LLMs), there has been a notable shift towards incorporating LLMs with vision modalities. Following this, the training paradigms for incorporating vision modalities into LLMs have evolved. Initially, the approach was to integrate the modalities through pretraining the modality integrator, named Single-stage Tuning. It has since branched out into methods focusing on performance enhancement, denoted as Two-stage Tuning, and those prioritizing parameter efficiency, referred to as Direct Adaptation. However, existing surveys primarily address the latest Vision Large Language Models (VLLMs) with Two-stage Tuning, leaving a gap in understanding the evolution of training paradigms and their unique parameter-efficient considerations. This paper categorizes and reviews 34 VLLMs from top conferences, journals, and highly cited Arxiv papers, focusing on parameter efficiency during adaptation from the training paradigm perspective. We first introduce the architecture of LLMs and parameter-efficient learning methods, followed by a discussion on vision encoders and a comprehensive taxonomy of modality integrators. We then review three training paradigms and their efficiency considerations, summarizing benchmarks in the VLLM field. To gain deeper insights into their effectiveness in parameter efficiency, we compare and discuss the experimental results of representative models, among which the experiment of the Direct Adaptation paradigm is replicated. Providing insights into recent developments and practical uses, this survey is a vital guide for researchers and practitioners navigating the efficient integration of vision modalities into LLMs.

Diffusion-based Method for Satellite Pattern-of-Life Identification

Satellite pattern-of-life (PoL) identification is crucial for space safety and satellite monitoring, involving the analysis of typical satellite behaviors such as station-keeping, drift, etc. However, existing PoL identification methods remain underdeveloped due to the complexity of aerospace systems, variability in satellite behaviors, and fluctuating observation sampling rates. In a first attempt, we developed a domain expertise-informed machine learning method (Expert-ML) to combine satellite orbital movement knowledge and machine learning models. The Expert-ML method achieved high accuracy results in simulation data and real-world data with normal sampling rate. However, this approach lacks of generality as it requires domain expertise and its performance degraded significantly when data sampling rate varied. To achieve generality, we propose a novel diffusion-based PoL identification method. Distinct from prior approaches, the proposed method leverages a diffusion model to achieve end-to-end identification without manual refinement or domain-specific knowledge. Specifically, we employ a multivariate time-series encoder to capture hidden representations of satellite positional data. The encoded features are subsequently incorporated as conditional information in the denoising process to generate PoL labels. Through experimentation across real-world satellite settings, our proposed diffusion-based method demonstrates its high identification quality and provides a robust solution even with reduced data sampling rates, indicating its great potential in practical satellite behavior pattern identification, tracking and related mission deployment.

Exploring ChatGPT-based Augmentation Strategies for Contrastive Aspect-based Sentiment Analysis

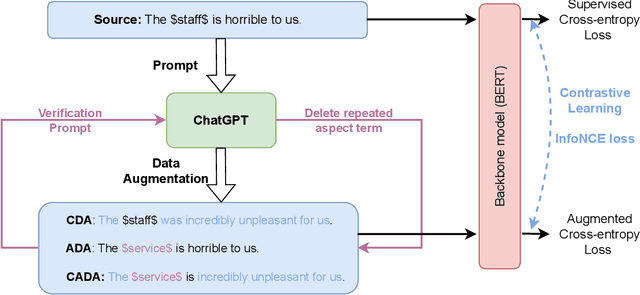
Aspect-based sentiment analysis (ABSA) involves identifying sentiment towards specific aspect terms in a sentence and allows us to uncover nuanced perspectives and attitudes on particular aspects of a product, service, or topic. However, the scarcity of labeled data poses a significant challenge to training high-quality models. To address this issue, we explore the potential of data augmentation using ChatGPT, a well-performing large language model (LLM), to enhance the sentiment classification performance towards aspect terms. Specifically, we explore three data augmentation strategies based on ChatGPT: context-focused, aspect-focused, and context-aspect data augmentation techniques. Context-focused data augmentation focuses on changing the word expression of context words in the sentence while keeping aspect terms unchanged. In contrast, aspect-focused data augmentation aims to change aspect terms but keep context words unchanged. Context-Aspect data augmentation integrates the above two data augmentations to generate augmented samples. Furthermore, we incorporate contrastive learning into the ABSA tasks to improve performance. Extensive experiments show that all three data augmentation techniques lead to performance improvements, with the context-aspect data augmentation strategy performing best and surpassing the performance of the baseline models.

Probabilistic Reduced-Dimensional Vector Autoregressive Modeling with Oblique Projections

In this paper, we propose a probabilistic reduced-dimensional vector autoregressive (PredVAR) model to extract low-dimensional dynamics from high-dimensional noisy data. The model utilizes an oblique projection to partition the measurement space into a subspace that accommodates the reduced-dimensional dynamics and a complementary static subspace. An optimal oblique decomposition is derived for the best predictability regarding prediction error covariance. Building on this, we develop an iterative PredVAR algorithm using maximum likelihood and the expectation-maximization (EM) framework. This algorithm alternately updates the estimates of the latent dynamics and optimal oblique projection, yielding dynamic latent variables with rank-ordered predictability and an explicit latent VAR model that is consistent with the outer projection model. The superior performance and efficiency of the proposed approach are demonstrated using data sets from a synthesized Lorenz system and an industrial process from Eastman Chemical.

MLPST: MLP is All You Need for Spatio-Temporal Prediction

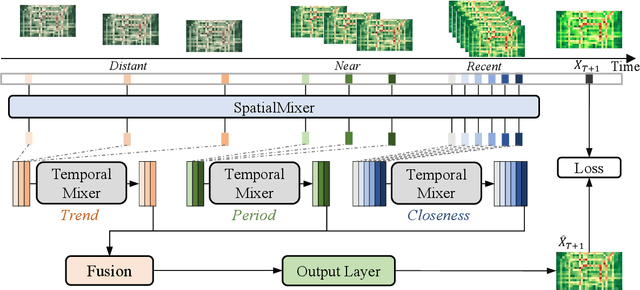
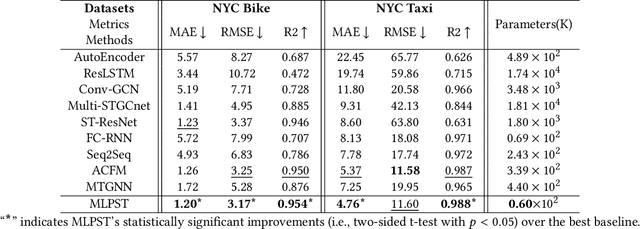
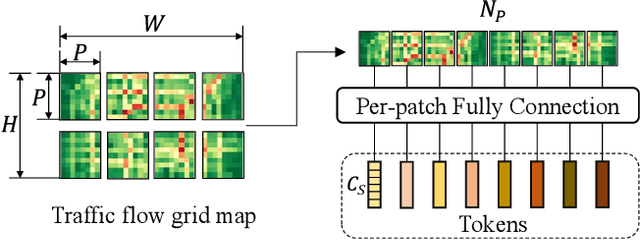
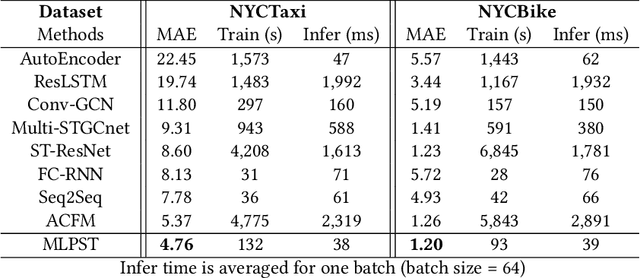
Traffic prediction is a typical spatio-temporal data mining task and has great significance to the public transportation system. Considering the demand for its grand application, we recognize key factors for an ideal spatio-temporal prediction method: efficient, lightweight, and effective. However, the current deep model-based spatio-temporal prediction solutions generally own intricate architectures with cumbersome optimization, which can hardly meet these expectations. To accomplish the above goals, we propose an intuitive and novel framework, MLPST, a pure multi-layer perceptron architecture for traffic prediction. Specifically, we first capture spatial relationships from both local and global receptive fields. Then, temporal dependencies in different intervals are comprehensively considered. Through compact and swift MLP processing, MLPST can well capture the spatial and temporal dependencies while requiring only linear computational complexity, as well as model parameters that are more than an order of magnitude lower than baselines. Extensive experiments validated the superior effectiveness and efficiency of MLPST against advanced baselines, and among models with optimal accuracy, MLPST achieves the best time and space efficiency.

On the Convergence of the Dynamic Inner PCA Algorithm

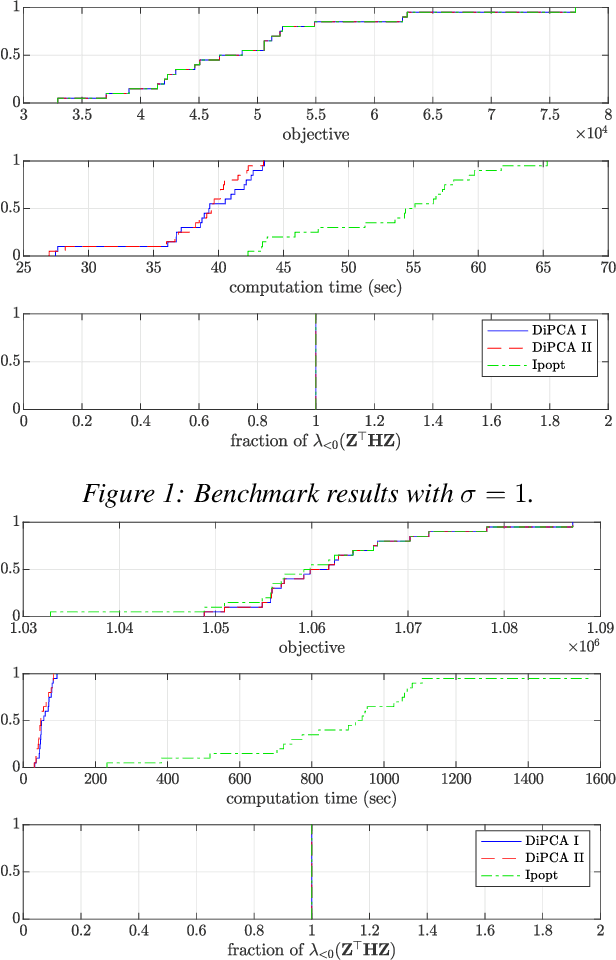
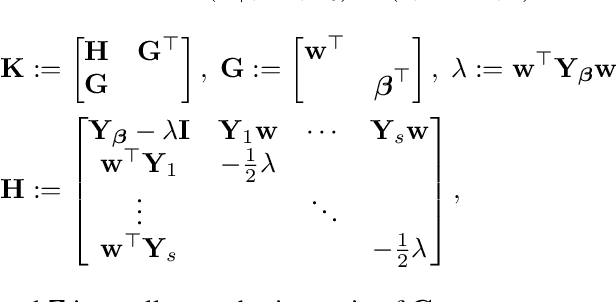
Dynamic inner principal component analysis (DiPCA) is a powerful method for the analysis of time-dependent multivariate data. DiPCA extracts dynamic latent variables that capture the most dominant temporal trends by solving a large-scale, dense, and nonconvex nonlinear program (NLP). A scalable decomposition algorithm has been recently proposed in the literature to solve these challenging NLPs. The decomposition algorithm performs well in practice but its convergence properties are not well understood. In this work, we show that this algorithm is a specialized variant of a coordinate maximization algorithm. This observation allows us to explain why the decomposition algorithm might work (or not) in practice and can guide improvements. We compare the performance of the decomposition strategies with that of the off-the-shelf solver Ipopt. The results show that decomposition is more scalable and, surprisingly, delivers higher quality solutions.