On the Convergence of the Dynamic Inner PCA Algorithm

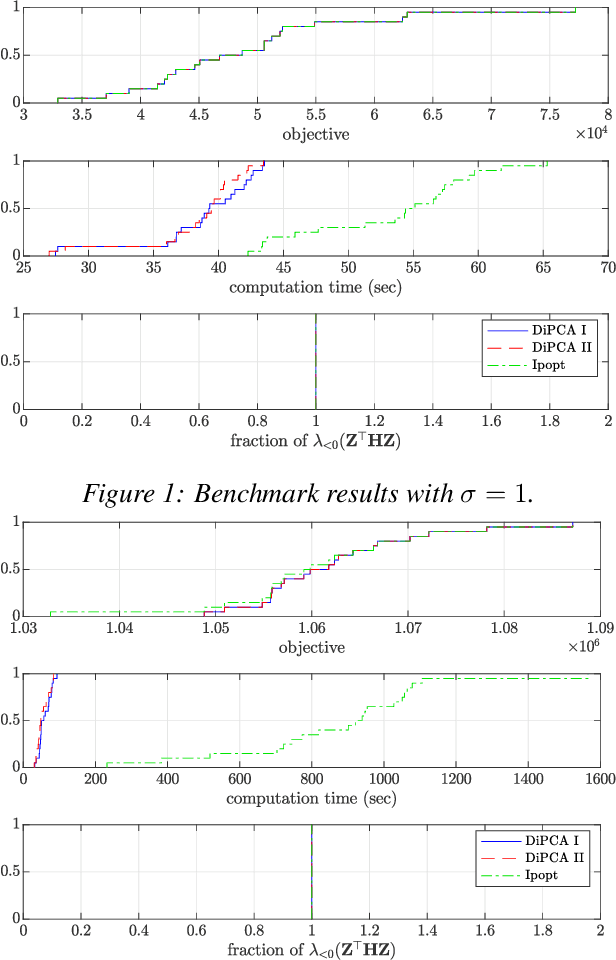
Dynamic inner principal component analysis (DiPCA) is a powerful method for the analysis of time-dependent multivariate data. DiPCA extracts dynamic latent variables that capture the most dominant temporal trends by solving a large-scale, dense, and nonconvex nonlinear program (NLP). A scalable decomposition algorithm has been recently proposed in the literature to solve these challenging NLPs. The decomposition algorithm performs well in practice but its convergence properties are not well understood. In this work, we show that this algorithm is a specialized variant of a coordinate maximization algorithm. This observation allows us to explain why the decomposition algorithm might work (or not) in practice and can guide improvements. We compare the performance of the decomposition strategies with that of the off-the-shelf solver Ipopt. The results show that decomposition is more scalable and, surprisingly, delivers higher quality solutions.