Victor M. Zavala
Department of Chemical and Biological Engineering, University of Wisconsin-Madison, Madison, USA
Physics-Constrained Machine Learning for Chemical Engineering
Aug 28, 2025Abstract:Physics-constrained machine learning (PCML) combines physical models with data-driven approaches to improve reliability, generalizability, and interpretability. Although PCML has shown significant benefits in diverse scientific and engineering domains, technical and intellectual challenges hinder its applicability in complex chemical engineering applications. Key difficulties include determining the amount and type of physical knowledge to embed, designing effective fusion strategies with ML, scaling models to large datasets and simulators, and quantifying predictive uncertainty. This perspective summarizes recent developments and highlights challenges/opportunities in applying PCML to chemical engineering, emphasizing on closed-loop experimental design, real-time dynamics and control, and handling of multi-scale phenomena.
A Digital Twin Simulator of a Pastillation Process with Applications to Automatic Control based on Computer Vision
Mar 18, 2025Abstract:We present a digital-twin simulator for a pastillation process. The simulation framework produces realistic thermal image data of the process that is used to train computer vision-based soft sensors based on convolutional neural networks (CNNs); the soft sensors produce output signals for temperature and product flow rate that enable real-time monitoring and feedback control. Pastillation technologies are high-throughput devices that are used in a broad range of industries; these processes face operational challenges such as real-time identification of clog locations (faults) in the rotating shell and the automatic, real-time adjustment of conveyor belt speed and operating conditions to stabilize output. The proposed simulator is able to capture this behavior and generates realistic data that can be used to benchmark different algorithms for image processing and different control architectures. We present a case study to illustrate the capabilities; the study explores behavior over a range of equipment sizes, clog locations, and clog duration. A feedback controller (tuned using Bayesian optimization) is used to adjust the conveyor belt speed based on the CNN output signal to achieve the desired process outputs.
On the Implementation of a Bayesian Optimization Framework for Interconnected Systems
Jan 01, 2025



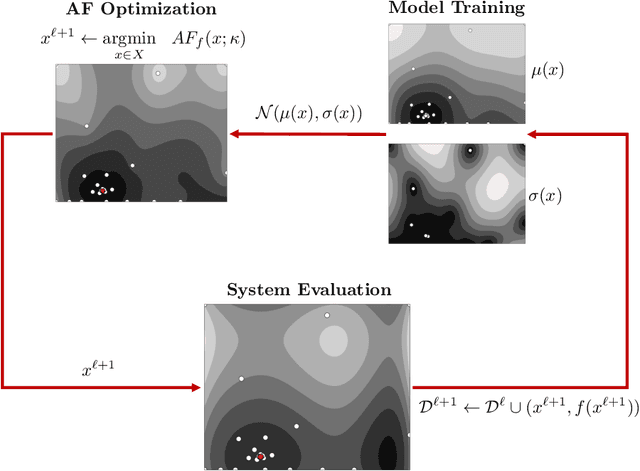
Abstract:Bayesian optimization (BO) is an effective paradigm for the optimization of expensive-to-sample systems. Standard BO learns the performance of a system $f(x)$ by using a Gaussian Process (GP) model; this treats the system as a black-box and limits its ability to exploit available structural knowledge (e.g., physics and sparse interconnections in a complex system). Grey-box modeling, wherein the performance function is treated as a composition of known and unknown intermediate functions $f(x, y(x))$ (where $y(x)$ is a GP model) offers a solution to this limitation; however, generating an analytical probability density for $f$ from the Gaussian density of $y(x)$ is often an intractable problem (e.g., when $f$ is nonlinear). Previous work has handled this issue by using sampling techniques or by solving an auxiliary problem over an augmented space where the values of $y(x)$ are constrained by confidence intervals derived from the GP models; such solutions are computationally intensive. In this work, we provide a detailed implementation of a recently proposed grey-box BO paradigm, BOIS, that uses adaptive linearizations of $f$ to obtain analytical expressions for the statistical moments of the composite function. We show that the BOIS approach enables the exploitation of structural knowledge, such as that arising in interconnected systems as well as systems that embed multiple GP models and combinations of physics and GP models. We benchmark the effectiveness of BOIS against standard BO and existing grey-box BO algorithms using a pair of case studies focused on chemical process optimization and design. Our results indicate that BOIS performs as well as or better than existing grey-box methods, while also being less computationally intensive.
BOIS: Bayesian Optimization of Interconnected Systems
Nov 29, 2023Abstract:Bayesian optimization (BO) has proven to be an effective paradigm for the global optimization of expensive-to-sample systems. One of the main advantages of BO is its use of Gaussian processes (GPs) to characterize model uncertainty which can be leveraged to guide the learning and search process. However, BO typically treats systems as black-boxes and this limits the ability to exploit structural knowledge (e.g., physics and sparse interconnections). Composite functions of the form $f(x, y(x))$, wherein GP modeling is shifted from the performance function $f$ to an intermediate function $y$, offer an avenue for exploiting structural knowledge. However, the use of composite functions in a BO framework is complicated by the need to generate a probability density for $f$ from the Gaussian density of $y$ calculated by the GP (e.g., when $f$ is nonlinear it is not possible to obtain a closed-form expression). Previous work has handled this issue using sampling techniques; these are easy to implement and flexible but are computationally intensive. In this work, we introduce a new paradigm which allows for the efficient use of composite functions in BO; this uses adaptive linearizations of $f$ to obtain closed-form expressions for the statistical moments of the composite function. We show that this simple approach (which we call BOIS) enables the exploitation of structural knowledge, such as that arising in interconnected systems as well as systems that embed multiple GP models and combinations of physics and GP models. Using a chemical process optimization case study, we benchmark the effectiveness of BOIS against standard BO and sampling approaches. Our results indicate that BOIS achieves performance gains and accurately captures the statistics of composite functions.
Uncertainty Quantification for Molecular Property Predictions with Graph Neural Architecture Search
Jul 19, 2023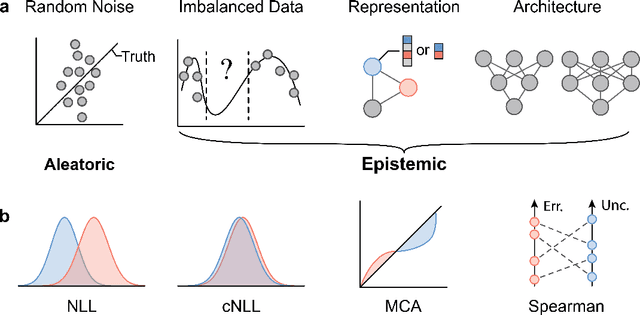

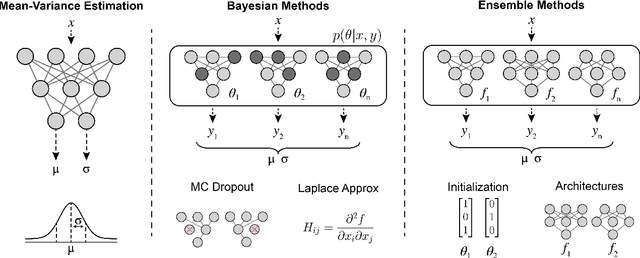
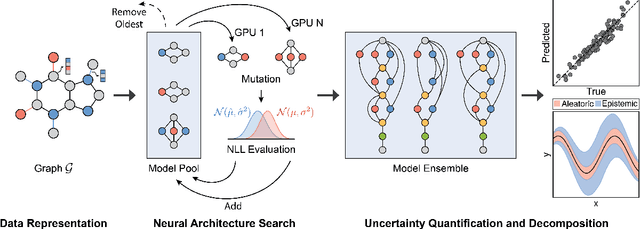
Abstract:Graph Neural Networks (GNNs) have emerged as a prominent class of data-driven methods for molecular property prediction. However, a key limitation of typical GNN models is their inability to quantify uncertainties in the predictions. This capability is crucial for ensuring the trustworthy use and deployment of models in downstream tasks. To that end, we introduce AutoGNNUQ, an automated uncertainty quantification (UQ) approach for molecular property prediction. AutoGNNUQ leverages architecture search to generate an ensemble of high-performing GNNs, enabling the estimation of predictive uncertainties. Our approach employs variance decomposition to separate data (aleatoric) and model (epistemic) uncertainties, providing valuable insights for reducing them. In our computational experiments, we demonstrate that AutoGNNUQ outperforms existing UQ methods in terms of both prediction accuracy and UQ performance on multiple benchmark datasets. Additionally, we utilize t-SNE visualization to explore correlations between molecular features and uncertainty, offering insight for dataset improvement. AutoGNNUQ has broad applicability in domains such as drug discovery and materials science, where accurate uncertainty quantification is crucial for decision-making.
A Graph-Based Modeling Framework for Tracing Hydrological Pollutant Transport in Surface Waters
Feb 10, 2023Abstract:Anthropogenic pollution of hydrological systems affects diverse communities and ecosystems around the world. Data analytics and modeling tools play a key role in fighting this challenge, as they can help identify key sources as well as trace transport and quantify impact within complex hydrological systems. Several tools exist for simulating and tracing pollutant transport throughout surface waters using detailed physical models; these tools are powerful, but can be computationally intensive, require significant amounts of data to be developed, and require expert knowledge for their use (ultimately limiting application scope). In this work, we present a graph modeling framework -- which we call ${\tt HydroGraphs}$ -- for understanding pollutant transport and fate across waterbodies, rivers, and watersheds. This framework uses a simplified representation of hydrological systems that can be constructed based purely on open-source data (National Hydrography Dataset and Watershed Boundary Dataset). The graph representation provides an flexible intuitive approach for capturing connectivity and for identifying upstream pollutant sources and for tracing downstream impacts within small and large hydrological systems. Moreover, the graph representation can facilitate the use of advanced algorithms and tools of graph theory, topology, optimization, and machine learning to aid data analytics and decision-making. We demonstrate the capabilities of our framework by using case studies in the State of Wisconsin; here, we aim to identify upstream nutrient pollutant sources that arise from agricultural practices and trace downstream impacts to waterbodies, rivers, and streams. Our tool ultimately seeks to help stakeholders design effective pollution prevention/mitigation practices and evaluate how surface waters respond to such practices.
Convolutional Neural Networks: Basic Concepts and Applications in Manufacturing
Oct 14, 2022

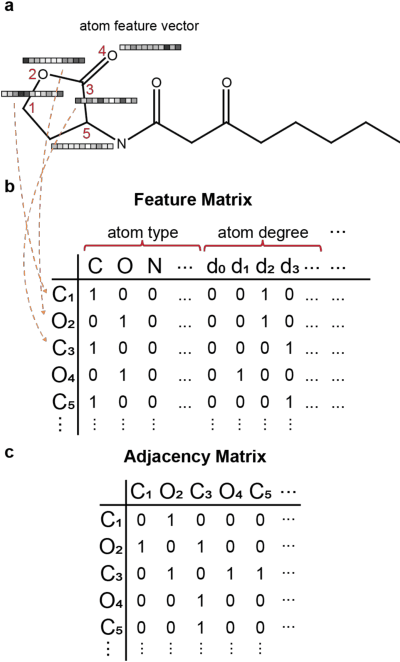
Abstract:We discuss basic concepts of convolutional neural networks (CNNs) and outline uses in manufacturing. We begin by discussing how different types of data objects commonly encountered in manufacturing (e.g., time series, images, micrographs, videos, spectra, molecular structures) can be represented in a flexible manner using tensors and graphs. We then discuss how CNNs use convolution operations to extract informative features (e.g., geometric patterns and textures) from the such representations to predict emergent properties and phenomena and/or to identify anomalies. We also discuss how CNNs can exploit color as a key source of information, which enables the use of modern computer vision hardware (e.g., infrared, thermal, and hyperspectral cameras). We illustrate the concepts using diverse case studies arising in spectral analysis, molecule design, sensor design, image-based control, and multivariate process monitoring.
New Paradigms for Exploiting Parallel Experiments in Bayesian Optimization
Oct 04, 2022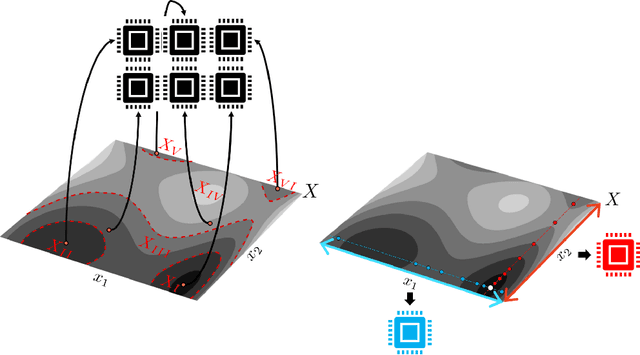
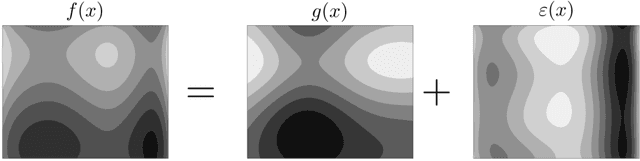
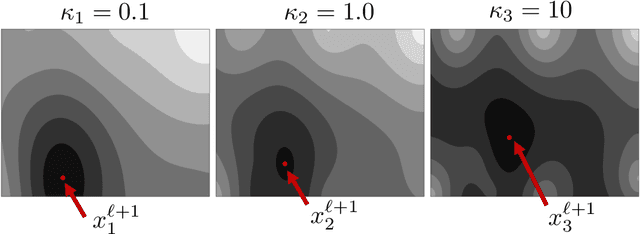
Abstract:Bayesian optimization (BO) is one of the most effective methods for closed-loop experimental design and black-box optimization. However, a key limitation of BO is that it is an inherently sequential algorithm (one experiment is proposed per round) and thus cannot directly exploit high-throughput (parallel) experiments. Diverse modifications to the BO framework have been proposed in the literature to enable exploitation of parallel experiments but such approaches are limited in the degree of parallelization that they can achieve and can lead to redundant experiments (thus wasting resources and potentially compromising performance). In this work, we present new parallel BO paradigms that exploit the structure of the system to partition the design space. Specifically, we propose an approach that partitions the design space by following the level sets of the performance function and an approach that exploits partially-separable structures of the performance function found. We conduct extensive numerical experiments using a reactor case study to benchmark the effectiveness of these approaches against a variety of state-of-the-art parallel algorithms reported in the literature. Our computational results show that our approaches significantly reduce the required search time and increase the probability of finding a global (rather than local) solution.
SAFE-OCC: A Novelty Detection Framework for Convolutional Neural Network Sensors and its Application in Process Control
Feb 03, 2022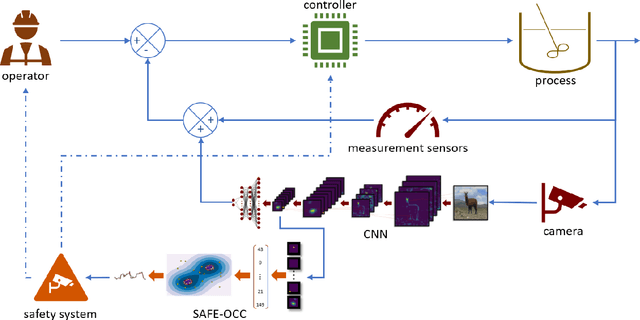



Abstract:We present a novelty detection framework for Convolutional Neural Network (CNN) sensors that we call Sensor-Activated Feature Extraction One-Class Classification (SAFE-OCC). We show that this framework enables the safe use of computer vision sensors in process control architectures. Emergent control applications use CNN models to map visual data to a state signal that can be interpreted by the controller. Incorporating such sensors introduces a significant system operation vulnerability because CNN sensors can exhibit high prediction errors when exposed to novel (abnormal) visual data. Unfortunately, identifying such novelties in real-time is nontrivial. To address this issue, the SAFE-OCC framework leverages the convolutional blocks of the CNN to create an effective feature space to conduct novelty detection using a desired one-class classification technique. This approach engenders a feature space that directly corresponds to that used by the CNN sensor and avoids the need to derive an independent latent space. We demonstrate the effectiveness of SAFE-OCC via simulated control environments.
Convolutional Neural Nets: Foundations, Computations, and New Applications
Jan 13, 2021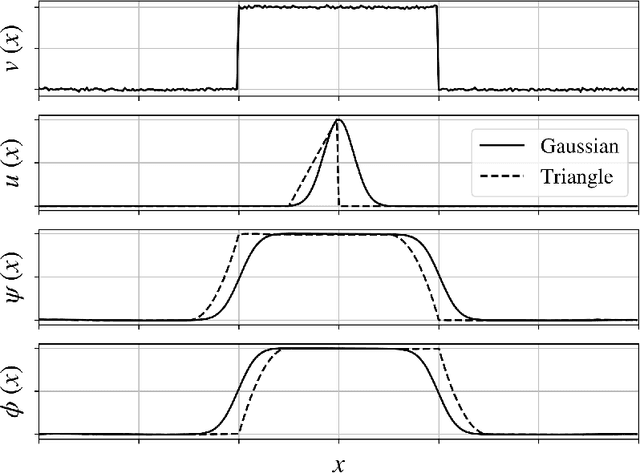

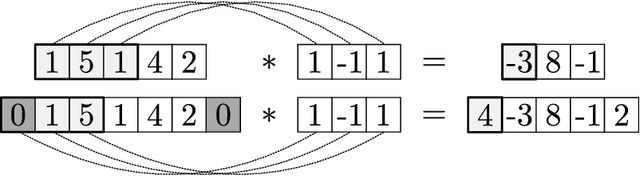
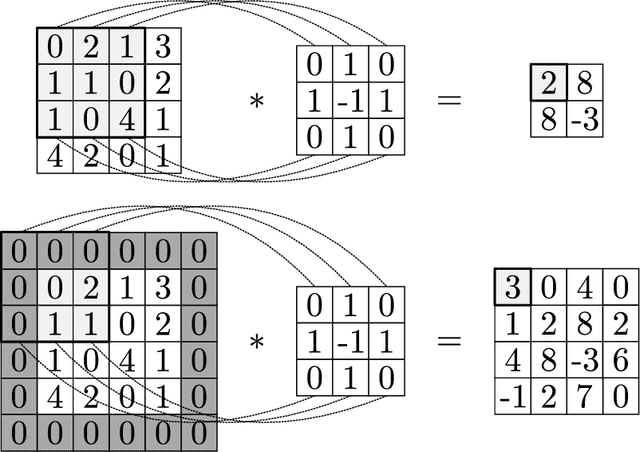
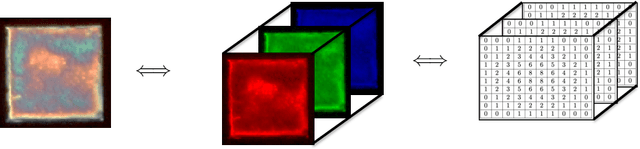
Abstract:We review mathematical foundations of convolutional neural nets (CNNs) with the goals of: i) highlighting connections with techniques from statistics, signal processing, linear algebra, differential equations, and optimization, ii) demystifying underlying computations, and iii) identifying new types of applications. CNNs are powerful machine learning models that highlight features from grid data to make predictions (regression and classification). The grid data object can be represented as vectors (in 1D), matrices (in 2D), or tensors (in 3D or higher dimensions) and can incorporate multiple channels (thus providing high flexibility in the input data representation). For example, an image can be represented as a 2D grid data object that contains red, green, and blue (RBG) channels (each channel is a 2D matrix). Similarly, a video can be represented as a 3D grid data object (two spatial dimensions plus time) with RGB channels (each channel is a 3D tensor). CNNs highlight features from the grid data by performing convolution operations with different types of operators. The operators highlight different types of features (e.g., patterns, gradients, geometrical features) and are learned by using optimization techniques. In other words, CNNs seek to identify optimal operators that best map the input data to the output data. A common misconception is that CNNs are only capable of processing image or video data but their application scope is much wider; specifically, datasets encountered in diverse applications can be expressed as grid data. Here, we show how to apply CNNs to new types of applications such as optimal control, flow cytometry, multivariate process monitoring, and molecular simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge