A Digital Twin Simulator of a Pastillation Process with Applications to Automatic Control based on Computer Vision

We present a digital-twin simulator for a pastillation process. The simulation framework produces realistic thermal image data of the process that is used to train computer vision-based soft sensors based on convolutional neural networks (CNNs); the soft sensors produce output signals for temperature and product flow rate that enable real-time monitoring and feedback control. Pastillation technologies are high-throughput devices that are used in a broad range of industries; these processes face operational challenges such as real-time identification of clog locations (faults) in the rotating shell and the automatic, real-time adjustment of conveyor belt speed and operating conditions to stabilize output. The proposed simulator is able to capture this behavior and generates realistic data that can be used to benchmark different algorithms for image processing and different control architectures. We present a case study to illustrate the capabilities; the study explores behavior over a range of equipment sizes, clog locations, and clog duration. A feedback controller (tuned using Bayesian optimization) is used to adjust the conveyor belt speed based on the CNN output signal to achieve the desired process outputs.

Uncertainty Quantification for Molecular Property Predictions with Graph Neural Architecture Search

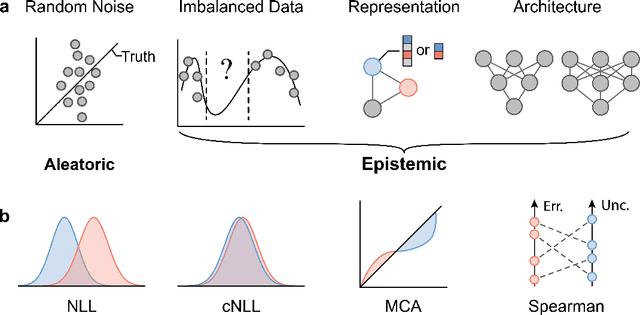
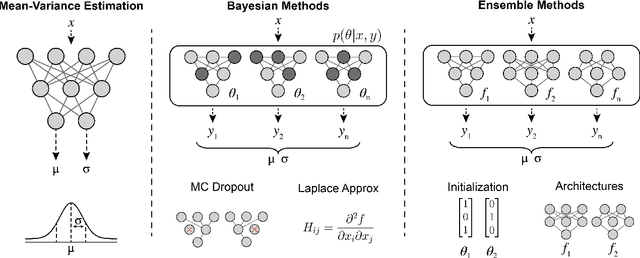
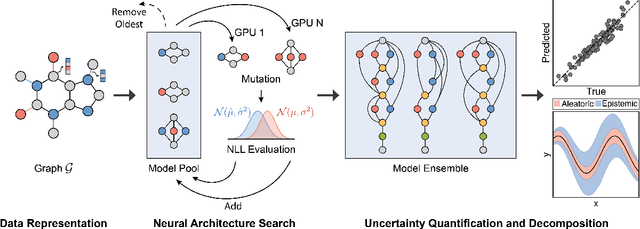
Graph Neural Networks (GNNs) have emerged as a prominent class of data-driven methods for molecular property prediction. However, a key limitation of typical GNN models is their inability to quantify uncertainties in the predictions. This capability is crucial for ensuring the trustworthy use and deployment of models in downstream tasks. To that end, we introduce AutoGNNUQ, an automated uncertainty quantification (UQ) approach for molecular property prediction. AutoGNNUQ leverages architecture search to generate an ensemble of high-performing GNNs, enabling the estimation of predictive uncertainties. Our approach employs variance decomposition to separate data (aleatoric) and model (epistemic) uncertainties, providing valuable insights for reducing them. In our computational experiments, we demonstrate that AutoGNNUQ outperforms existing UQ methods in terms of both prediction accuracy and UQ performance on multiple benchmark datasets. Additionally, we utilize t-SNE visualization to explore correlations between molecular features and uncertainty, offering insight for dataset improvement. AutoGNNUQ has broad applicability in domains such as drug discovery and materials science, where accurate uncertainty quantification is crucial for decision-making.

Convolutional Neural Networks: Basic Concepts and Applications in Manufacturing

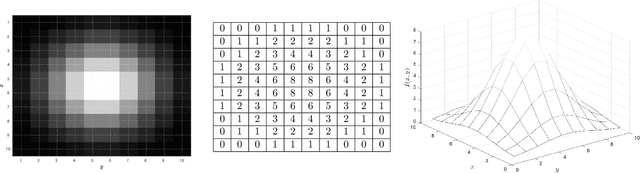
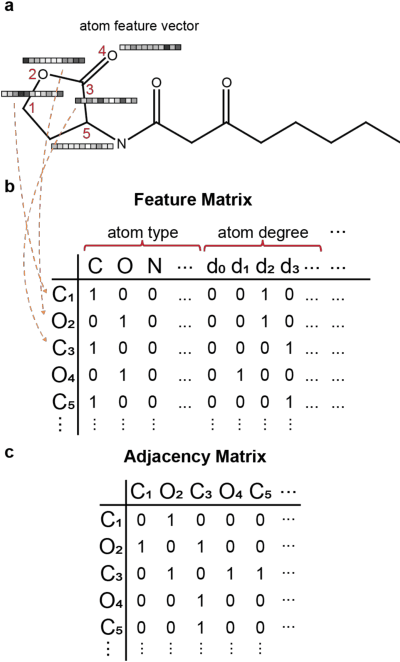
We discuss basic concepts of convolutional neural networks (CNNs) and outline uses in manufacturing. We begin by discussing how different types of data objects commonly encountered in manufacturing (e.g., time series, images, micrographs, videos, spectra, molecular structures) can be represented in a flexible manner using tensors and graphs. We then discuss how CNNs use convolution operations to extract informative features (e.g., geometric patterns and textures) from the such representations to predict emergent properties and phenomena and/or to identify anomalies. We also discuss how CNNs can exploit color as a key source of information, which enables the use of modern computer vision hardware (e.g., infrared, thermal, and hyperspectral cameras). We illustrate the concepts using diverse case studies arising in spectral analysis, molecule design, sensor design, image-based control, and multivariate process monitoring.

Convolutional Neural Nets: Foundations, Computations, and New Applications

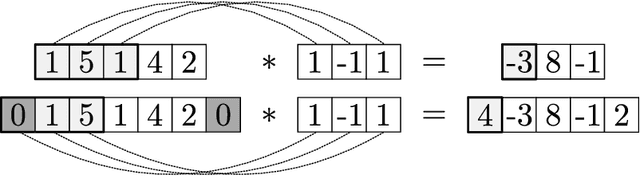
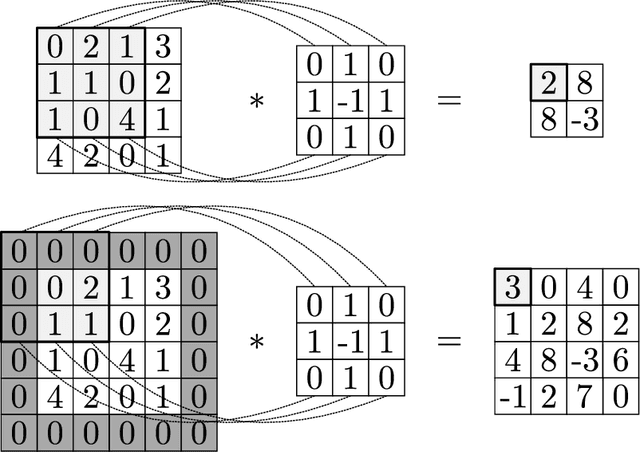
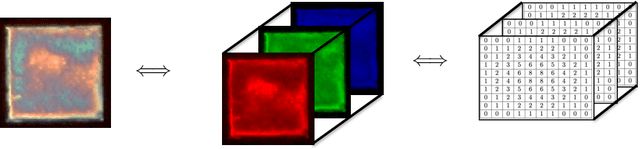
We review mathematical foundations of convolutional neural nets (CNNs) with the goals of: i) highlighting connections with techniques from statistics, signal processing, linear algebra, differential equations, and optimization, ii) demystifying underlying computations, and iii) identifying new types of applications. CNNs are powerful machine learning models that highlight features from grid data to make predictions (regression and classification). The grid data object can be represented as vectors (in 1D), matrices (in 2D), or tensors (in 3D or higher dimensions) and can incorporate multiple channels (thus providing high flexibility in the input data representation). For example, an image can be represented as a 2D grid data object that contains red, green, and blue (RBG) channels (each channel is a 2D matrix). Similarly, a video can be represented as a 3D grid data object (two spatial dimensions plus time) with RGB channels (each channel is a 3D tensor). CNNs highlight features from the grid data by performing convolution operations with different types of operators. The operators highlight different types of features (e.g., patterns, gradients, geometrical features) and are learned by using optimization techniques. In other words, CNNs seek to identify optimal operators that best map the input data to the output data. A common misconception is that CNNs are only capable of processing image or video data but their application scope is much wider; specifically, datasets encountered in diverse applications can be expressed as grid data. Here, we show how to apply CNNs to new types of applications such as optimal control, flow cytometry, multivariate process monitoring, and molecular simulations.

Graph Neural Network Architecture Search for Molecular Property Prediction

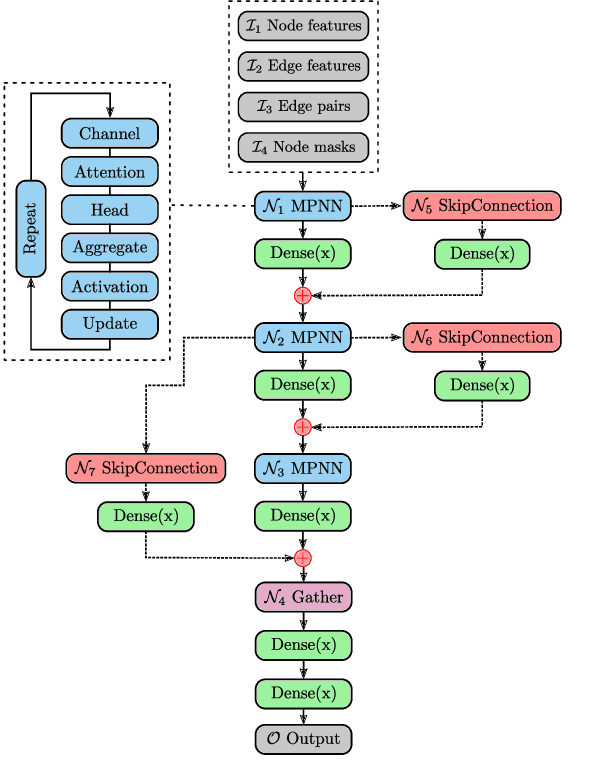
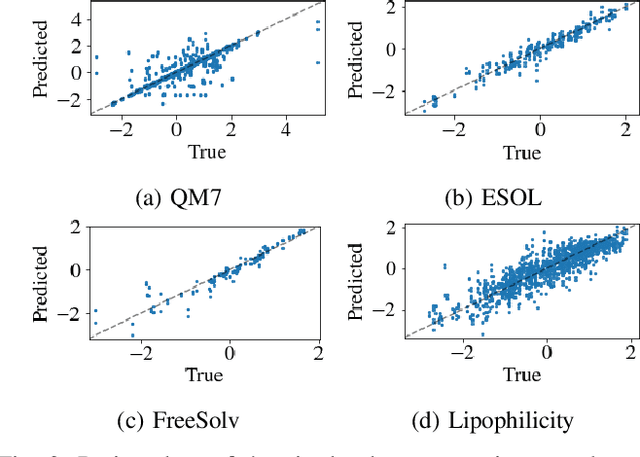
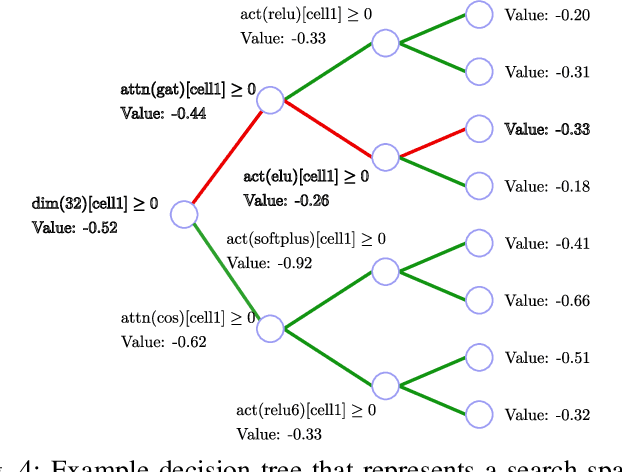
Predicting the properties of a molecule from its structure is a challenging task. Recently, deep learning methods have improved the state of the art for this task because of their ability to learn useful features from the given data. By treating molecule structure as graphs, where atoms and bonds are modeled as nodes and edges, graph neural networks (GNNs) have been widely used to predict molecular properties. However, the design and development of GNNs for a given data set rely on labor-intensive design and tuning of the network architectures. Neural architecture search (NAS) is a promising approach to discover high-performing neural network architectures automatically. To that end, we develop an NAS approach to automate the design and development of GNNs for molecular property prediction. Specifically, we focus on automated development of message-passing neural networks (MPNNs) to predict the molecular properties of small molecules in quantum mechanics and physical chemistry data sets from the MoleculeNet benchmark. We demonstrate the superiority of the automatically discovered MPNNs by comparing them with manually designed GNNs from the MoleculeNet benchmark. We study the relative importance of the choices in the MPNN search space, demonstrating that customizing the architecture is critical to enhancing performance in molecular property prediction and that the proposed approach can perform customization automatically with minimal manual effort.