Leonardo D. González
Department of Chemical & Biological Engineering, University of Wisconsin-Madison, Madison, USA
A Digital Twin Simulator of a Pastillation Process with Applications to Automatic Control based on Computer Vision
Mar 18, 2025Abstract:We present a digital-twin simulator for a pastillation process. The simulation framework produces realistic thermal image data of the process that is used to train computer vision-based soft sensors based on convolutional neural networks (CNNs); the soft sensors produce output signals for temperature and product flow rate that enable real-time monitoring and feedback control. Pastillation technologies are high-throughput devices that are used in a broad range of industries; these processes face operational challenges such as real-time identification of clog locations (faults) in the rotating shell and the automatic, real-time adjustment of conveyor belt speed and operating conditions to stabilize output. The proposed simulator is able to capture this behavior and generates realistic data that can be used to benchmark different algorithms for image processing and different control architectures. We present a case study to illustrate the capabilities; the study explores behavior over a range of equipment sizes, clog locations, and clog duration. A feedback controller (tuned using Bayesian optimization) is used to adjust the conveyor belt speed based on the CNN output signal to achieve the desired process outputs.
On the Implementation of a Bayesian Optimization Framework for Interconnected Systems
Jan 01, 2025



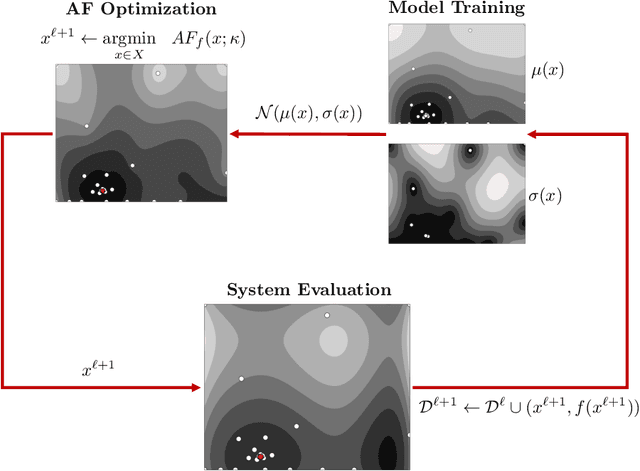
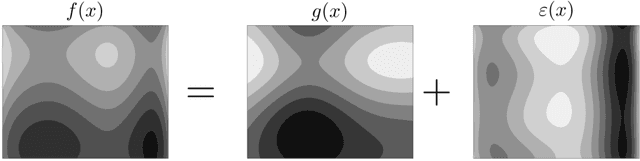
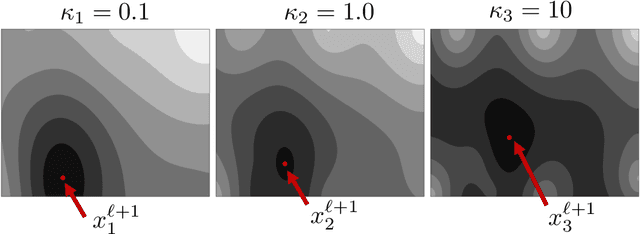
Abstract:Bayesian optimization (BO) is an effective paradigm for the optimization of expensive-to-sample systems. Standard BO learns the performance of a system $f(x)$ by using a Gaussian Process (GP) model; this treats the system as a black-box and limits its ability to exploit available structural knowledge (e.g., physics and sparse interconnections in a complex system). Grey-box modeling, wherein the performance function is treated as a composition of known and unknown intermediate functions $f(x, y(x))$ (where $y(x)$ is a GP model) offers a solution to this limitation; however, generating an analytical probability density for $f$ from the Gaussian density of $y(x)$ is often an intractable problem (e.g., when $f$ is nonlinear). Previous work has handled this issue by using sampling techniques or by solving an auxiliary problem over an augmented space where the values of $y(x)$ are constrained by confidence intervals derived from the GP models; such solutions are computationally intensive. In this work, we provide a detailed implementation of a recently proposed grey-box BO paradigm, BOIS, that uses adaptive linearizations of $f$ to obtain analytical expressions for the statistical moments of the composite function. We show that the BOIS approach enables the exploitation of structural knowledge, such as that arising in interconnected systems as well as systems that embed multiple GP models and combinations of physics and GP models. We benchmark the effectiveness of BOIS against standard BO and existing grey-box BO algorithms using a pair of case studies focused on chemical process optimization and design. Our results indicate that BOIS performs as well as or better than existing grey-box methods, while also being less computationally intensive.
BOIS: Bayesian Optimization of Interconnected Systems
Nov 29, 2023Abstract:Bayesian optimization (BO) has proven to be an effective paradigm for the global optimization of expensive-to-sample systems. One of the main advantages of BO is its use of Gaussian processes (GPs) to characterize model uncertainty which can be leveraged to guide the learning and search process. However, BO typically treats systems as black-boxes and this limits the ability to exploit structural knowledge (e.g., physics and sparse interconnections). Composite functions of the form $f(x, y(x))$, wherein GP modeling is shifted from the performance function $f$ to an intermediate function $y$, offer an avenue for exploiting structural knowledge. However, the use of composite functions in a BO framework is complicated by the need to generate a probability density for $f$ from the Gaussian density of $y$ calculated by the GP (e.g., when $f$ is nonlinear it is not possible to obtain a closed-form expression). Previous work has handled this issue using sampling techniques; these are easy to implement and flexible but are computationally intensive. In this work, we introduce a new paradigm which allows for the efficient use of composite functions in BO; this uses adaptive linearizations of $f$ to obtain closed-form expressions for the statistical moments of the composite function. We show that this simple approach (which we call BOIS) enables the exploitation of structural knowledge, such as that arising in interconnected systems as well as systems that embed multiple GP models and combinations of physics and GP models. Using a chemical process optimization case study, we benchmark the effectiveness of BOIS against standard BO and sampling approaches. Our results indicate that BOIS achieves performance gains and accurately captures the statistics of composite functions.
New Paradigms for Exploiting Parallel Experiments in Bayesian Optimization
Oct 04, 2022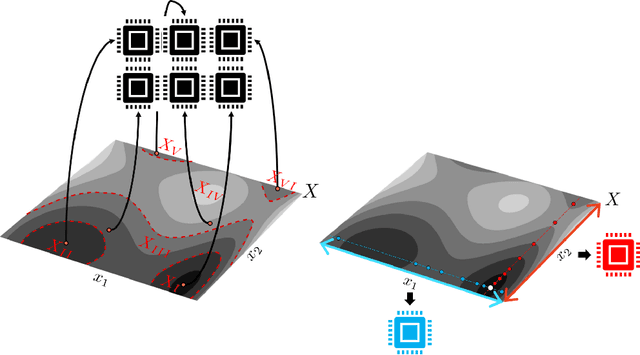
Abstract:Bayesian optimization (BO) is one of the most effective methods for closed-loop experimental design and black-box optimization. However, a key limitation of BO is that it is an inherently sequential algorithm (one experiment is proposed per round) and thus cannot directly exploit high-throughput (parallel) experiments. Diverse modifications to the BO framework have been proposed in the literature to enable exploitation of parallel experiments but such approaches are limited in the degree of parallelization that they can achieve and can lead to redundant experiments (thus wasting resources and potentially compromising performance). In this work, we present new parallel BO paradigms that exploit the structure of the system to partition the design space. Specifically, we propose an approach that partitions the design space by following the level sets of the performance function and an approach that exploits partially-separable structures of the performance function found. We conduct extensive numerical experiments using a reactor case study to benchmark the effectiveness of these approaches against a variety of state-of-the-art parallel algorithms reported in the literature. Our computational results show that our approaches significantly reduce the required search time and increase the probability of finding a global (rather than local) solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge