Contrastive Entropy Bounds for Density and Conditional Density Decomposition

This paper studies the interpretability of neural network features from a Bayesian Gaussian view, where optimizing a cost is reaching a probabilistic bound; learning a model approximates a density that makes the bound tight and the cost optimal, often with a Gaussian mixture density. The two examples are Mixture Density Networks (MDNs) using the bound for the marginal and autoencoders using the conditional bound. It is a known result, not only for autoencoders, that minimizing the error between inputs and outputs maximizes the dependence between inputs and the middle. We use Hilbert space and decomposition to address cases where a multiple-output network produces multiple centers defining a Gaussian mixture. Our first finding is that an autoencoder's objective is equivalent to maximizing the trace of a Gaussian operator, the sum of eigenvalues under bases orthonormal w.r.t. the data and model distributions. This suggests that, when a one-to-one correspondence as needed in autoencoders is unnecessary, we can instead maximize the nuclear norm of this operator, the sum of singular values, to maximize overall rank rather than trace. Thus the trace of a Gaussian operator can be used to train autoencoders, and its nuclear norm can be used as divergence to train MDNs. Our second test uses inner products and norms in a Hilbert space to define bounds and costs. Such bounds often have an extra norm compared to KL-based bounds, which increases sample diversity and prevents the trivial solution where a multiple-output network produces the same constant, at the cost of requiring a sample batch to estimate and optimize. We propose an encoder-mixture-decoder architecture whose decoder is multiple-output, producing multiple centers per sample, potentially tightening the bound. Assuming the data are small-variance Gaussian mixtures, this upper bound can be tracked and analyzed quantitatively.

A Simple and Effective Method for Uncertainty Quantification and OOD Detection

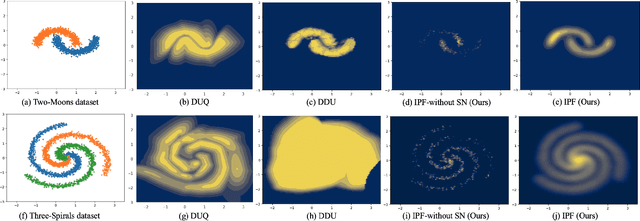
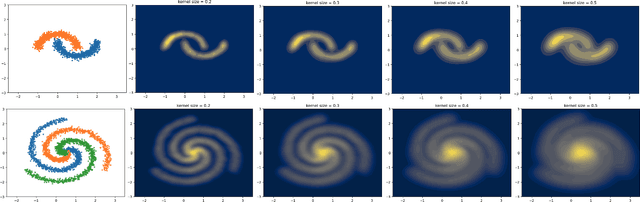
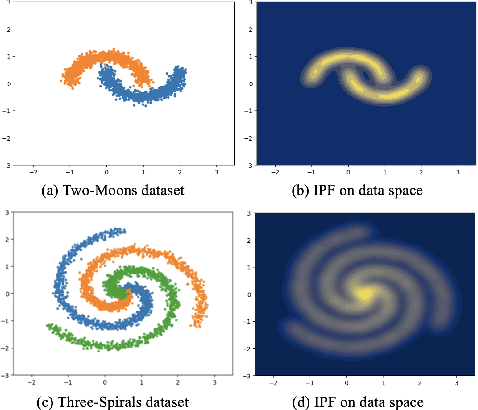
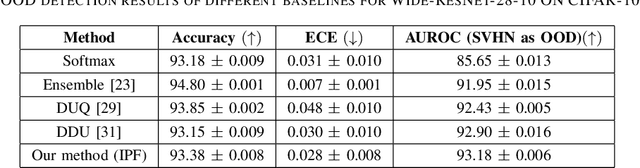
Bayesian neural networks and deep ensemble methods have been proposed for uncertainty quantification; however, they are computationally intensive and require large storage. By utilizing a single deterministic model, we can solve the above issue. We propose an effective method based on feature space density to quantify uncertainty for distributional shifts and out-of-distribution (OOD) detection. Specifically, we leverage the information potential field derived from kernel density estimation to approximate the feature space density of the training set. By comparing this density with the feature space representation of test samples, we can effectively determine whether a distributional shift has occurred. Experiments were conducted on a 2D synthetic dataset (Two Moons and Three Spirals) as well as an OOD detection task (CIFAR-10 vs. SVHN). The results demonstrate that our method outperforms baseline models.

Spectral Eigenfunction Decomposition for Kernel Adaptive Filtering

Kernel adaptive filtering (KAF) integrates traditional linear algorithms with kernel methods to generate nonlinear solutions in the input space. The standard approach relies on the representer theorem and the kernel trick to perform pairwise evaluations of a kernel function in place of the inner product, which leads to scalability issues for large datasets due to its linear and superlinear growth with respect to the size of the training data. Explicit features have been proposed to tackle this problem, exploiting the properties of the Gaussian-type kernel functions. These approximation methods address the implicitness and infinite dimensional representation of conventional kernel methods. However, achieving an accurate finite approximation for the kernel evaluation requires a sufficiently large vector representation for the dot products. An increase in the input-space dimension leads to a combinatorial explosion in the dimensionality of the explicit space, i.e., it trades one dimensionality problem (implicit, infinite dimensional RKHS) for another (curse of dimensionality). This paper introduces a construction that simultaneously solves these two problems in a principled way, by providing an explicit Euclidean representation of the RKHS while reducing its dimensionality. We present SPEctral Eigenfunction Decomposition (SPEED) along with an efficient incremental approach for fast calculation of the dominant kernel eigenbasis, which enables us to track the kernel eigenspace dynamically for adaptive filtering. Simulation results on chaotic time series prediction demonstrate this novel construction outperforms existing explicit kernel features with greater efficiency.

ELEMENT: Episodic and Lifelong Exploration via Maximum Entropy

This paper proposes \emph{Episodic and Lifelong Exploration via Maximum ENTropy} (ELEMENT), a novel, multiscale, intrinsically motivated reinforcement learning (RL) framework that is able to explore environments without using any extrinsic reward and transfer effectively the learned skills to downstream tasks. We advance the state of the art in three ways. First, we propose a multiscale entropy optimization to take care of the fact that previous maximum state entropy, for lifelong exploration with millions of state observations, suffers from vanishing rewards and becomes very expensive computationally across iterations. Therefore, we add an episodic maximum entropy over each episode to speedup the search further. Second, we propose a novel intrinsic reward for episodic entropy maximization named \emph{average episodic state entropy} which provides the optimal solution for a theoretical upper bound of the episodic state entropy objective. Third, to speed the lifelong entropy maximization, we propose a $k$ nearest neighbors ($k$NN) graph to organize the estimation of the entropy and updating processes that reduces the computation substantially. Our ELEMENT significantly outperforms state-of-the-art intrinsic rewards in both episodic and lifelong setups. Moreover, it can be exploited in task-agnostic pre-training, collecting data for offline reinforcement learning, etc.

Cauchy-Schwarz Divergence Information Bottleneck for Regression

The information bottleneck (IB) approach is popular to improve the generalization, robustness and explainability of deep neural networks. Essentially, it aims to find a minimum sufficient representation $\mathbf{t}$ by striking a trade-off between a compression term $I(\mathbf{x};\mathbf{t})$ and a prediction term $I(y;\mathbf{t})$, where $I(\cdot;\cdot)$ refers to the mutual information (MI). MI is for the IB for the most part expressed in terms of the Kullback-Leibler (KL) divergence, which in the regression case corresponds to prediction based on mean squared error (MSE) loss with Gaussian assumption and compression approximated by variational inference. In this paper, we study the IB principle for the regression problem and develop a new way to parameterize the IB with deep neural networks by exploiting favorable properties of the Cauchy-Schwarz (CS) divergence. By doing so, we move away from MSE-based regression and ease estimation by avoiding variational approximations or distributional assumptions. We investigate the improved generalization ability of our proposed CS-IB and demonstrate strong adversarial robustness guarantees. We demonstrate its superior performance on six real-world regression tasks over other popular deep IB approaches. We additionally observe that the solutions discovered by CS-IB always achieve the best trade-off between prediction accuracy and compression ratio in the information plane. The code is available at \url{https://github.com/SJYuCNEL/Cauchy-Schwarz-Information-Bottleneck}.

An Analytic Solution for Kernel Adaptive Filtering

Conventional kernel adaptive filtering (KAF) uses a prescribed, positive definite, nonlinear function to define the Reproducing Kernel Hilbert Space (RKHS), where the optimal solution for mean square error estimation is approximated using search techniques. Instead, this paper proposes to embed the full statistics of the input data in the kernel definition, obtaining the first analytical solution for nonlinear regression and nonlinear adaptive filtering applications. We call this solution the Functional Wiener Filter (FWF). Conceptually, the methodology is an extension of Parzen's work on the autocorrelation RKHS to nonlinear functional spaces. We provide an extended functional Wiener equation, and present a solution to this equation in an explicit, finite dimensional, data-dependent RKHS. We further explain the necessary requirements to compute the analytical solution in RKHS, which is beyond traditional methodologies based on the kernel trick. The FWF analytic solution to the nonlinear minimum mean square error problem has better accuracy than other kernel-based algorithms in synthetic, stationary data. In real world time series, it has comparable accuracy to KAF but displays constant complexity with respect to number of training samples. For evaluation, it is as computationally efficient as the Wiener solution (with a larger number of dimensions than the linear case). We also show how the difference equation learned by the FWF from data can be extracted leading to system identification applications, which extend the possible applications of the FWF beyond optimal nonlinear filtering.

Weakly-Supervised Semantic Segmentation of Circular-Scan, Synthetic-Aperture-Sonar Imagery

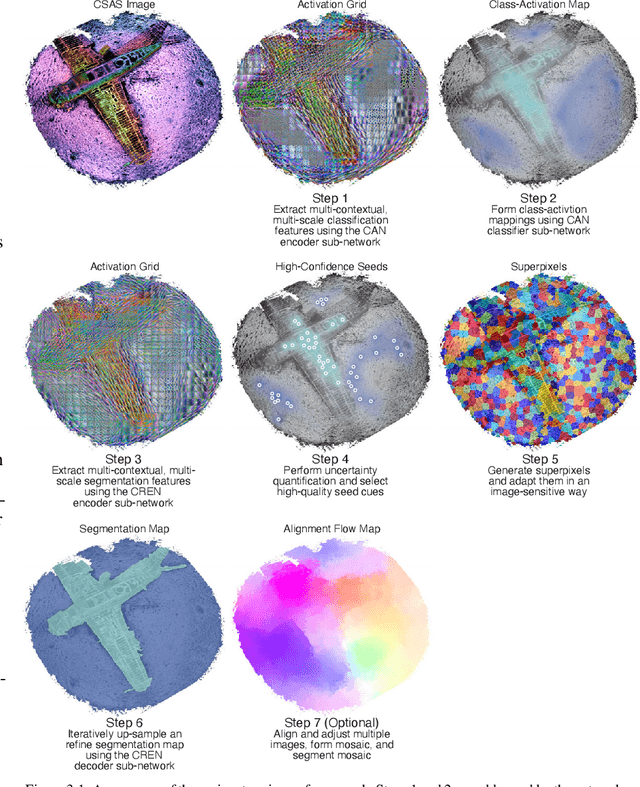
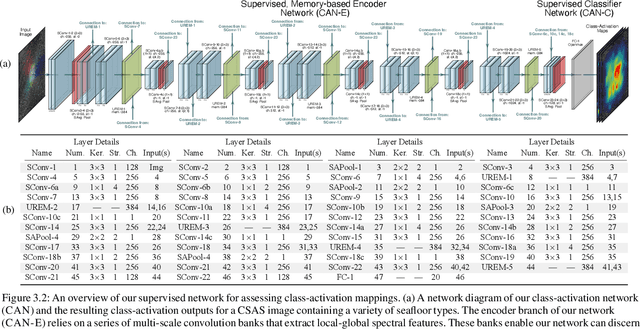
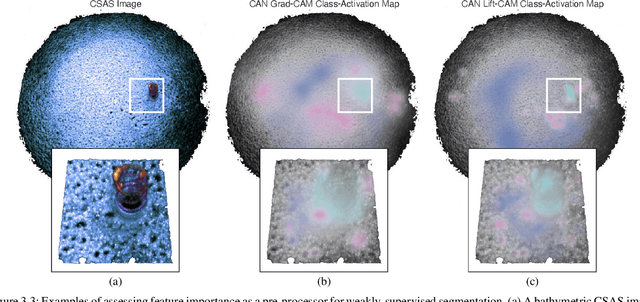
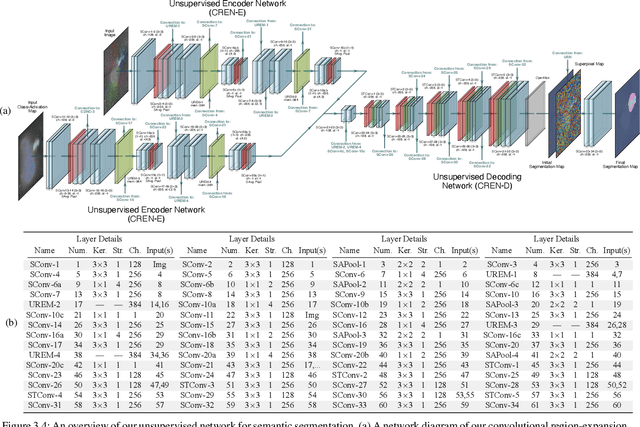
We propose a weakly-supervised framework for the semantic segmentation of circular-scan synthetic-aperture-sonar (CSAS) imagery. The first part of our framework is trained in a supervised manner, on image-level labels, to uncover a set of semi-sparse, spatially-discriminative regions in each image. The classification uncertainty of each region is then evaluated. Those areas with the lowest uncertainties are then chosen to be weakly labeled segmentation seeds, at the pixel level, for the second part of the framework. Each of the seed extents are progressively resized according to an unsupervised, information-theoretic loss with structured-prediction regularizers. This reshaping process uses multi-scale, adaptively-weighted features to delineate class-specific transitions in local image content. Content-addressable memories are inserted at various parts of our framework so that it can leverage features from previously seen images to improve segmentation performance for related images. We evaluate our weakly-supervised framework using real-world CSAS imagery that contains over ten seafloor classes and ten target classes. We show that our framework performs comparably to nine fully-supervised deep networks. Our framework also outperforms eleven of the best weakly-supervised deep networks. We achieve state-of-the-art performance when pre-training on natural imagery. The average absolute performance gap to the next-best weakly-supervised network is well over ten percent for both natural imagery and sonar imagery. This gap is found to be statistically significant.

An Alternate View on Optimal Filtering in an RKHS

Kernel Adaptive Filtering (KAF) are mathematically principled methods which search for a function in a Reproducing Kernel Hilbert Space. While they work well for tasks such as time series prediction and system identification they are plagued by a linear relationship between number of training samples and model size, hampering their use on the very large data sets common in today's data saturated world. Previous methods try to solve this issue by sparsification. We describe a novel view of optimal filtering which may provide a route towards solutions in a RKHS which do not necessarily have this linear growth in model size. We do this by defining a RKHS in which the time structure of a stochastic process is still present. Using correntropy [11], an extension of the idea of a covariance function, we create a time based functional which describes some potentially nonlinear desired mapping function. This form of a solution may provide a fruitful line of research for creating more efficient representations of functionals in a RKHS, while theoretically providing computational complexity in the test set similar to Wiener solution.

Adapting the Exploration Rate for Value-of-Information-Based Reinforcement Learning

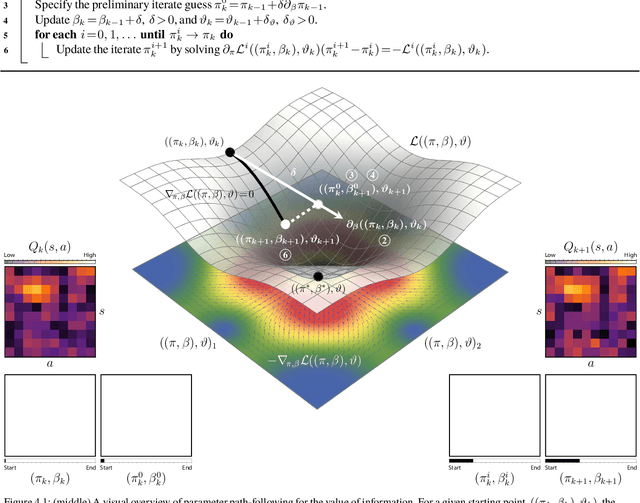
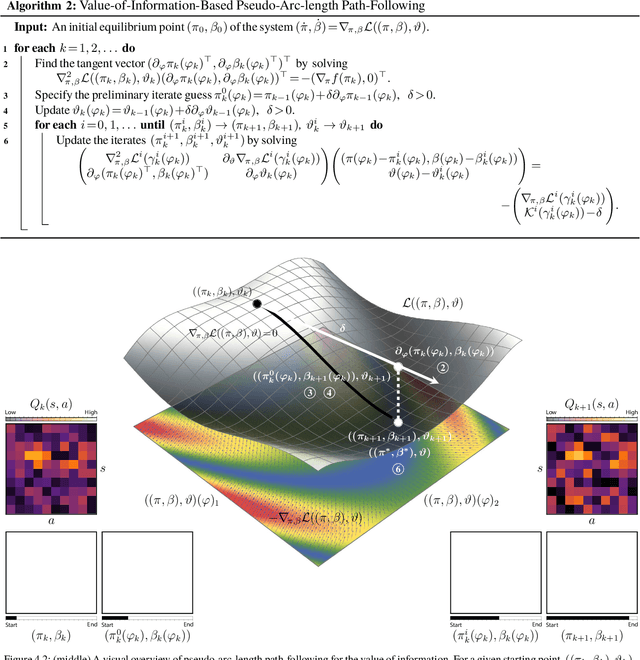
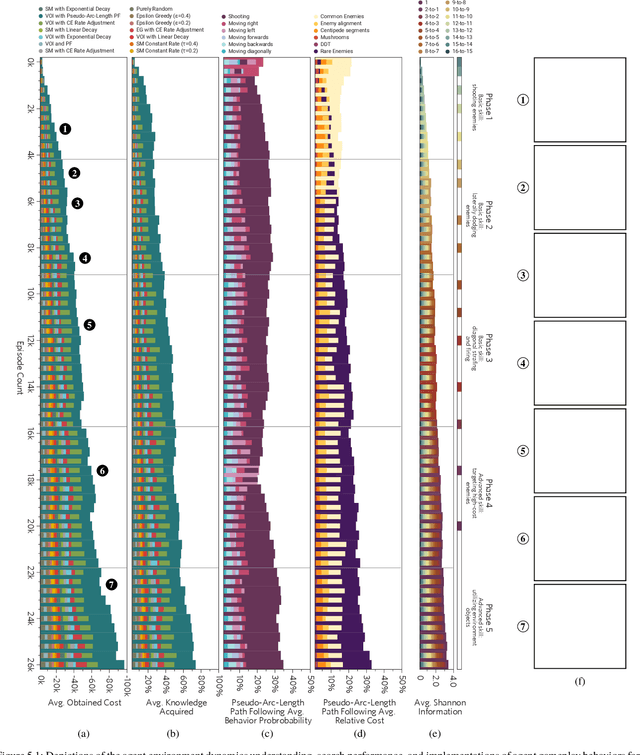
In this paper, we consider the problem of adjusting the exploration rate when using value-of-information-based exploration. We do this by converting the value-of-information optimization into a problem of finding equilibria of a flow for a changing exploration rate. We then develop an efficient path-following scheme for converging to these equilibria and hence uncovering optimal action-selection policies. Under this scheme, the exploration rate is automatically adapted according to the agent's experiences. Global convergence is theoretically assured. We first evaluate our exploration-rate adaptation on the Nintendo GameBoy games Centipede and Millipede. We demonstrate aspects of the search process, like that it yields a hierarchy of state abstractions. We also show that our approach returns better policies in fewer episodes than conventional search strategies relying on heuristic, annealing-based exploration-rate adjustments. We then illustrate that these trends hold for deep, value-of-information-based agents that learn to play ten simple games and over forty more complicated games for the Nintendo GameBoy system. Performance either near or well above the level of human play is observed.

The Functional Wiener Filter

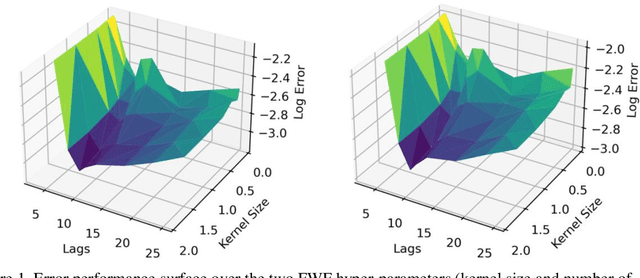
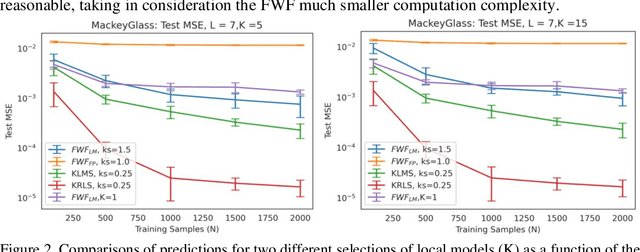
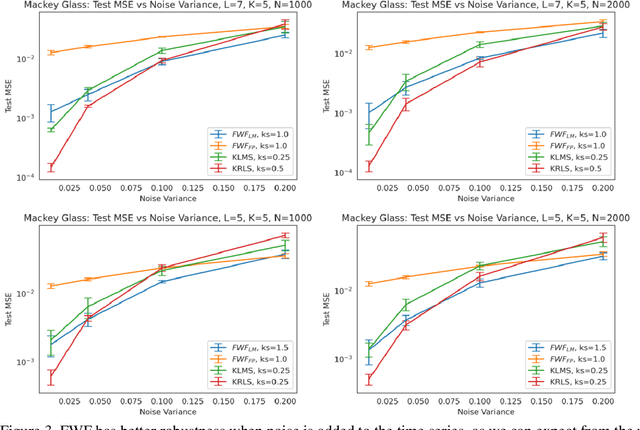
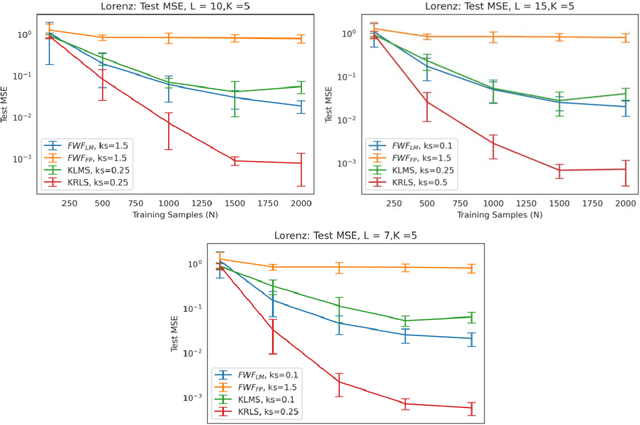
This paper presents a close form solution in Reproducing Kernel Hilbert Space (RKHS) for the famed Wiener filter, which we called the functional Wiener filter(FWF). Instead of using the Wiener-Hopf factorization theory, here we define a new lagged RKHS that embeds signal statistics based on the correntropy function. In essence, we extend Parzen$'$s work on the autocorrelation function RKHS to nonlinear functional spaces. The FWF derivation is also quite different from kernel adaptive filtering (KAF) algorithms, which utilize a search approach. The analytic FWF solution is derived in the Gaussian kernel RKHS with a constant computational complexity similar to the Wiener solution, and never composes nor employs the error as in conventional optimal modeling. Because of the lack of congruence between the Gaussian RKHS and the space of time series, we compare performance of two pre-imaging algorithms: a fixed-point optimization (FWFFP) that finds and approximate solution in the RKHS, and a local model implementation named FWFLM. The experimental results show that the FWF performance is on par with the KAF for time series modeling, and it requires far less computation.