An Analytic Solution for Kernel Adaptive Filtering

Conventional kernel adaptive filtering (KAF) uses a prescribed, positive definite, nonlinear function to define the Reproducing Kernel Hilbert Space (RKHS), where the optimal solution for mean square error estimation is approximated using search techniques. Instead, this paper proposes to embed the full statistics of the input data in the kernel definition, obtaining the first analytical solution for nonlinear regression and nonlinear adaptive filtering applications. We call this solution the Functional Wiener Filter (FWF). Conceptually, the methodology is an extension of Parzen's work on the autocorrelation RKHS to nonlinear functional spaces. We provide an extended functional Wiener equation, and present a solution to this equation in an explicit, finite dimensional, data-dependent RKHS. We further explain the necessary requirements to compute the analytical solution in RKHS, which is beyond traditional methodologies based on the kernel trick. The FWF analytic solution to the nonlinear minimum mean square error problem has better accuracy than other kernel-based algorithms in synthetic, stationary data. In real world time series, it has comparable accuracy to KAF but displays constant complexity with respect to number of training samples. For evaluation, it is as computationally efficient as the Wiener solution (with a larger number of dimensions than the linear case). We also show how the difference equation learned by the FWF from data can be extracted leading to system identification applications, which extend the possible applications of the FWF beyond optimal nonlinear filtering.

An Alternate View on Optimal Filtering in an RKHS

Kernel Adaptive Filtering (KAF) are mathematically principled methods which search for a function in a Reproducing Kernel Hilbert Space. While they work well for tasks such as time series prediction and system identification they are plagued by a linear relationship between number of training samples and model size, hampering their use on the very large data sets common in today's data saturated world. Previous methods try to solve this issue by sparsification. We describe a novel view of optimal filtering which may provide a route towards solutions in a RKHS which do not necessarily have this linear growth in model size. We do this by defining a RKHS in which the time structure of a stochastic process is still present. Using correntropy [11], an extension of the idea of a covariance function, we create a time based functional which describes some potentially nonlinear desired mapping function. This form of a solution may provide a fruitful line of research for creating more efficient representations of functionals in a RKHS, while theoretically providing computational complexity in the test set similar to Wiener solution.

The Functional Wiener Filter

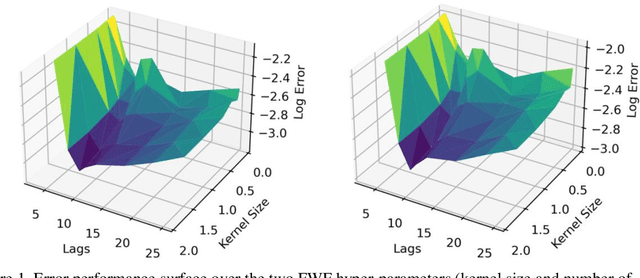
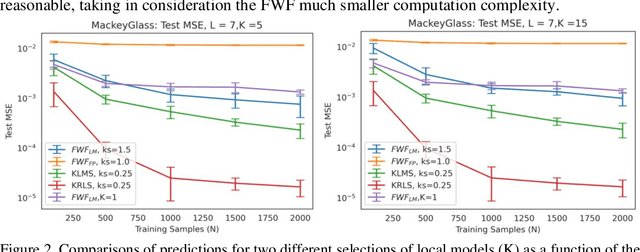
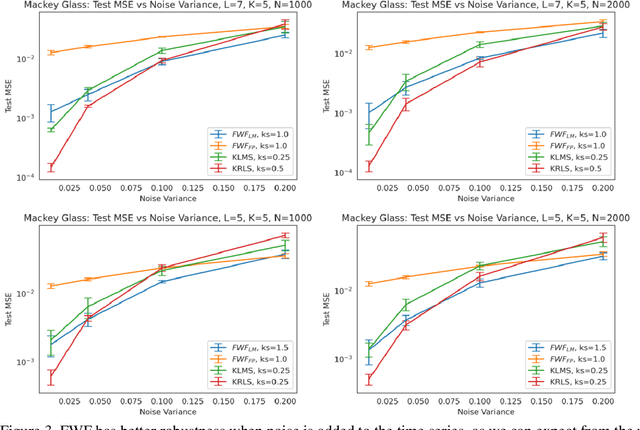
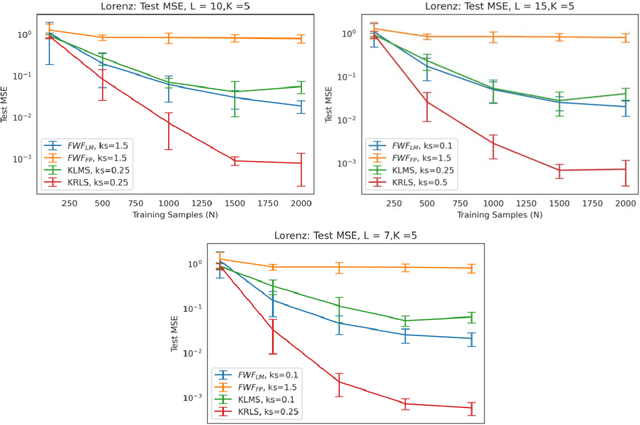
This paper presents a close form solution in Reproducing Kernel Hilbert Space (RKHS) for the famed Wiener filter, which we called the functional Wiener filter(FWF). Instead of using the Wiener-Hopf factorization theory, here we define a new lagged RKHS that embeds signal statistics based on the correntropy function. In essence, we extend Parzen$'$s work on the autocorrelation function RKHS to nonlinear functional spaces. The FWF derivation is also quite different from kernel adaptive filtering (KAF) algorithms, which utilize a search approach. The analytic FWF solution is derived in the Gaussian kernel RKHS with a constant computational complexity similar to the Wiener solution, and never composes nor employs the error as in conventional optimal modeling. Because of the lack of congruence between the Gaussian RKHS and the space of time series, we compare performance of two pre-imaging algorithms: a fixed-point optimization (FWFFP) that finds and approximate solution in the RKHS, and a local model implementation named FWFLM. The experimental results show that the FWF performance is on par with the KAF for time series modeling, and it requires far less computation.

A Stable Combinatorial Particle Swarm Optimization for Scalable Feature Selection in Gene Expression Data

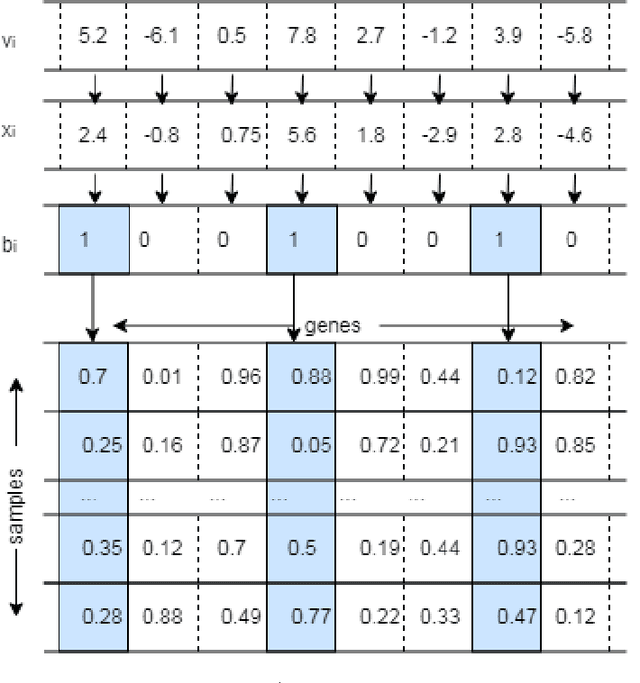
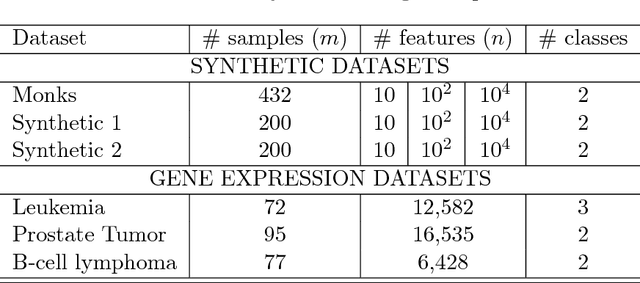
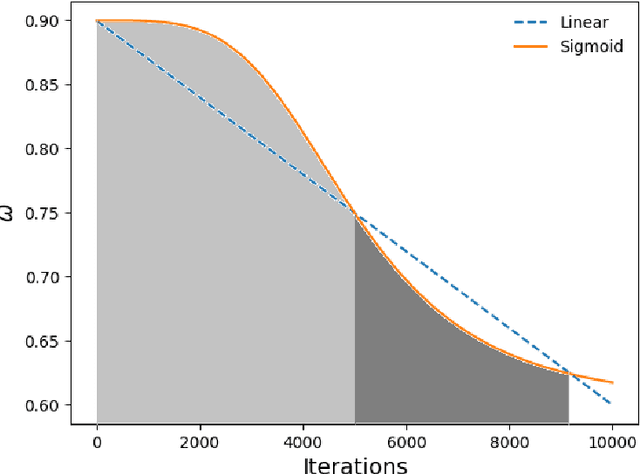
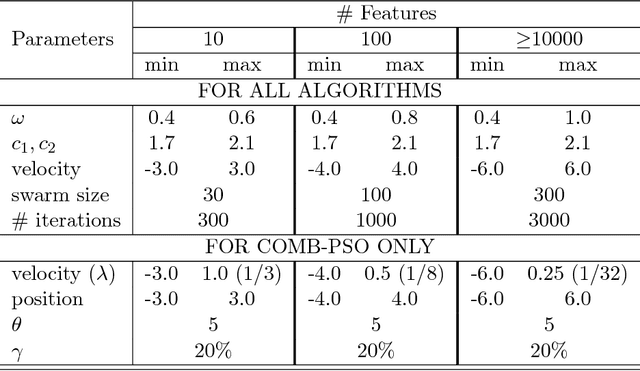
Evolutionary computation (EC) algorithms, such as discrete and multi-objective versions of particle swarm optimization (PSO), have been applied to solve the Feature selection (FS) problem, tackling the combinatorial explosion of search spaces that are peppered with local minima. Furthermore, high-dimensional FS problems such as finding a small set of biomarkers to make a diagnostic call add an additional challenge as such methods ability to pick out the most important features must remain unchanged in decision spaces of increasing dimensions and presence of irrelevant features. We developed a combinatorial PSO algorithm, called COMB-PSO, that scales up to high-dimensional gene expression data while still selecting the smallest subsets of genes that allow reliable classification of samples. In particular, COMB-PSO enhances the encoding, speed of convergence, control of divergence and diversity of the conventional PSO algorithm, balancing exploration and exploitation of the search space. Applying our approach on real gene expression data of different cancers, COMB-PSO finds gene sets of smallest size that allow a reliable classification of the underlying disease classes.

Measures of Entropy from Data Using Infinitely Divisible Kernels

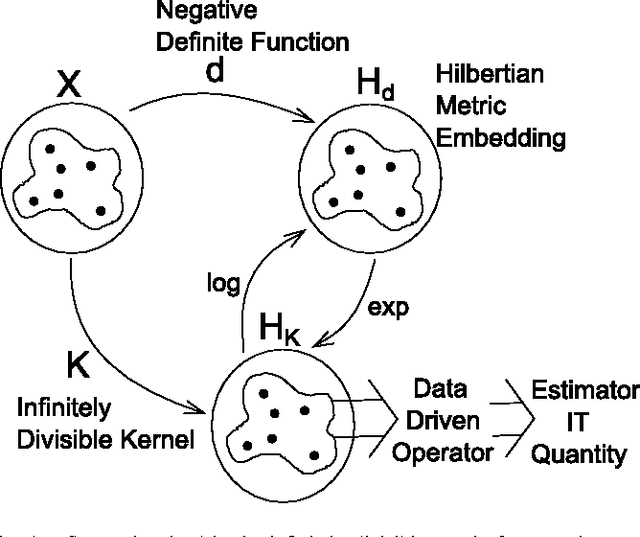
Information theory provides principled ways to analyze different inference and learning problems such as hypothesis testing, clustering, dimensionality reduction, classification, among others. However, the use of information theoretic quantities as test statistics, that is, as quantities obtained from empirical data, poses a challenging estimation problem that often leads to strong simplifications such as Gaussian models, or the use of plug in density estimators that are restricted to certain representation of the data. In this paper, a framework to non-parametrically obtain measures of entropy directly from data using operators in reproducing kernel Hilbert spaces defined by infinitely divisible kernels is presented. The entropy functionals, which bear resemblance with quantum entropies, are defined on positive definite matrices and satisfy similar axioms to those of Renyi's definition of entropy. Convergence of the proposed estimators follows from concentration results on the difference between the ordered spectrum of the Gram matrices and the integral operators associated to the population quantities. In this way, capitalizing on both the axiomatic definition of entropy and on the representation power of positive definite kernels, the proposed measure of entropy avoids the estimation of the probability distribution underlying the data. Moreover, estimators of kernel-based conditional entropy and mutual information are also defined. Numerical experiments on independence tests compare favourably with state of the art.

Rate-Distortion Auto-Encoders

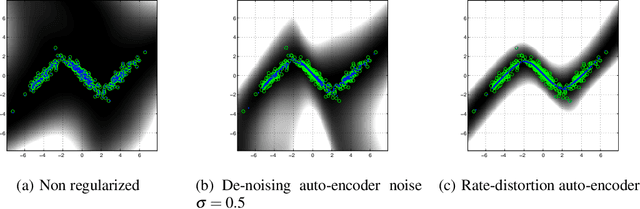
A rekindled the interest in auto-encoder algorithms has been spurred by recent work on deep learning. Current efforts have been directed towards effective training of auto-encoder architectures with a large number of coding units. Here, we propose a learning algorithm for auto-encoders based on a rate-distortion objective that minimizes the mutual information between the inputs and the outputs of the auto-encoder subject to a fidelity constraint. The goal is to learn a representation that is minimally committed to the input data, but that is rich enough to reconstruct the inputs up to certain level of distortion. Minimizing the mutual information acts as a regularization term whereas the fidelity constraint can be understood as a risk functional in the conventional statistical learning setting. The proposed algorithm uses a recently introduced measure of entropy based on infinitely divisible matrices that avoids the plug in estimation of densities. Experiments using over-complete bases show that the rate-distortion auto-encoders can learn a regularized input-output mapping in an implicit manner.

Information Theoretic Learning with Infinitely Divisible Kernels

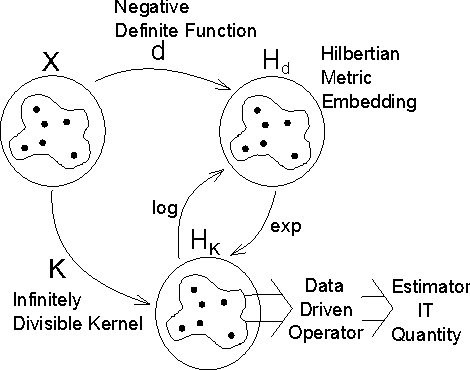
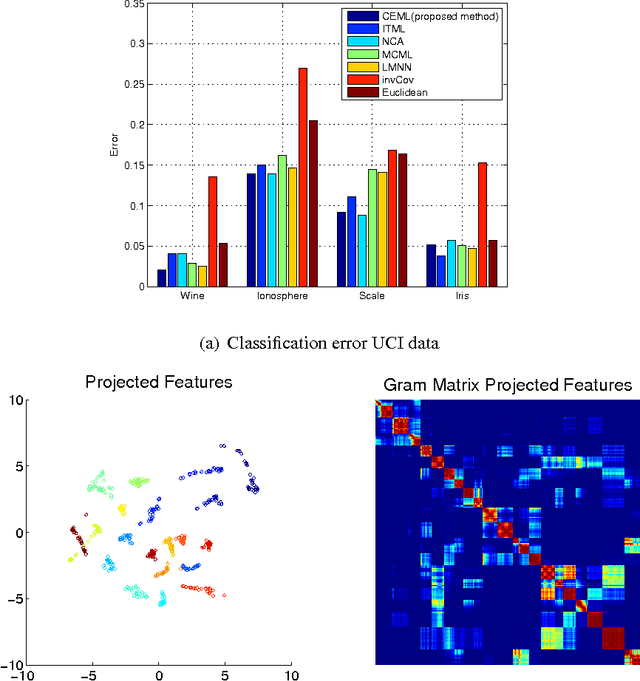
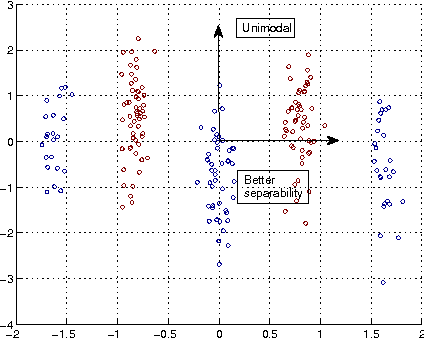
In this paper, we develop a framework for information theoretic learning based on infinitely divisible matrices. We formulate an entropy-like functional on positive definite matrices based on Renyi's axiomatic definition of entropy and examine some key properties of this functional that lead to the concept of infinite divisibility. The proposed formulation avoids the plug in estimation of density and brings along the representation power of reproducing kernel Hilbert spaces. As an application example, we derive a supervised metric learning algorithm using a matrix based analogue to conditional entropy achieving results comparable with the state of the art.