Benjamin Colburn
A Simple and Effective Method for Uncertainty Quantification and OOD Detection
Aug 01, 2025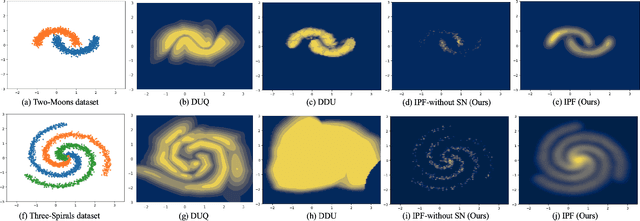
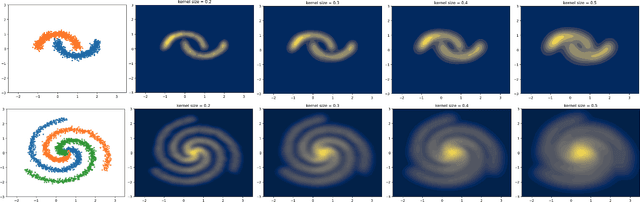
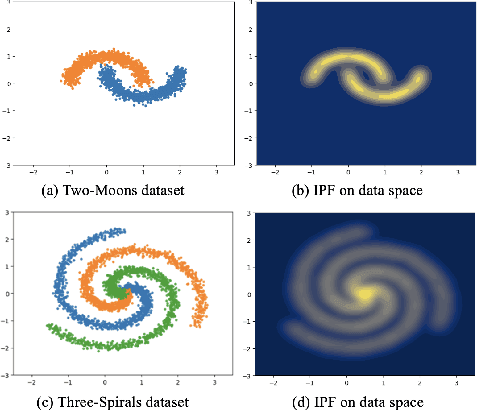
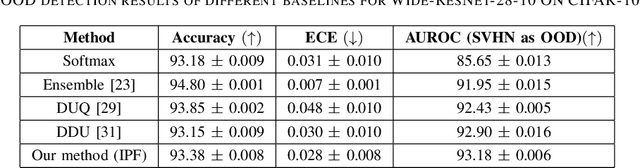
Abstract:Bayesian neural networks and deep ensemble methods have been proposed for uncertainty quantification; however, they are computationally intensive and require large storage. By utilizing a single deterministic model, we can solve the above issue. We propose an effective method based on feature space density to quantify uncertainty for distributional shifts and out-of-distribution (OOD) detection. Specifically, we leverage the information potential field derived from kernel density estimation to approximate the feature space density of the training set. By comparing this density with the feature space representation of test samples, we can effectively determine whether a distributional shift has occurred. Experiments were conducted on a 2D synthetic dataset (Two Moons and Three Spirals) as well as an OOD detection task (CIFAR-10 vs. SVHN). The results demonstrate that our method outperforms baseline models.
An Analytic Solution for Kernel Adaptive Filtering
Feb 05, 2024Abstract:Conventional kernel adaptive filtering (KAF) uses a prescribed, positive definite, nonlinear function to define the Reproducing Kernel Hilbert Space (RKHS), where the optimal solution for mean square error estimation is approximated using search techniques. Instead, this paper proposes to embed the full statistics of the input data in the kernel definition, obtaining the first analytical solution for nonlinear regression and nonlinear adaptive filtering applications. We call this solution the Functional Wiener Filter (FWF). Conceptually, the methodology is an extension of Parzen's work on the autocorrelation RKHS to nonlinear functional spaces. We provide an extended functional Wiener equation, and present a solution to this equation in an explicit, finite dimensional, data-dependent RKHS. We further explain the necessary requirements to compute the analytical solution in RKHS, which is beyond traditional methodologies based on the kernel trick. The FWF analytic solution to the nonlinear minimum mean square error problem has better accuracy than other kernel-based algorithms in synthetic, stationary data. In real world time series, it has comparable accuracy to KAF but displays constant complexity with respect to number of training samples. For evaluation, it is as computationally efficient as the Wiener solution (with a larger number of dimensions than the linear case). We also show how the difference equation learned by the FWF from data can be extracted leading to system identification applications, which extend the possible applications of the FWF beyond optimal nonlinear filtering.
An Alternate View on Optimal Filtering in an RKHS
Dec 19, 2023Abstract:Kernel Adaptive Filtering (KAF) are mathematically principled methods which search for a function in a Reproducing Kernel Hilbert Space. While they work well for tasks such as time series prediction and system identification they are plagued by a linear relationship between number of training samples and model size, hampering their use on the very large data sets common in today's data saturated world. Previous methods try to solve this issue by sparsification. We describe a novel view of optimal filtering which may provide a route towards solutions in a RKHS which do not necessarily have this linear growth in model size. We do this by defining a RKHS in which the time structure of a stochastic process is still present. Using correntropy [11], an extension of the idea of a covariance function, we create a time based functional which describes some potentially nonlinear desired mapping function. This form of a solution may provide a fruitful line of research for creating more efficient representations of functionals in a RKHS, while theoretically providing computational complexity in the test set similar to Wiener solution.
The Functional Wiener Filter
Dec 31, 2022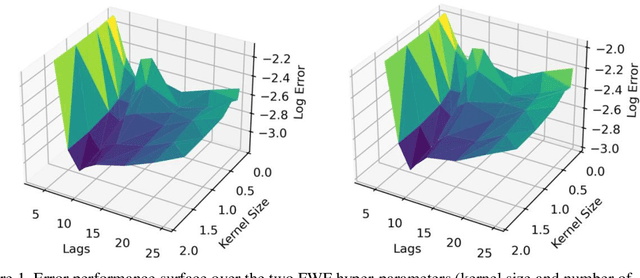
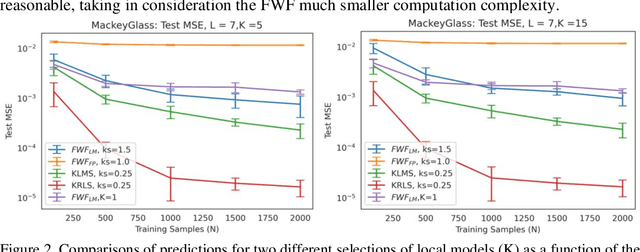
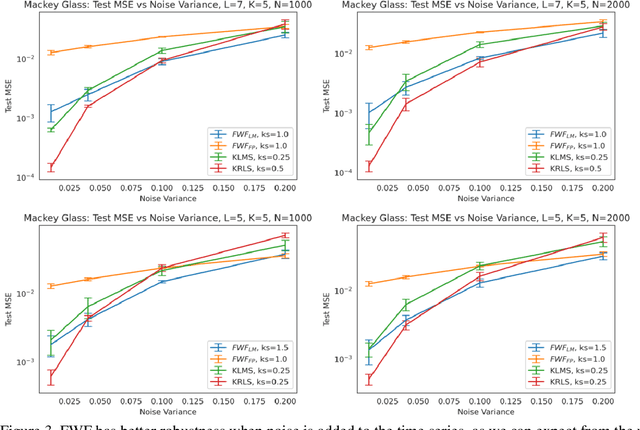
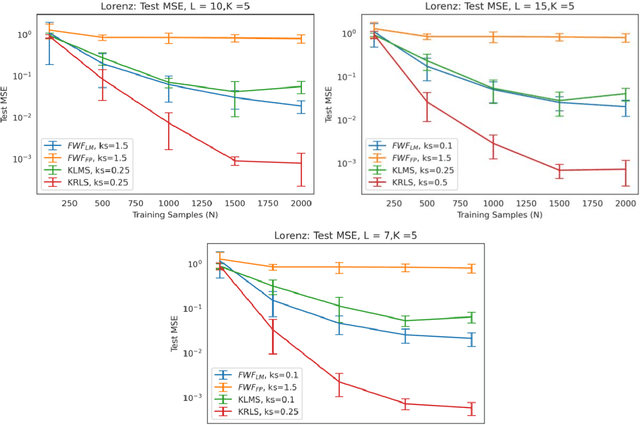
Abstract:This paper presents a close form solution in Reproducing Kernel Hilbert Space (RKHS) for the famed Wiener filter, which we called the functional Wiener filter(FWF). Instead of using the Wiener-Hopf factorization theory, here we define a new lagged RKHS that embeds signal statistics based on the correntropy function. In essence, we extend Parzen$'$s work on the autocorrelation function RKHS to nonlinear functional spaces. The FWF derivation is also quite different from kernel adaptive filtering (KAF) algorithms, which utilize a search approach. The analytic FWF solution is derived in the Gaussian kernel RKHS with a constant computational complexity similar to the Wiener solution, and never composes nor employs the error as in conventional optimal modeling. Because of the lack of congruence between the Gaussian RKHS and the space of time series, we compare performance of two pre-imaging algorithms: a fixed-point optimization (FWFFP) that finds and approximate solution in the RKHS, and a local model implementation named FWFLM. The experimental results show that the FWF performance is on par with the KAF for time series modeling, and it requires far less computation.
SignalTrain: Profiling Audio Compressors with Deep Neural Networks
May 30, 2019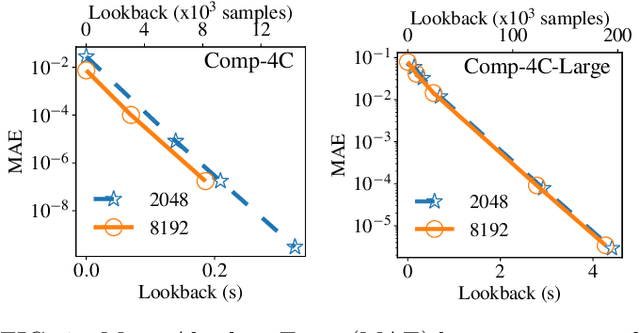
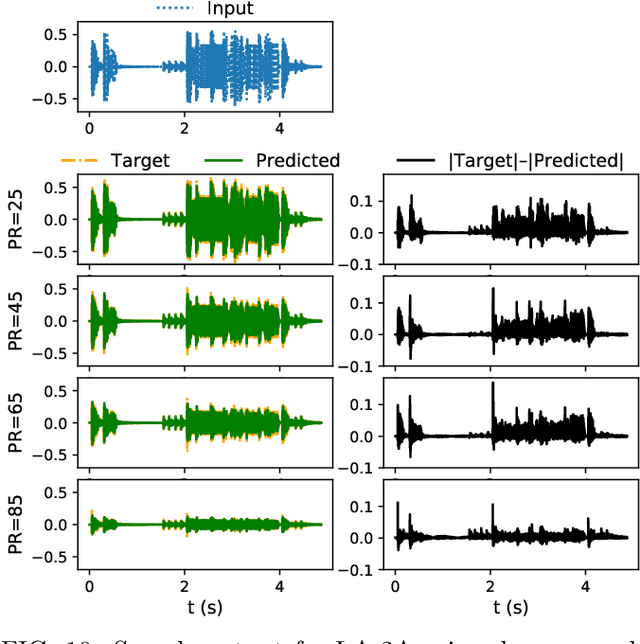
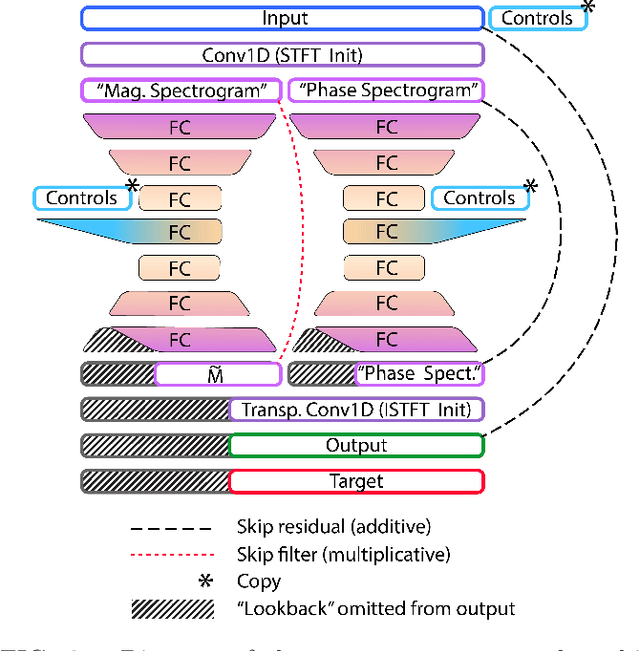
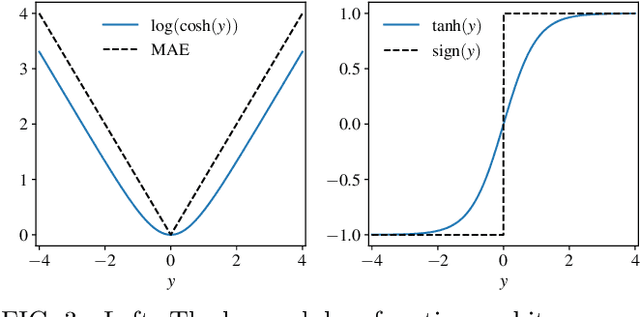
Abstract:In this work we present a data-driven approach for predicting the behavior of (i.e., profiling) a given non-linear audio signal processing effect (henceforth "audio effect"). Our objective is to learn a mapping function that maps the unprocessed audio to the processed by the audio effect to be profiled, using time-domain samples. To that aim, we employ a deep auto-encoder model that is conditioned on both time-domain samples and the control parameters of the target audio effect. As a test-case study, we focus on the offline profiling of two dynamic range compression audio effects, one software-based and the other analog. Compressors were chosen because they are a widely used and important set of effects and because their parameterized nonlinear time-dependent nature makes them a challenging problem for a system aiming to profile "general" audio effects. Results from our experimental procedure show that the primary functional and auditory characteristics of the compressors can be captured, however there is still sufficient audible noise to merit further investigation before such methods are applied to real-world audio processing workflows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge