The Functional Wiener Filter
Paper and Code
Dec 31, 2022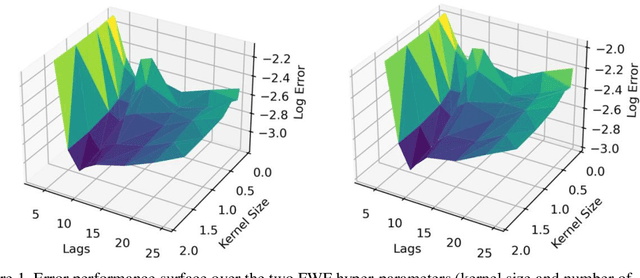
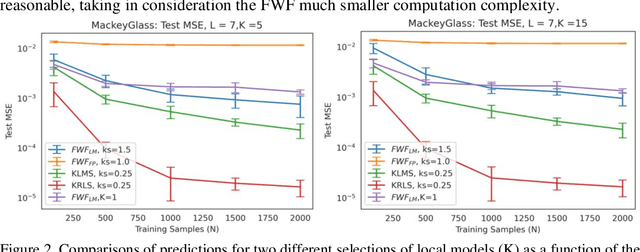
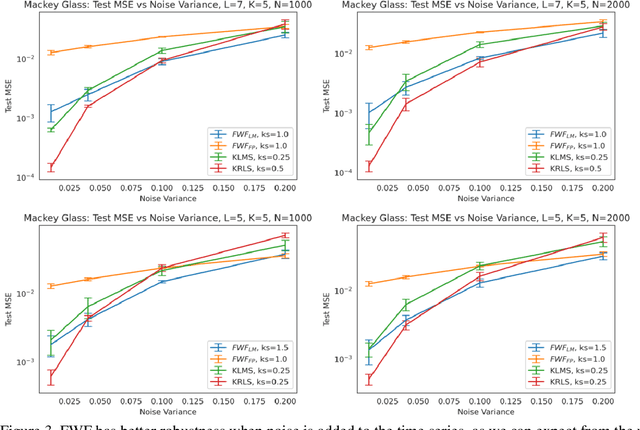
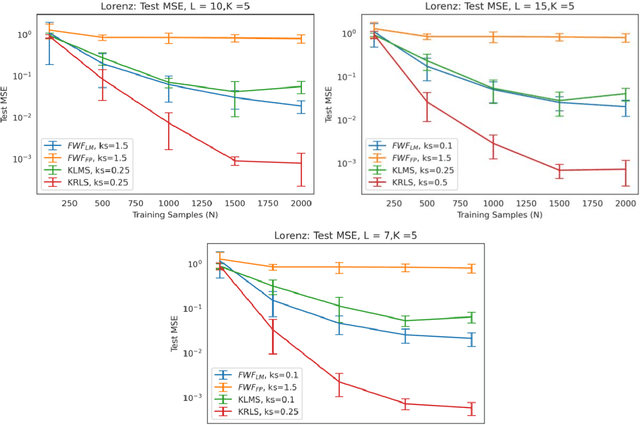
This paper presents a close form solution in Reproducing Kernel Hilbert Space (RKHS) for the famed Wiener filter, which we called the functional Wiener filter(FWF). Instead of using the Wiener-Hopf factorization theory, here we define a new lagged RKHS that embeds signal statistics based on the correntropy function. In essence, we extend Parzen$'$s work on the autocorrelation function RKHS to nonlinear functional spaces. The FWF derivation is also quite different from kernel adaptive filtering (KAF) algorithms, which utilize a search approach. The analytic FWF solution is derived in the Gaussian kernel RKHS with a constant computational complexity similar to the Wiener solution, and never composes nor employs the error as in conventional optimal modeling. Because of the lack of congruence between the Gaussian RKHS and the space of time series, we compare performance of two pre-imaging algorithms: a fixed-point optimization (FWFFP) that finds and approximate solution in the RKHS, and a local model implementation named FWFLM. The experimental results show that the FWF performance is on par with the KAF for time series modeling, and it requires far less computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge