Murali Rao
Measures of Entropy from Data Using Infinitely Divisible Kernels
Sep 01, 2014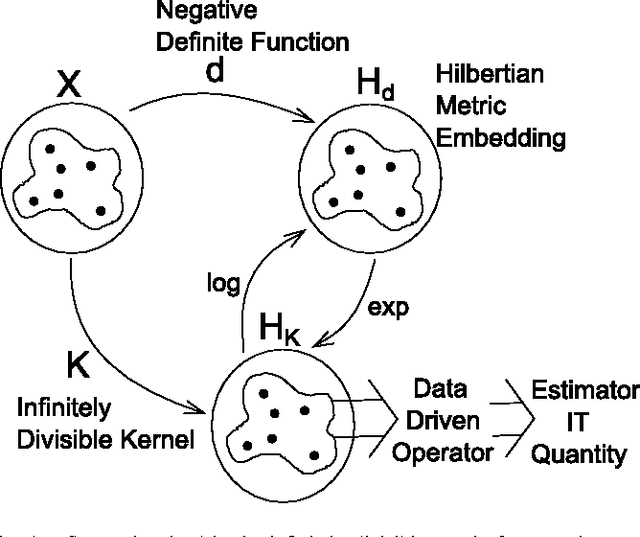


Abstract:Information theory provides principled ways to analyze different inference and learning problems such as hypothesis testing, clustering, dimensionality reduction, classification, among others. However, the use of information theoretic quantities as test statistics, that is, as quantities obtained from empirical data, poses a challenging estimation problem that often leads to strong simplifications such as Gaussian models, or the use of plug in density estimators that are restricted to certain representation of the data. In this paper, a framework to non-parametrically obtain measures of entropy directly from data using operators in reproducing kernel Hilbert spaces defined by infinitely divisible kernels is presented. The entropy functionals, which bear resemblance with quantum entropies, are defined on positive definite matrices and satisfy similar axioms to those of Renyi's definition of entropy. Convergence of the proposed estimators follows from concentration results on the difference between the ordered spectrum of the Gram matrices and the integral operators associated to the population quantities. In this way, capitalizing on both the axiomatic definition of entropy and on the representation power of positive definite kernels, the proposed measure of entropy avoids the estimation of the probability distribution underlying the data. Moreover, estimators of kernel-based conditional entropy and mutual information are also defined. Numerical experiments on independence tests compare favourably with state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge