Information Theoretic Learning with Infinitely Divisible Kernels
Paper and Code
Jun 04, 2013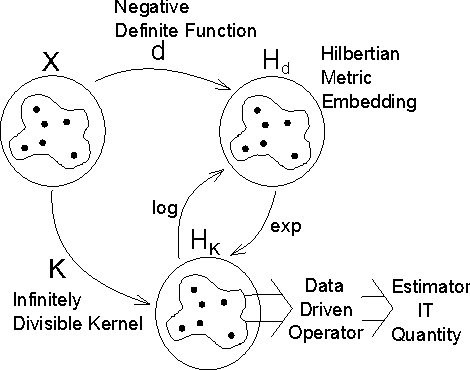
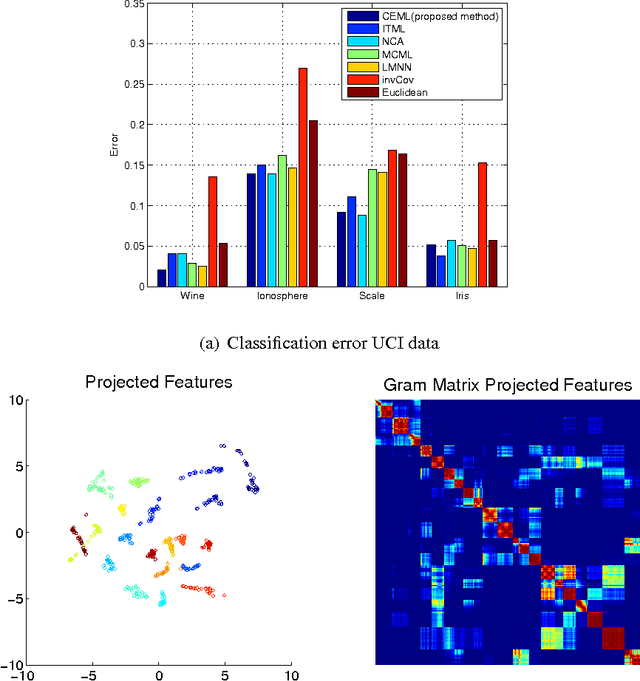
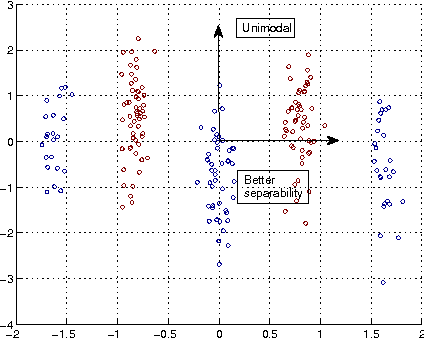
In this paper, we develop a framework for information theoretic learning based on infinitely divisible matrices. We formulate an entropy-like functional on positive definite matrices based on Renyi's axiomatic definition of entropy and examine some key properties of this functional that lead to the concept of infinite divisibility. The proposed formulation avoids the plug in estimation of density and brings along the representation power of reproducing kernel Hilbert spaces. As an application example, we derive a supervised metric learning algorithm using a matrix based analogue to conditional entropy achieving results comparable with the state of the art.
* Modified submission for International Conference on Learning
Representations 2013
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge