Generalized Correntropy for Robust Adaptive Filtering
Paper and Code
Apr 12, 2015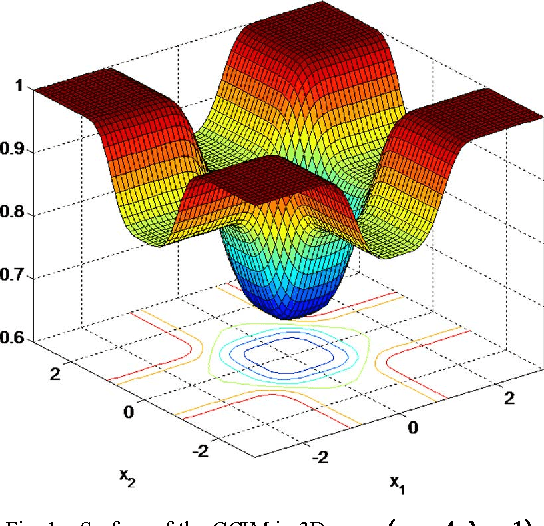
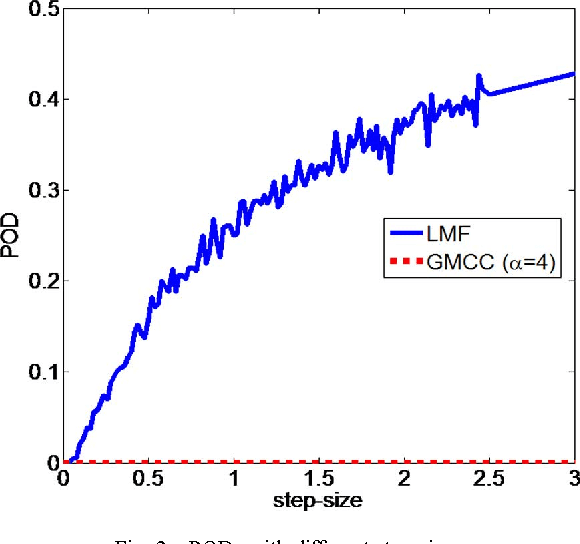
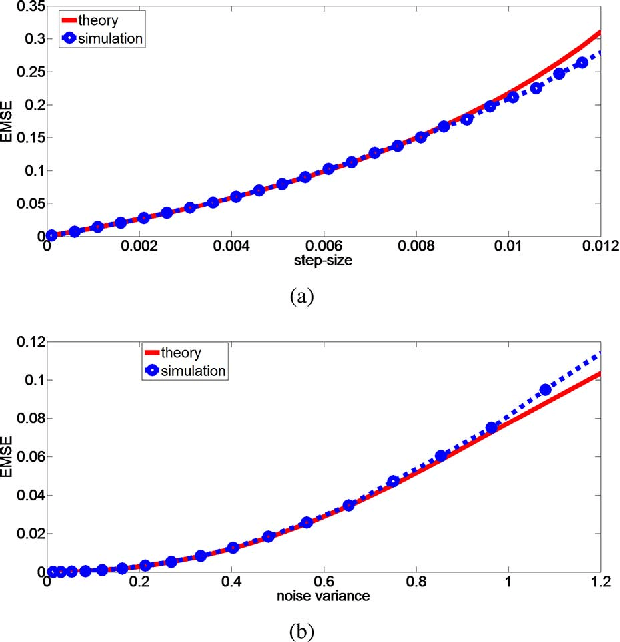
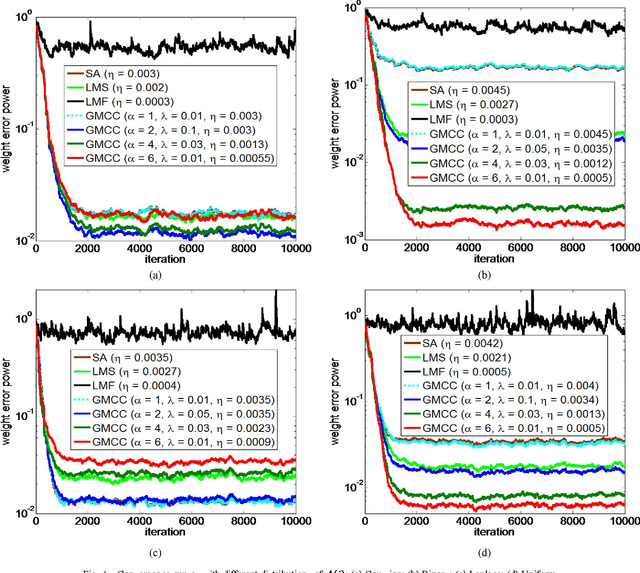
As a robust nonlinear similarity measure in kernel space, correntropy has received increasing attention in domains of machine learning and signal processing. In particular, the maximum correntropy criterion (MCC) has recently been successfully applied in robust regression and filtering. The default kernel function in correntropy is the Gaussian kernel, which is, of course, not always the best choice. In this work, we propose a generalized correntropy that adopts the generalized Gaussian density (GGD) function as the kernel (not necessarily a Mercer kernel), and present some important properties. We further propose the generalized maximum correntropy criterion (GMCC), and apply it to adaptive filtering. An adaptive algorithm, called the GMCC algorithm, is derived, and the mean square convergence performance is studied. We show that the proposed algorithm is very stable and can achieve zero probability of divergence (POD). Simulation results confirm the theoretical expectations and demonstrate the desirable performance of the new algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge