Graph state-space models

State-space models constitute an effective modeling tool to describe multivariate time series and operate by maintaining an updated representation of the system state from which predictions are made. Within this framework, relational inductive biases, e.g., associated with functional dependencies existing among signals, are not explicitly exploited leaving unattended great opportunities for effective modeling approaches. The manuscript aims, for the first time, at filling this gap by matching state-space modeling and spatio-temporal data where the relational information, say the functional graph capturing latent dependencies, is learned directly from data and is allowed to change over time. Within a probabilistic formulation that accounts for the uncertainty in the data-generating process, an encoder-decoder architecture is proposed to learn the state-space model end-to-end on a downstream task. The proposed methodological framework generalizes several state-of-the-art methods and demonstrates to be effective in extracting meaningful relational information while achieving optimal forecasting performance in controlled environments.

Transferring Chemical and Energetic Knowledge Between Molecular Systems with Machine Learning

Predicting structural and energetic properties of a molecular system is one of the fundamental tasks in molecular simulations, and it has use cases in chemistry, biology, and medicine. In the past decade, the advent of machine learning algorithms has impacted on molecular simulations for various tasks, including property prediction of atomistic systems. In this paper, we propose a novel methodology for transferring knowledge obtained from simple molecular systems to a more complex one, possessing a significantly larger number of atoms and degrees of freedom. In particular, we focus on the classification of high and low free-energy states. Our approach relies on utilizing (i) a novel hypergraph representation of molecules, encoding all relevant information for characterizing the potential energy of a conformation, and (ii) novel message passing and pooling layers for processing and making predictions on such hypergraph-structured data. Despite the complexity of the problem, our results show a remarkable AUC of 0.92 for transfer learning from tri-alanine to the deca-alanine system. Moreover, we show that the very same transfer learning approach can be used to group, in an unsupervised way, various secondary structures of deca-alanine in clusters having similar free-energy values. Our study represents a proof of concept that reliable transfer learning models for molecular systems can be designed paving the way to unexplored routes in prediction of structural and energetic properties of biologically relevant systems.

Message Passing Neural Networks for Hypergraphs

Hypergraph representations are both more efficient and better suited to describe data characterized by relations between two or more objects. In this work, we present a new graph neural network based on message passing capable of processing hypergraph-structured data. We show that the proposed model defines a design space for neural network models for hypergraphs, thus generalizing existing models for hypergraphs. We report experiments on a benchmark dataset for node classification, highlighting the effectiveness of the proposed model with respect to other state-of-the-art methods for graphs and hypergraphs. We also discuss the benefits of using hypergraph representations and, at the same time, highlight the limitation of using equivalent graph representations when the underlying problem has relations among more than two objects.

Learning Graph Cellular Automata

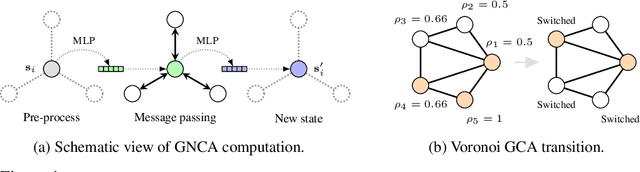
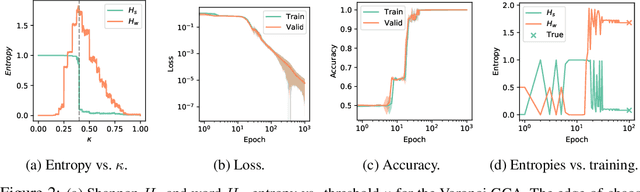
Cellular automata (CA) are a class of computational models that exhibit rich dynamics emerging from the local interaction of cells arranged in a regular lattice. In this work we focus on a generalised version of typical CA, called graph cellular automata (GCA), in which the lattice structure is replaced by an arbitrary graph. In particular, we extend previous work that used convolutional neural networks to learn the transition rule of conventional CA and we use graph neural networks to learn a variety of transition rules for GCA. First, we present a general-purpose architecture for learning GCA, and we show that it can represent any arbitrary GCA with finite and discrete state space. Then, we test our approach on three different tasks: 1) learning the transition rule of a GCA on a Voronoi tessellation; 2) imitating the behaviour of a group of flocking agents; 3) learning a rule that converges to a desired target state.

Learn to Synchronize, Synchronize to Learn

In recent years, the machine learning community has seen a continuous growing interest in research aimed at investigating dynamical aspects of both training procedures and perfected models. Of particular interest among recurrent neural networks, we have the Reservoir Computing (RC) paradigm for its conceptual simplicity and fast training scheme. Yet, the guiding principles under which RC operates are only partially understood. In this work, we study the properties behind learning dynamical systems with RC and propose a new guiding principle based on Generalized Synchronization (GS) granting its feasibility. We show that the well-known Echo State Property (ESP) implies and is implied by GS, so that theoretical results derived from the ESP still hold when GS does. However, by using GS one can profitably study the RC learning procedure by linking the reservoir dynamics with the readout training. Notably, this allows us to shed light on the interplay between the input encoding performed by the reservoir and the output produced by the readout optimized for the task at hand. In addition, we show that - as opposed to the ESP - satisfaction of the GS can be measured by means of the Mutual False Nearest Neighbors index, which makes effective to practitioners theoretical derivations.

Input representation in recurrent neural networks dynamics

Reservoir computing is a popular approach to design recurrent neural networks, due to its training simplicity and its approximation performance. The recurrent part of these networks is not trained (e.g. via gradient descent), making them appealing for analytical studies, raising the interest of a vast community of researcher spanning from dynamical systems to neuroscience. It emerges that, even in the simple linear case, the working principle of these networks is not fully understood and the applied research is usually driven by heuristics. A novel analysis of the dynamics of such networks is proposed, which allows one to express the state evolution using the controllability matrix. Such a matrix encodes salient characteristics of the network dynamics: in particular, its rank can be used as an input-indepedent measure of the memory of the network. Using the proposed approach, it is possible to compare different architectures and explain why a cyclic topology achieves favourable results.

Hierarchical Representation Learning in Graph Neural Networks with Node Decimation Pooling

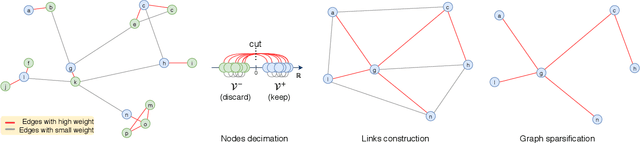
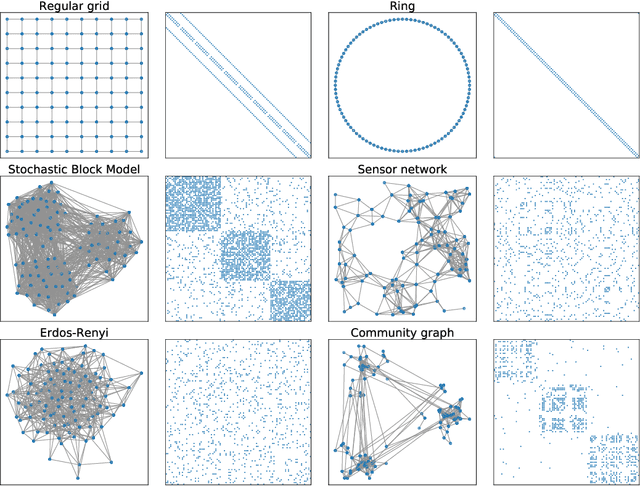
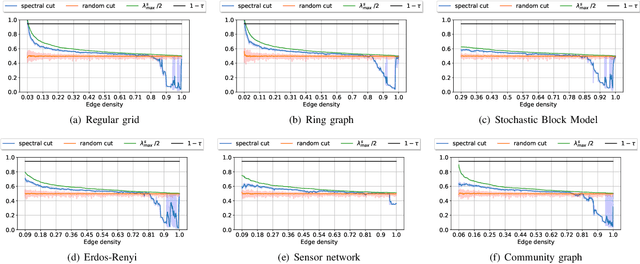
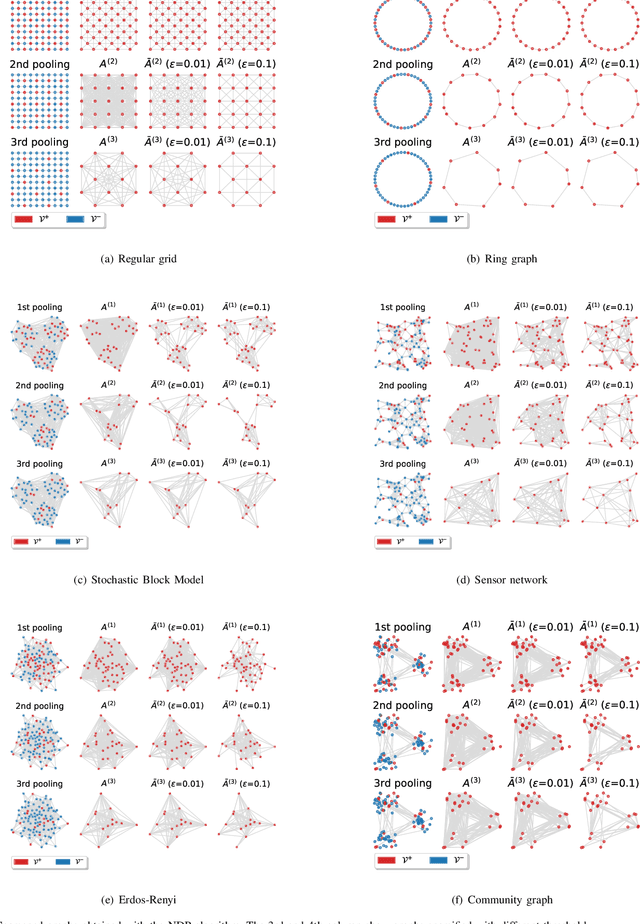
In graph neural networks (GNNs), pooling operators compute local summaries of input graphs to capture their global properties; in turn, they are fundamental operators for building deep GNNs that learn effective, hierarchical representations. In this work, we propose the Node Decimation Pooling (NDP), a pooling operator for GNNs that generates coarsened versions of a graph by leveraging on its topology only. During training, the GNN learns new representations for the vertices and fits them to a pyramid of coarsened graphs, which is computed in a pre-processing step. As theoretical contributions, we first demonstrate the equivalence between the MAXCUT partition and the node decimation procedure on which NDP is based. Then, we propose a procedure to sparsify the coarsened graphs for reducing the computational complexity in the GNN; we also demonstrate that it is possible to drop many edges without significantly altering the graph spectra of coarsened graphs. Experimental results show that NDP grants a significantly lower computational cost once compared to state-of-the-art graph pooling operators, while reaching, at the same time, competitive accuracy performance on a variety of graph classification tasks.

Distance-Preserving Graph Embeddings from Random Neural Features

We present Graph Random Neural Features (GRNF), a novel embedding method from graph-structured data to real vectors based on a family of graph neural networks. The embedding naturally deals with graph isomorphism and preserves, in probability, the metric structure of graph domain. In addition to being an explicit embedding method, it also allows to efficiently and effectively approximate graph metric distances (as well as complete kernel functions); a criterion to select the embedding dimension trading off the approximation accuracy with the computational cost is also provided. Derived GRNF can be used within traditional processing methods or as input layer of a larger graph neural network. The theoretical guarantees that accompany GRNF ensure that the considered graph distance is metric, hence allowing to distinguish any pair of non-isomorphic graphs.

Echo State Networks with Self-Normalizing Activations on the Hyper-Sphere

Among the various architectures of Recurrent Neural Networks, Echo State Networks (ESNs) emerged due to their simplified and inexpensive training procedure. These networks are known to be sensitive to the setting of hyper-parameters, which critically affect their behaviour. Results show that their performance is usually maximized in a narrow region of hyper-parameter space called edge of chaos. Finding such a region requires searching in hyper-parameter space in a sensible way: hyper-parameter configurations marginally outside such a region might yield networks exhibiting fully developed chaos, hence producing unreliable computations. The performance gain due to optimizing hyper-parameters can be studied by considering the memory--nonlinearity trade-off, i.e., the fact that increasing the nonlinear behavior of the network degrades its ability to remember past inputs, and vice-versa. In this paper, we propose a model of ESNs that eliminates critical dependence on hyper-parameters, resulting in networks that provably cannot enter a chaotic regime and, at the same time, denotes nonlinear behaviour in phase space characterised by a large memory of past inputs, comparable to the one of linear networks. Our contribution is supported by experiments corroborating our theoretical findings, showing that the proposed model displays dynamics that are rich-enough to approximate many common nonlinear systems used for benchmarking.

Autoregressive Models for Sequences of Graphs

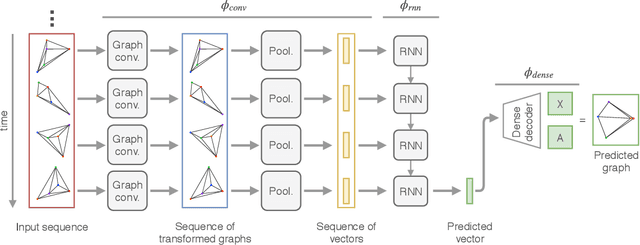
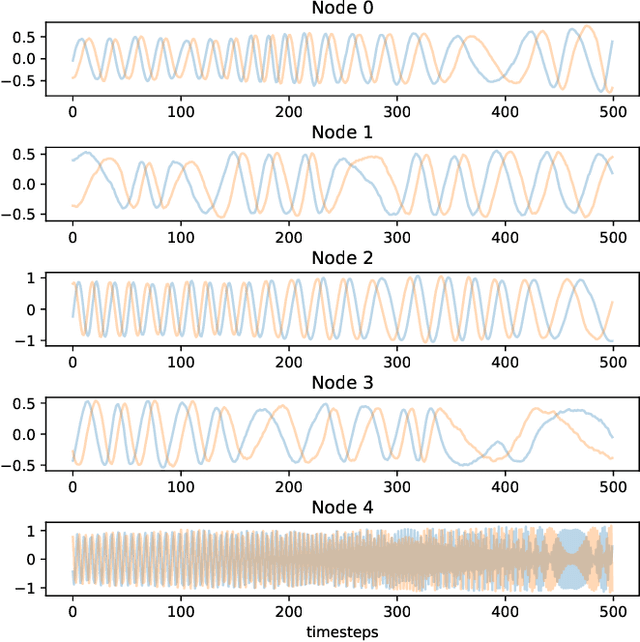
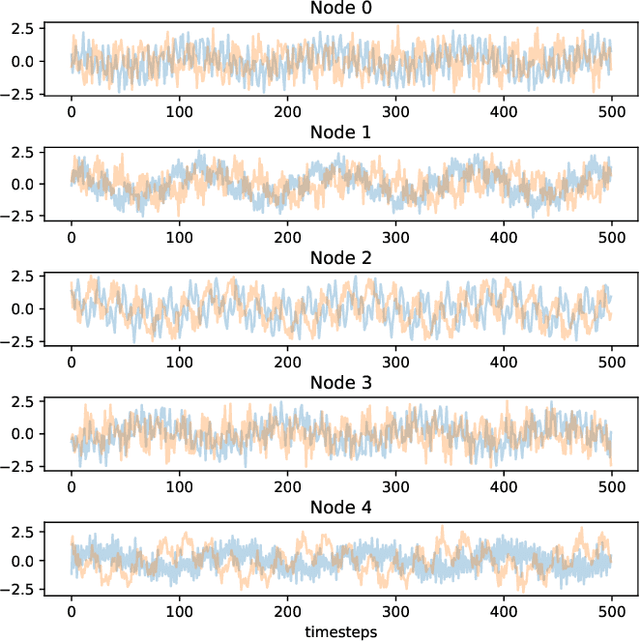
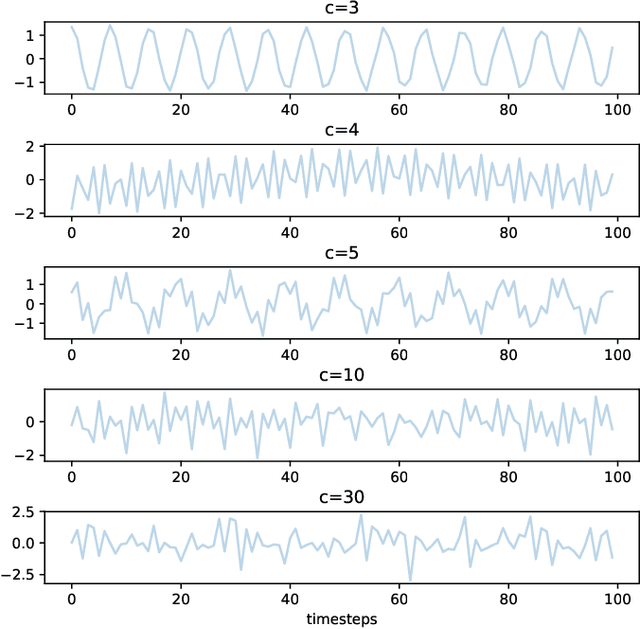
This paper proposes an autoregressive (AR) model for sequences of graphs, which generalises traditional AR models. A first novelty consists in formalising the AR model for a very general family of graphs, characterised by a variable topology, and attributes associated with nodes and edges. A graph neural network (GNN) is also proposed to learn the AR function associated with the graph-generating process (GGP), and subsequently predict the next graph in a sequence. The proposed method is compared with four baselines on synthetic GGPs, denoting a significantly better performance on all considered problems.