E(n)-equivariant Graph Neural Cellular Automata

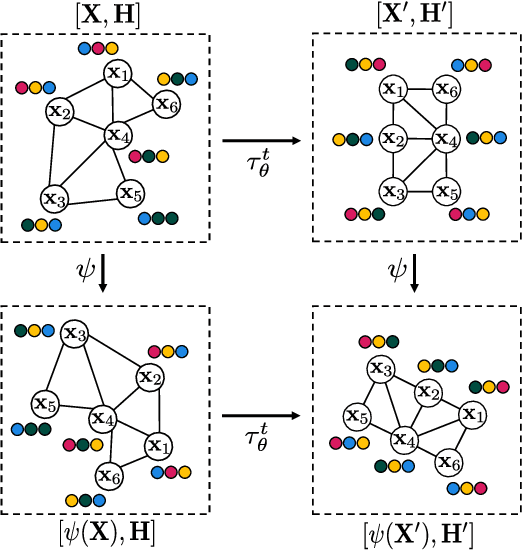
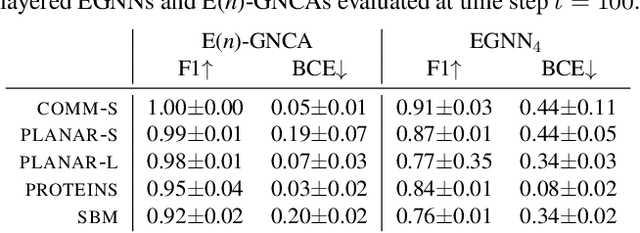
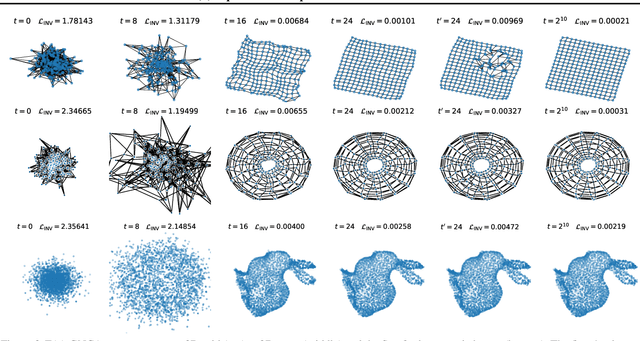
Cellular automata (CAs) are computational models exhibiting rich dynamics emerging from the local interaction of cells arranged in a regular lattice. Graph CAs (GCAs) generalise standard CAs by allowing for arbitrary graphs rather than regular lattices, similar to how Graph Neural Networks (GNNs) generalise Convolutional NNs. Recently, Graph Neural CAs (GNCAs) have been proposed as models built on top of standard GNNs that can be trained to approximate the transition rule of any arbitrary GCA. Existing GNCAs are anisotropic in the sense that their transition rules are not equivariant to translation, rotation, and reflection of the nodes' spatial locations. However, it is desirable for instances related by such transformations to be treated identically by the model. By replacing standard graph convolutions with E(n)-equivariant ones, we avoid anisotropy by design and propose a class of isotropic automata that we call E(n)-GNCAs. These models are lightweight, but can nevertheless handle large graphs, capture complex dynamics and exhibit emergent self-organising behaviours. We showcase the broad and successful applicability of E(n)-GNCAs on three different tasks: (i) pattern formation, (ii) graph auto-encoding, and (iii) simulation of E(n)-equivariant dynamical systems.

Generalised Implicit Neural Representations

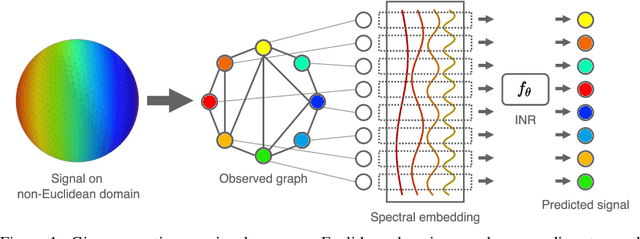
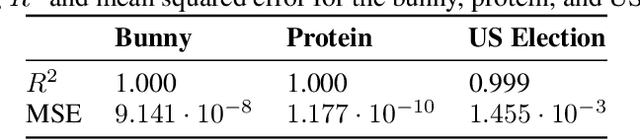
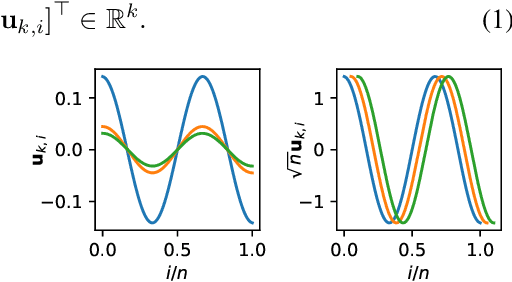
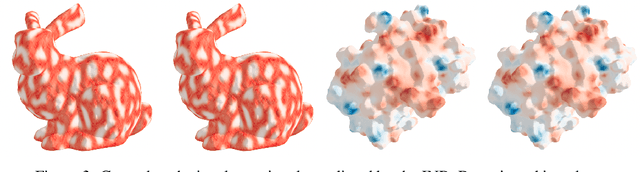
We consider the problem of learning implicit neural representations (INRs) for signals on non-Euclidean domains. In the Euclidean case, INRs are trained on a discrete sampling of a signal over a regular lattice. Here, we assume that the continuous signal exists on some unknown topological space from which we sample a discrete graph. In the absence of a coordinate system to identify the sampled nodes, we propose approximating their location with a spectral embedding of the graph. This allows us to train INRs without knowing the underlying continuous domain, which is the case for most graph signals in nature, while also making the INRs equivariant under the symmetry group of the domain. We show experiments with our method on various real-world signals on non-Euclidean domains.

Unsupervised Heterophilous Network Embedding via r-Ego Network Discrimination

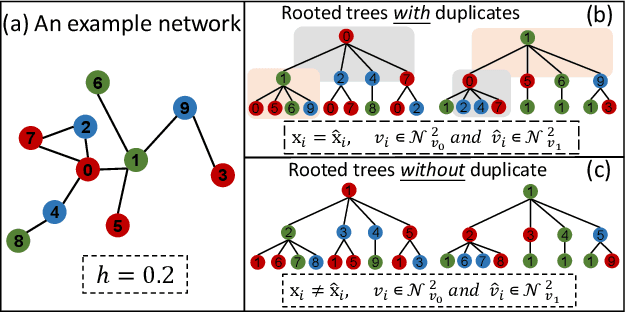
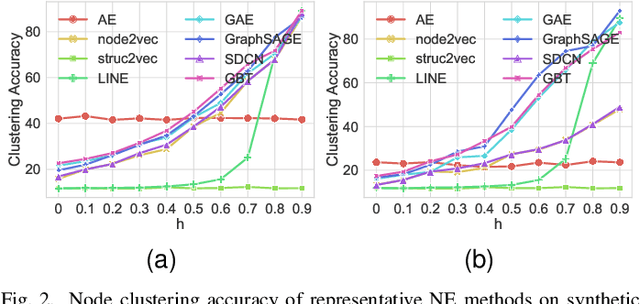
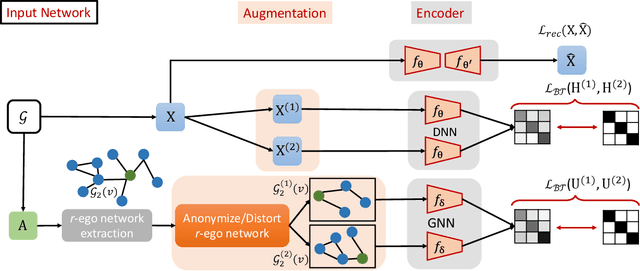
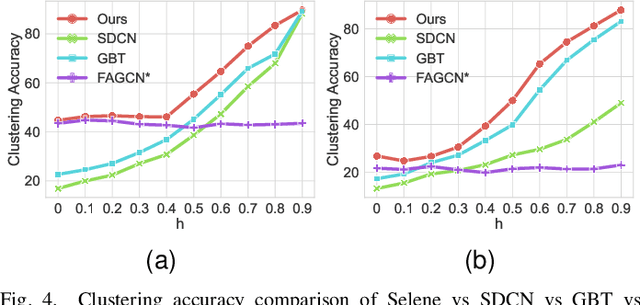
Recently, supervised network embedding (NE) has emerged as a predominant technique for representing complex systems that take the form of networks, and various downstream node- and network-level tasks have benefited from its remarkable developments. However, unsupervised NE still remains challenging due to the uncertainty in defining a learning objective. In addition, it is still an unexplored research question whether existing NE methods adapt well to heterophilous networks. This paper introduces the first empirical study on the influence of homophily ratio on the performance of existing unsupervised NE methods and reveals their limitations. Inspired by our empirical findings, we design unsupervised NE task as an r-ego network discrimination problem and further develop a SELf-supErvised Network Embedding (Selene) framework for learning useful node representations for both homophilous and heterophilous networks. Specifically, we propose a dual-channel feature embedding mechanism to fuse node attributes and network structure information and leverage a sampling and anonymisation strategy to break the implicit homophily assumption of existing embedding mechanisms. Lastly, we introduce a negative-sample-free SSL objective function to optimise the framework. We conduct extensive experiments and a series of ablation studies on 12 real-world datasets and 20 synthetic networks. Results demonstrate Selene's superior performance and confirm the effectiveness of each component.

Learning Graph Cellular Automata

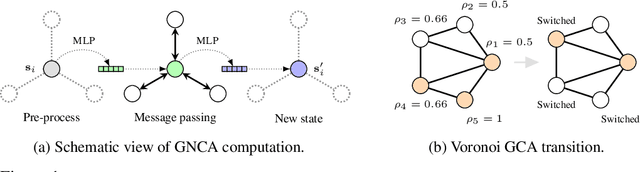
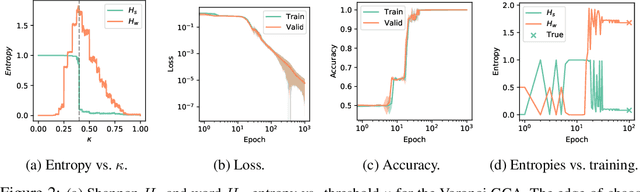
Cellular automata (CA) are a class of computational models that exhibit rich dynamics emerging from the local interaction of cells arranged in a regular lattice. In this work we focus on a generalised version of typical CA, called graph cellular automata (GCA), in which the lattice structure is replaced by an arbitrary graph. In particular, we extend previous work that used convolutional neural networks to learn the transition rule of conventional CA and we use graph neural networks to learn a variety of transition rules for GCA. First, we present a general-purpose architecture for learning GCA, and we show that it can represent any arbitrary GCA with finite and discrete state space. Then, we test our approach on three different tasks: 1) learning the transition rule of a GCA on a Voronoi tessellation; 2) imitating the behaviour of a group of flocking agents; 3) learning a rule that converges to a desired target state.

Understanding Pooling in Graph Neural Networks

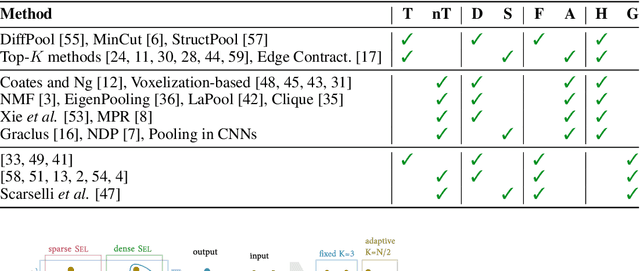
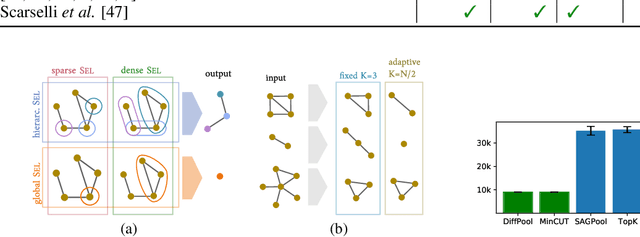
Inspired by the conventional pooling layers in convolutional neural networks, many recent works in the field of graph machine learning have introduced pooling operators to reduce the size of graphs. The great variety in the literature stems from the many possible strategies for coarsening a graph, which may depend on different assumptions on the graph structure or the specific downstream task. In this paper we propose a formal characterization of graph pooling based on three main operations, called selection, reduction, and connection, with the goal of unifying the literature under a common framework. Following this formalization, we introduce a taxonomy of pooling operators and categorize more than thirty pooling methods proposed in recent literature. We propose criteria to evaluate the performance of a pooling operator and use them to investigate and contrast the behavior of different classes of the taxonomy on a variety of tasks.

Graph Neural Networks in TensorFlow and Keras with Spektral

In this paper we present Spektral, an open-source Python library for building graph neural networks with TensorFlow and the Keras application programming interface. Spektral implements a large set of methods for deep learning on graphs, including message-passing and pooling operators, as well as utilities for processing graphs and loading popular benchmark datasets. The purpose of this library is to provide the essential building blocks for creating graph neural networks, focusing on the guiding principles of user-friendliness and quick prototyping on which Keras is based. Spektral is, therefore, suitable for absolute beginners and expert deep learning practitioners alike. In this work, we present an overview of Spektral's features and report the performance of the methods implemented by the library in scenarios of node classification, graph classification, and graph regression.

Hierarchical Representation Learning in Graph Neural Networks with Node Decimation Pooling

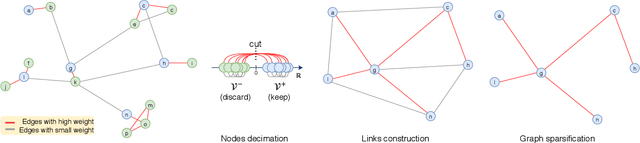
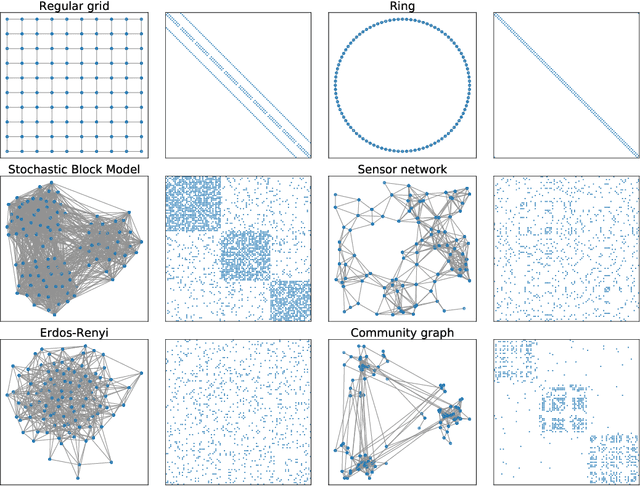
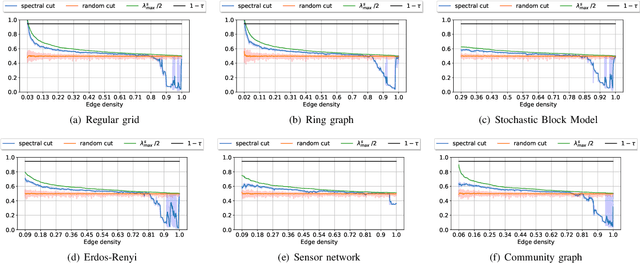
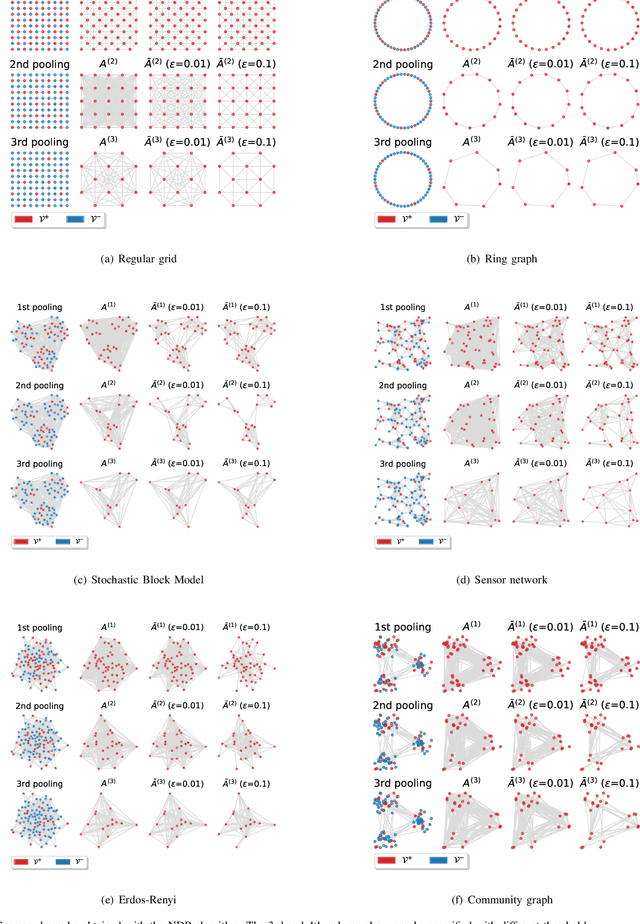
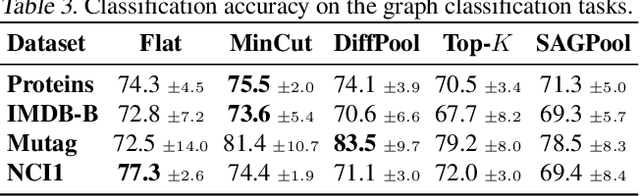
In graph neural networks (GNNs), pooling operators compute local summaries of input graphs to capture their global properties; in turn, they are fundamental operators for building deep GNNs that learn effective, hierarchical representations. In this work, we propose the Node Decimation Pooling (NDP), a pooling operator for GNNs that generates coarsened versions of a graph by leveraging on its topology only. During training, the GNN learns new representations for the vertices and fits them to a pyramid of coarsened graphs, which is computed in a pre-processing step. As theoretical contributions, we first demonstrate the equivalence between the MAXCUT partition and the node decimation procedure on which NDP is based. Then, we propose a procedure to sparsify the coarsened graphs for reducing the computational complexity in the GNN; we also demonstrate that it is possible to drop many edges without significantly altering the graph spectra of coarsened graphs. Experimental results show that NDP grants a significantly lower computational cost once compared to state-of-the-art graph pooling operators, while reaching, at the same time, competitive accuracy performance on a variety of graph classification tasks.

Mincut pooling in Graph Neural Networks

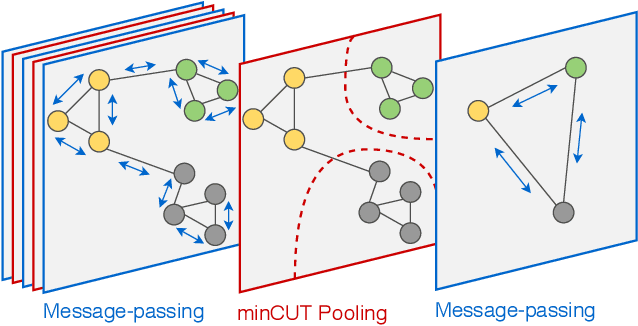
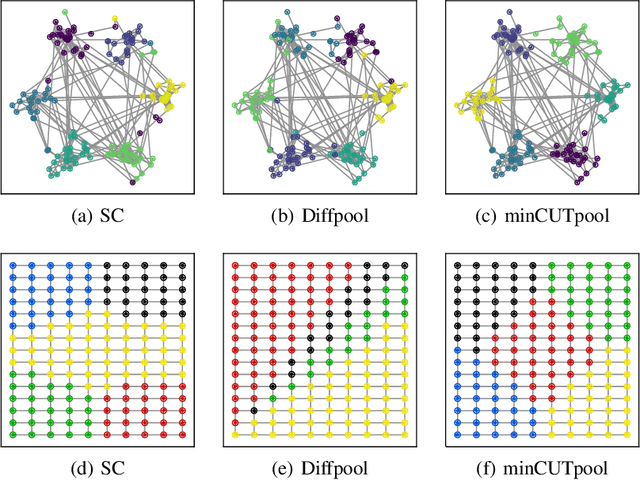
The advance of node pooling operations in Graph Neural Networks (GNNs) has lagged behind the feverish design of new message-passing techniques, and pooling remains an important and challenging endeavor for the design of deep architectures. In this paper, we propose a pooling operation for GNNs that leverages a differentiable unsupervised loss based on the mincut optimization objective. For each node, our method learns a soft cluster assignment vector that depends on the node features, the target inference task (e.g., graph classification), and, thanks to the mincut objective, also on the graph connectivity. Graph pooling is obtained by applying the matrix of assignment vectors to the adjacency matrix and the node features. We validate the effectiveness of the proposed pooling method on a variety of supervised and unsupervised tasks.

Autoregressive Models for Sequences of Graphs

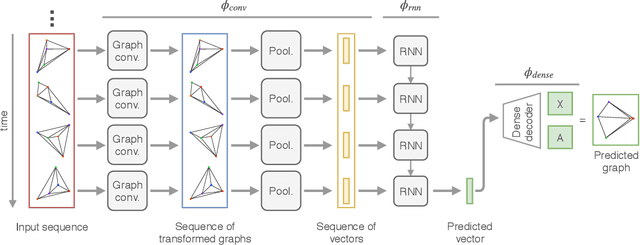
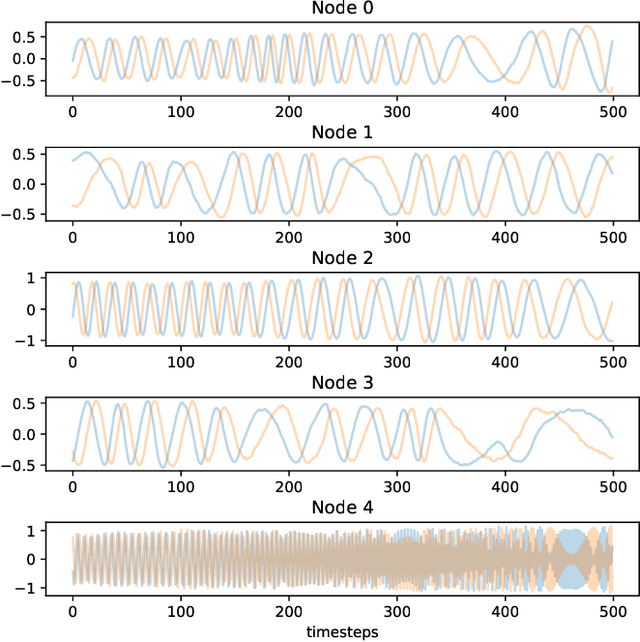
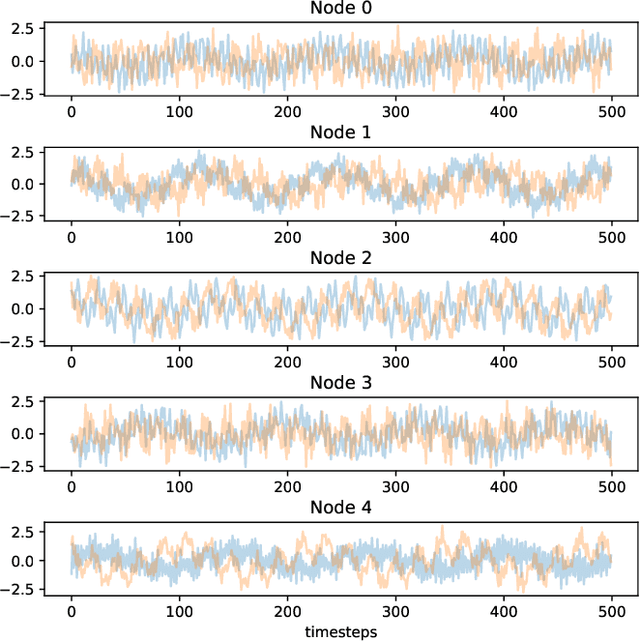
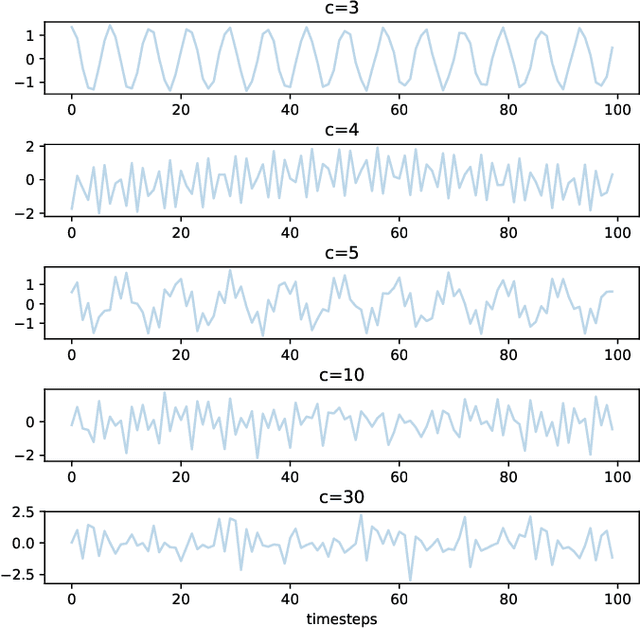
This paper proposes an autoregressive (AR) model for sequences of graphs, which generalises traditional AR models. A first novelty consists in formalising the AR model for a very general family of graphs, characterised by a variable topology, and attributes associated with nodes and edges. A graph neural network (GNN) is also proposed to learn the AR function associated with the graph-generating process (GGP), and subsequently predict the next graph in a sequence. The proposed method is compared with four baselines on synthetic GGPs, denoting a significantly better performance on all considered problems.