Hierarchical Representation Learning in Graph Neural Networks with Node Decimation Pooling
Paper and Code
Oct 24, 2019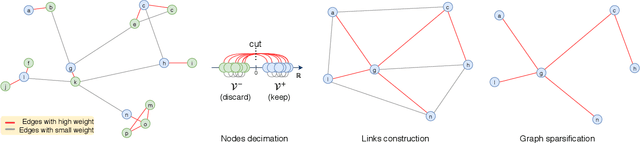
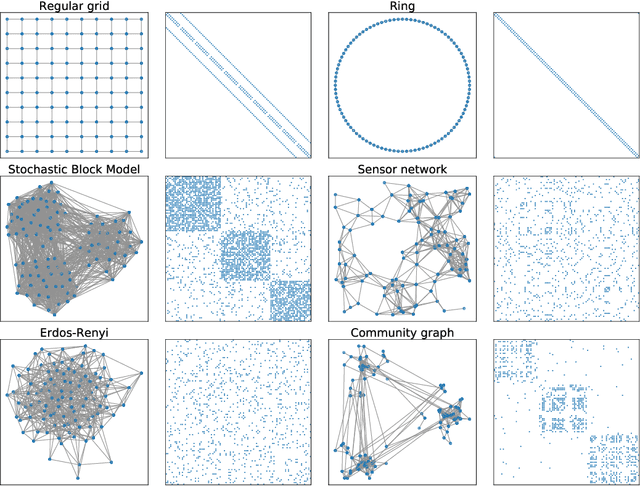
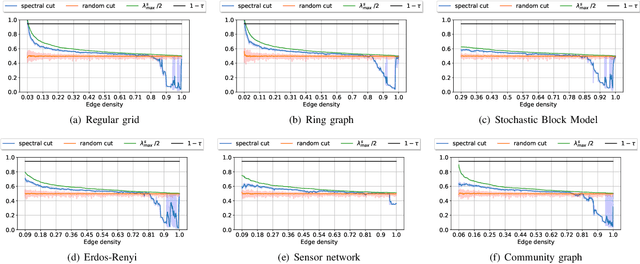
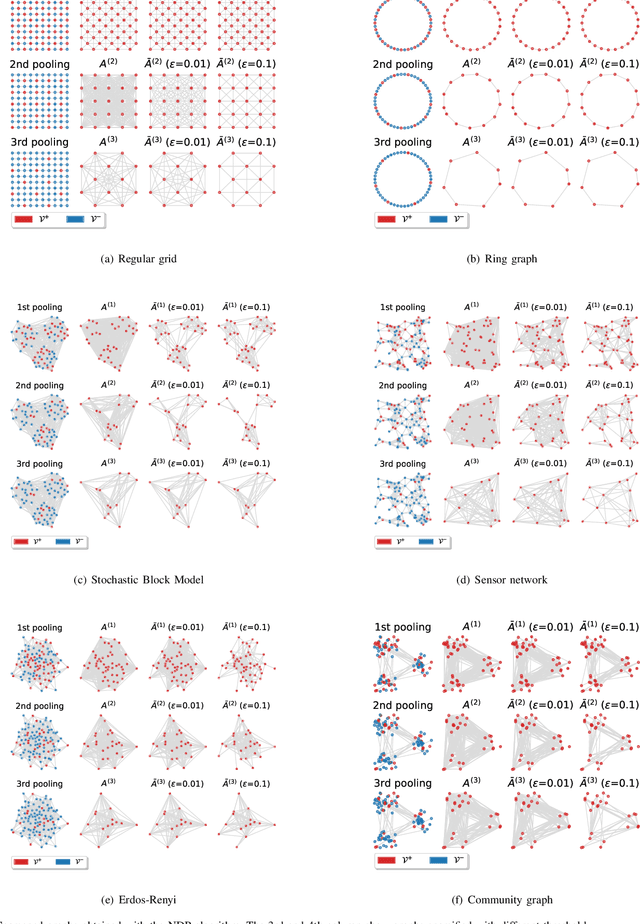
In graph neural networks (GNNs), pooling operators compute local summaries of input graphs to capture their global properties; in turn, they are fundamental operators for building deep GNNs that learn effective, hierarchical representations. In this work, we propose the Node Decimation Pooling (NDP), a pooling operator for GNNs that generates coarsened versions of a graph by leveraging on its topology only. During training, the GNN learns new representations for the vertices and fits them to a pyramid of coarsened graphs, which is computed in a pre-processing step. As theoretical contributions, we first demonstrate the equivalence between the MAXCUT partition and the node decimation procedure on which NDP is based. Then, we propose a procedure to sparsify the coarsened graphs for reducing the computational complexity in the GNN; we also demonstrate that it is possible to drop many edges without significantly altering the graph spectra of coarsened graphs. Experimental results show that NDP grants a significantly lower computational cost once compared to state-of-the-art graph pooling operators, while reaching, at the same time, competitive accuracy performance on a variety of graph classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge