Input representation in recurrent neural networks dynamics
Paper and Code
Mar 24, 2020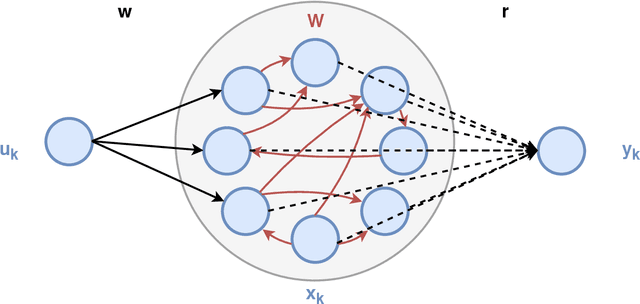
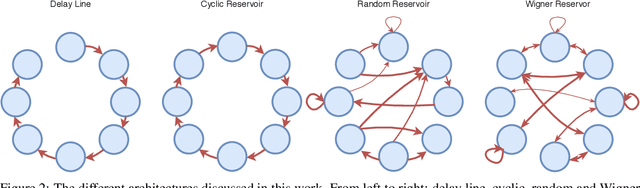
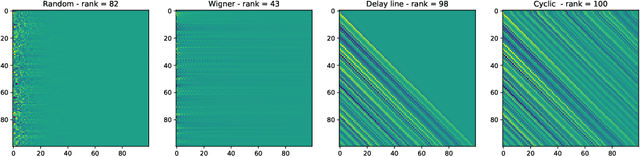
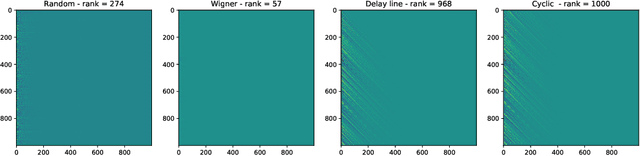
Reservoir computing is a popular approach to design recurrent neural networks, due to its training simplicity and its approximation performance. The recurrent part of these networks is not trained (e.g. via gradient descent), making them appealing for analytical studies, raising the interest of a vast community of researcher spanning from dynamical systems to neuroscience. It emerges that, even in the simple linear case, the working principle of these networks is not fully understood and the applied research is usually driven by heuristics. A novel analysis of the dynamics of such networks is proposed, which allows one to express the state evolution using the controllability matrix. Such a matrix encodes salient characteristics of the network dynamics: in particular, its rank can be used as an input-indepedent measure of the memory of the network. Using the proposed approach, it is possible to compare different architectures and explain why a cyclic topology achieves favourable results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge