Information Plane Analysis of Deep Neural Networks via Matrix-Based Renyi's Entropy and Tensor Kernels
Paper and Code
Sep 25, 2019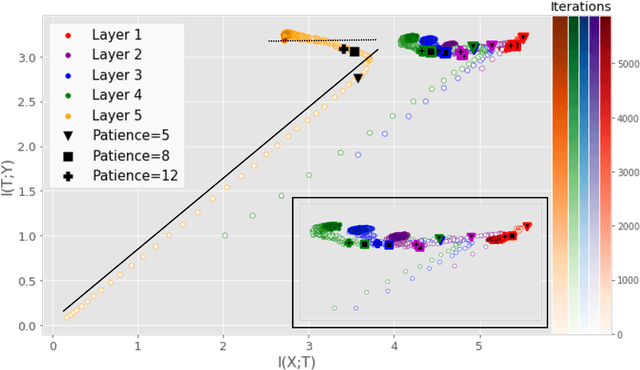
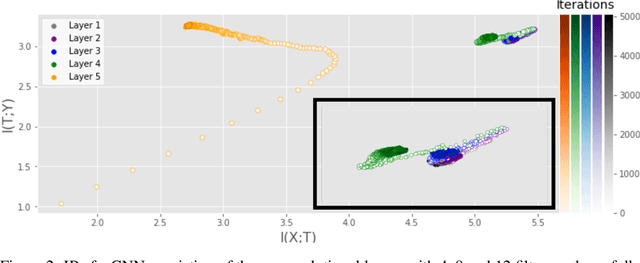
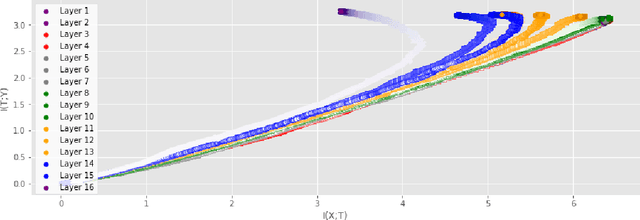
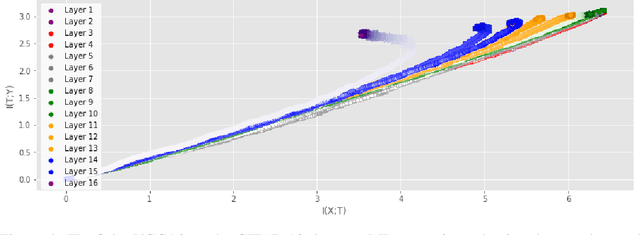
Analyzing deep neural networks (DNNs) via information plane (IP) theory has gained tremendous attention recently as a tool to gain insight into, among others, their generalization ability. However, it is by no means obvious how to estimate mutual information (MI) between each hidden layer and the input/desired output, to construct the IP. For instance, hidden layers with many neurons require MI estimators with robustness towards the high dimensionality associated with such layers. MI estimators should also be able to naturally handle convolutional layers, while at the same time being computationally tractable to scale to large networks. None of the existing IP methods to date have been able to study truly deep Convolutional Neural Networks (CNNs), such as the e.g.\ VGG-16. In this paper, we propose an IP analysis using the new matrix--based R\'enyi's entropy coupled with tensor kernels over convolutional layers, leveraging the power of kernel methods to represent properties of the probability distribution independently of the dimensionality of the data. The obtained results shed new light on the previous literature concerning small-scale DNNs, however using a completely new approach. Importantly, the new framework enables us to provide the first comprehensive IP analysis of contemporary large-scale DNNs and CNNs, investigating the different training phases and providing new insights into the training dynamics of large-scale neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge