Deep Transformed Gaussian Processes

Transformed Gaussian Processes (TGPs) are stochastic processes specified by transforming samples from the joint distribution from a prior process (typically a GP) using an invertible transformation; increasing the flexibility of the base process. Furthermore, they achieve competitive results compared with Deep Gaussian Processes (DGPs), which are another generalization constructed by a hierarchical concatenation of GPs. In this work, we propose a generalization of TGPs named Deep Transformed Gaussian Processes (DTGPs), which follows the trend of concatenating layers of stochastic processes. More precisely, we obtain a multi-layer model in which each layer is a TGP. This generalization implies an increment of flexibility with respect to both TGPs and DGPs. Exact inference in such a model is intractable. However, we show that one can use variational inference to approximate the required computations yielding a straightforward extension of the popular DSVI inference algorithm Salimbeni et al (2017). The experiments conducted evaluate the proposed novel DTGPs in multiple regression datasets, achieving good scalability and performance.

Towards Efficient Modeling and Inference in Multi-Dimensional Gaussian Process State-Space Models

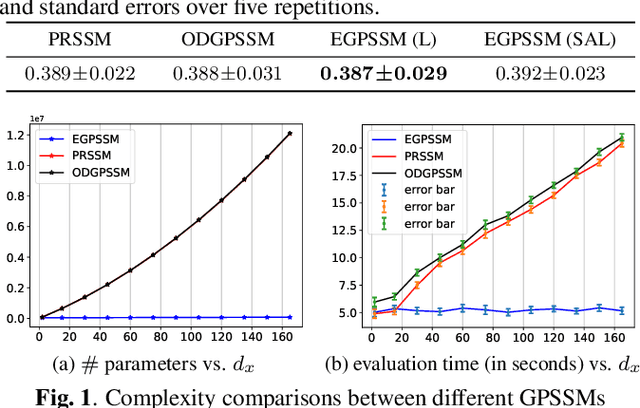
The Gaussian process state-space model (GPSSM) has attracted extensive attention for modeling complex nonlinear dynamical systems. However, the existing GPSSM employs separate Gaussian processes (GPs) for each latent state dimension, leading to escalating computational complexity and parameter proliferation, thus posing challenges for modeling dynamical systems with high-dimensional latent states. To surmount this obstacle, we propose to integrate the efficient transformed Gaussian process (ETGP) into the GPSSM, which involves pushing a shared GP through multiple normalizing flows to efficiently model the transition function in high-dimensional latent state space. Additionally, we develop a corresponding variational inference algorithm that surpasses existing methods in terms of parameter count and computational complexity. Experimental results on diverse synthetic and real-world datasets corroborate the efficiency of the proposed method, while also demonstrating its ability to achieve similar inference performance compared to existing methods. Code is available at \url{https://github.com/zhidilin/gpssmProj}.

Adaptive Temperature Scaling for Robust Calibration of Deep Neural Networks

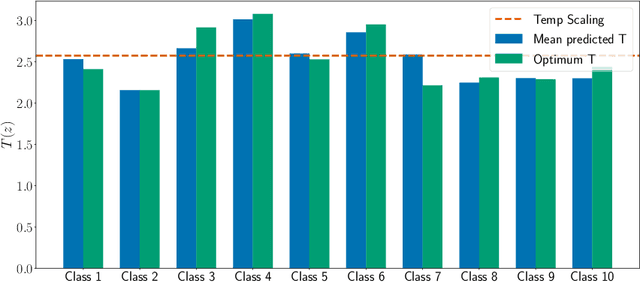
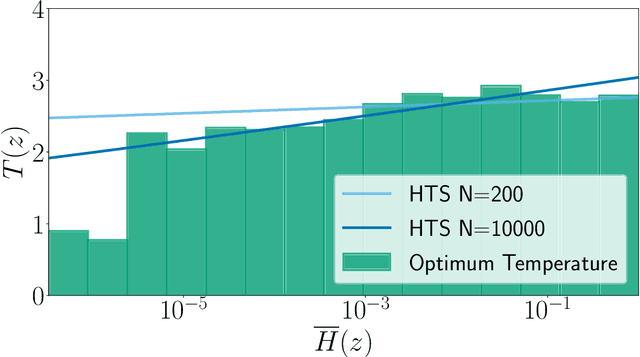
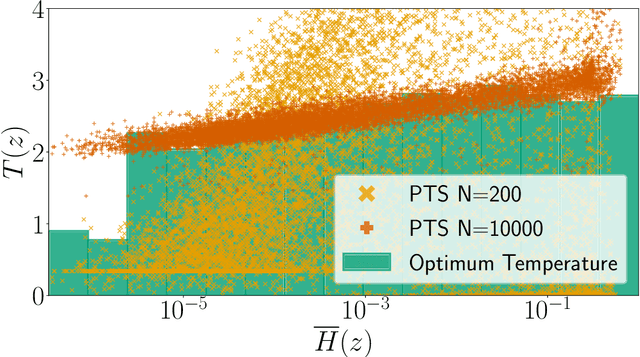
In this paper, we study the post-hoc calibration of modern neural networks, a problem that has drawn a lot of attention in recent years. Many calibration methods of varying complexity have been proposed for the task, but there is no consensus about how expressive these should be. We focus on the task of confidence scaling, specifically on post-hoc methods that generalize Temperature Scaling, we call these the Adaptive Temperature Scaling family. We analyse expressive functions that improve calibration and propose interpretable methods. We show that when there is plenty of data complex models like neural networks yield better performance, but are prone to fail when the amount of data is limited, a common situation in certain post-hoc calibration applications like medical diagnosis. We study the functions that expressive methods learn under ideal conditions and design simpler methods but with a strong inductive bias towards these well-performing functions. Concretely, we propose Entropy-based Temperature Scaling, a simple method that scales the confidence of a prediction according to its entropy. Results show that our method obtains state-of-the-art performance when compared to others and, unlike complex models, it is robust against data scarcity. Moreover, our proposed model enables a deeper interpretation of the calibration process.

Efficient Transformed Gaussian Processes for Non-Stationary Dependent Multi-class Classification

This work introduces the Efficient Transformed Gaussian Process (ETGP), a new way of creating C stochastic processes characterized by: 1) the C processes are non-stationary, 2) the C processes are dependent by construction without needing a mixing matrix, 3) training and making predictions is very efficient since the number of Gaussian Processes (GP) operations (e.g. inverting the inducing point's covariance matrix) do not depend on the number of processes. This makes the ETGP particularly suited for multi-class problems with a very large number of classes, which are the problems studied in this work. ETGPs exploit the recently proposed Transformed Gaussian Process (TGP), a stochastic process specified by transforming a Gaussian Process using an invertible transformation. However, unlike TGPs, ETGPs are constructed by transforming a single sample from a GP using C invertible transformations. We derive an efficient sparse variational inference algorithm for the proposed model and demonstrate its utility in 5 classification tasks which include low/medium/large datasets and a different number of classes, ranging from just a few to hundreds. Our results show that ETGPs, in general, outperform state-of-the-art methods for multi-class classification based on GPs, and have a lower computational cost (around one order of magnitude smaller).

Transforming Gaussian Processes With Normalizing Flows

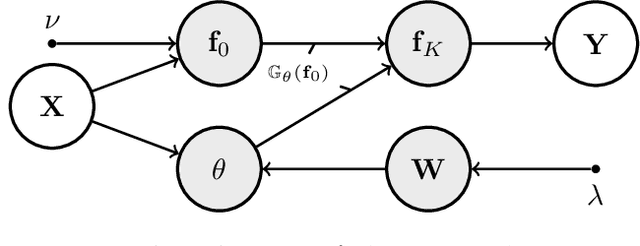
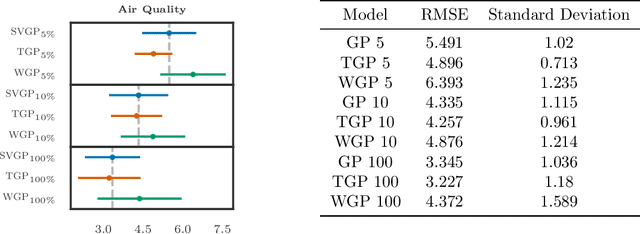
Gaussian Processes (GPs) can be used as flexible, non-parametric function priors. Inspired by the growing body of work on Normalizing Flows, we enlarge this class of priors through a parametric invertible transformation that can be made input-dependent. Doing so also allows us to encode interpretable prior knowledge (e.g., boundedness constraints). We derive a variational approximation to the resulting Bayesian inference problem, which is as fast as stochastic variational GP regression (Hensman et al., 2013; Dezfouli and Bonilla,2015). This makes the model a computationally efficient alternative to other hierarchical extensions of GP priors (Lazaro-Gredilla,2012; Damianou and Lawrence, 2013). The resulting algorithm's computational and inferential performance is excellent, and we demonstrate this on a range of data sets. For example, even with only 5 inducing points and an input-dependent flow, our method is consistently competitive with a standard sparse GP fitted using 100 inducing points.

Improving Calibration in Mixup-trained Deep Neural Networks through Confidence-Based Loss Functions

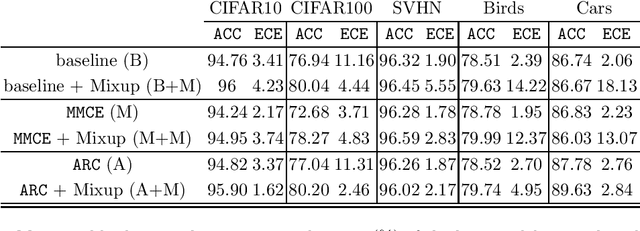
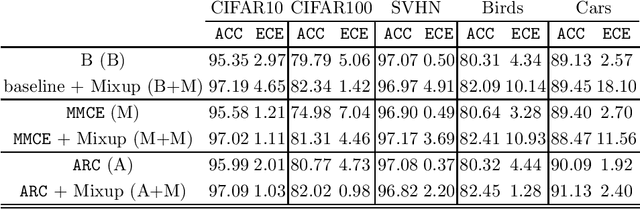
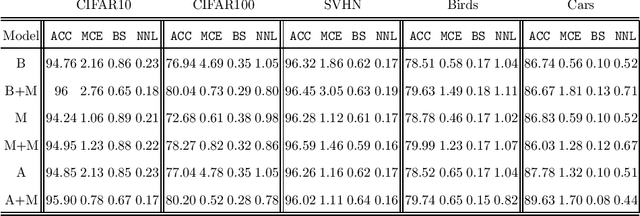
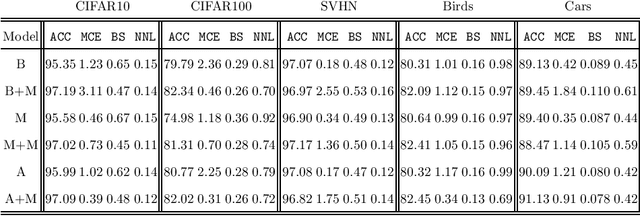
Deep Neural Networks (DNN) represent the state of the art in many tasks. However, due to their overparameterization, their generalization capabilities are in doubt and are still under study. Consequently, DNN can overfit and assign overconfident predictions, as they tend to learn highly oscillating decision thresholds. This has been shown to affect the calibration of the confidences assigned to unseen data. Data Augmentation (DA) strategies have been proposed to overcome some of these limitations. One of the most popular is Mixup, which has shown a great ability to improve the accuracy of these models. Recent work has provided evidence that Mixup also improves the uncertainty quantification and calibration of DNN. In this work, we argue and provide empirical evidence that, due to its fundamentals, Mixup does not necessarily improve calibration. Based on our observations we propose a new loss function that improves the calibration, and also sometimes the accuracy. Our loss is inspired by Bayes decision theory and introduces a new training framework for designing losses for probabilistic modelling. We provide state-of-the-art accuracy with consistent improvements in calibration performance.

Calibration of Deep Probabilistic Models with Decoupled Bayesian Neural Networks

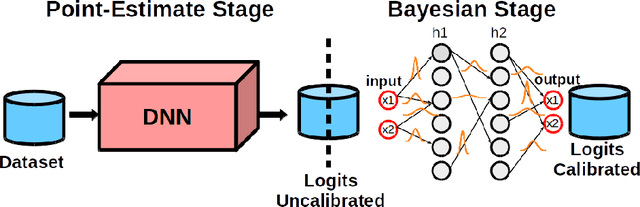
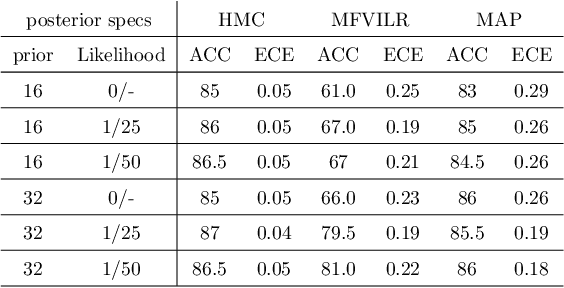
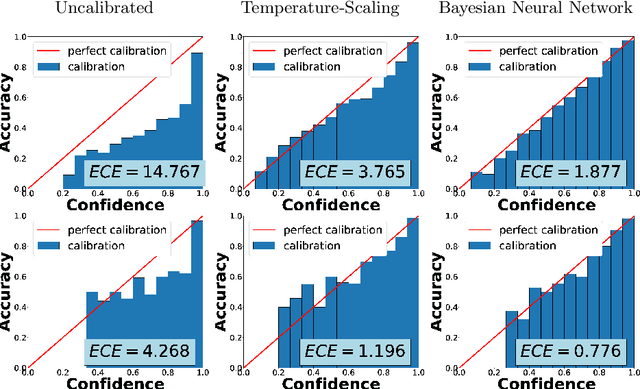
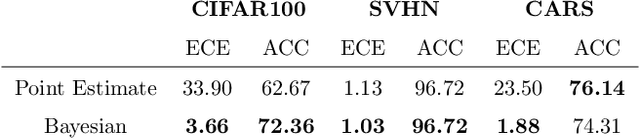
Deep Neural Networks (DNNs) have achieved state-of-the-art accuracy performance in many tasks. However, recent works have pointed out that the outputs provided by these models are not well-calibrated, seriously limiting their use in critical decision scenarios. In this work, we propose to use a decoupled Bayesian stage, implemented with a Bayesian Neural Network (BNN), to map the uncalibrated probabilities provided by a DNN to calibrated ones, consistently improving calibration. Our results evidence that incorporating uncertainty provides more reliable probabilistic models, a critical condition for achieving good calibration. We report a generous collection of experimental results using high-accuracy DNNs in standardized image classification benchmarks, showing the good performance, flexibility and robust behavior of our approach with respect to several state-of-the-art calibration methods. Code for reproducibility is provided.

Bayesian Strategies for Likelihood Ratio Computation in Forensic Voice Comparison with Automatic Systems

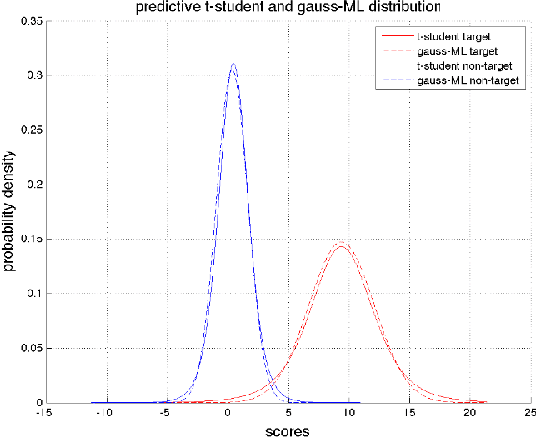
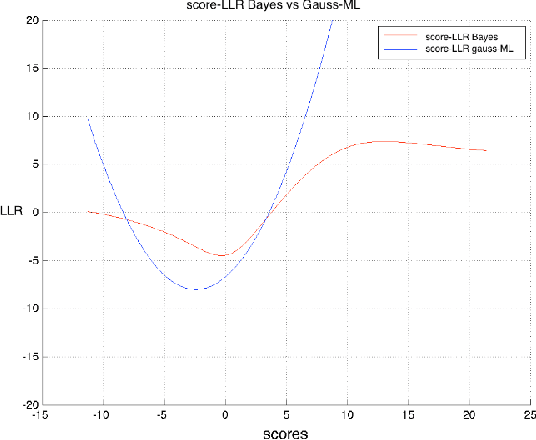
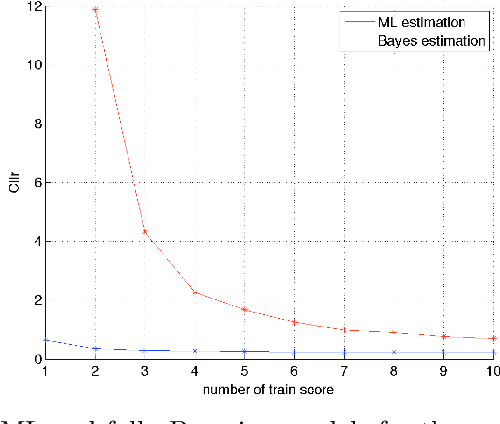
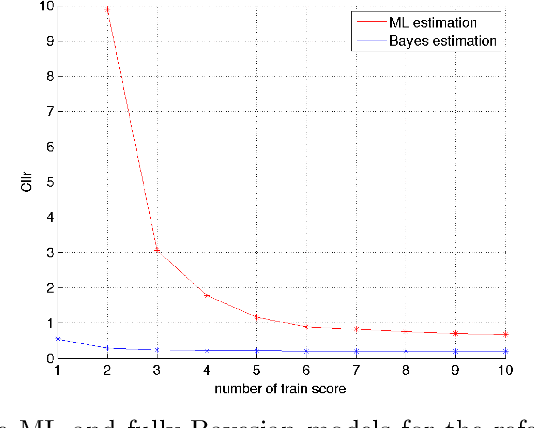
This paper explores several strategies for Forensic Voice Comparison (FVC), aimed at improving the performance of the LRs when using generative Gaussian score-to-LR models. First, different anchoring strategies are proposed, with the objective of adapting the LR computation process to the case at hand, always respecting the propositions defined for the particular case. Second, a fully-Bayesian Gaussian model is used to tackle the sparsity in the training scores that is often present when the proposed anchoring strategies are used. Experiments are performed using the 2014 i-Vector challenge set-up, which presents high variability in a telephone speech context. The results show that the proposed fully-Bayesian model clearly outperforms a more common Maximum-Likelihood approach, leading to high robustness when the scores to train the model become sparse.

Generative Models For Deep Learning with Very Scarce Data

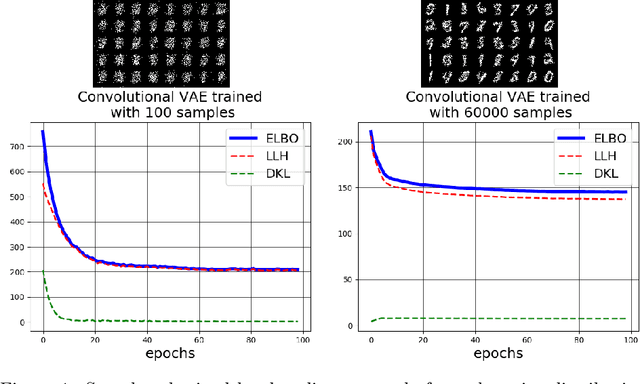
The goal of this paper is to deal with a data scarcity scenario where deep learning techniques use to fail. We compare the use of two well established techniques, Restricted Boltzmann Machines and Variational Auto-encoders, as generative models in order to increase the training set in a classification framework. Essentially, we rely on Markov Chain Monte Carlo (MCMC) algorithms for generating new samples. We show that generalization can be improved comparing this methodology to other state-of-the-art techniques, e.g. semi-supervised learning with ladder networks. Furthermore, we show that RBM is better than VAE generating new samples for training a classifier with good generalization capabilities.