Towards Efficient Modeling and Inference in Multi-Dimensional Gaussian Process State-Space Models
Paper and Code
Sep 03, 2023
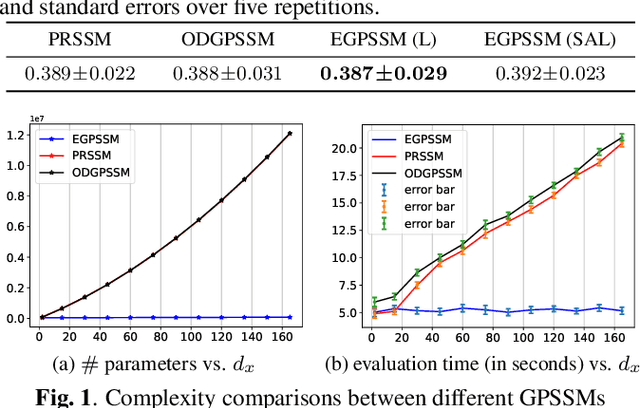

The Gaussian process state-space model (GPSSM) has attracted extensive attention for modeling complex nonlinear dynamical systems. However, the existing GPSSM employs separate Gaussian processes (GPs) for each latent state dimension, leading to escalating computational complexity and parameter proliferation, thus posing challenges for modeling dynamical systems with high-dimensional latent states. To surmount this obstacle, we propose to integrate the efficient transformed Gaussian process (ETGP) into the GPSSM, which involves pushing a shared GP through multiple normalizing flows to efficiently model the transition function in high-dimensional latent state space. Additionally, we develop a corresponding variational inference algorithm that surpasses existing methods in terms of parameter count and computational complexity. Experimental results on diverse synthetic and real-world datasets corroborate the efficiency of the proposed method, while also demonstrating its ability to achieve similar inference performance compared to existing methods. Code is available at \url{https://github.com/zhidilin/gpssmProj}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge