Deep Variational Implicit Processes
Paper and Code
Jun 14, 2022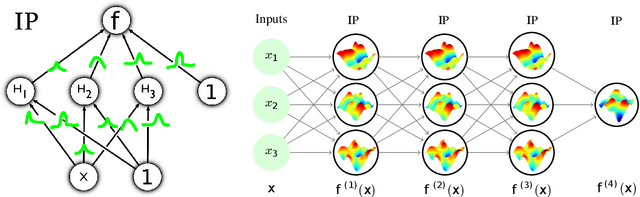
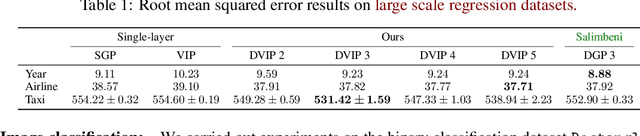
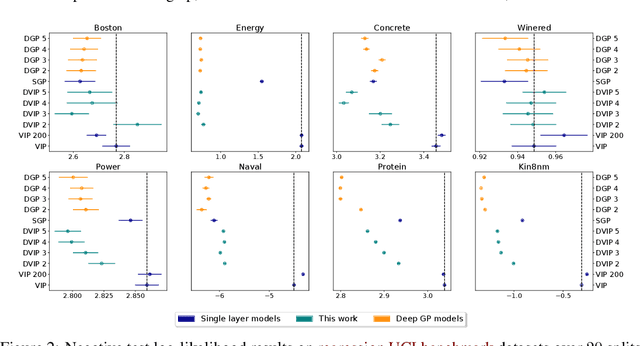

Implicit processes (IPs) are a generalization of Gaussian processes (GPs). IPs may lack a closed-form expression but are easy to sample from. Examples include, among others, Bayesian neural networks or neural samplers. IPs can be used as priors over functions, resulting in flexible models with well-calibrated prediction uncertainty estimates. Methods based on IPs usually carry out function-space approximate inference, which overcomes some of the difficulties of parameter-space approximate inference. Nevertheless, the approximations employed often limit the expressiveness of the final model, resulting, \emph{e.g.}, in a Gaussian predictive distribution, which can be restrictive. We propose here a multi-layer generalization of IPs called the Deep Variational Implicit process (DVIP). This generalization is similar to that of deep GPs over GPs, but it is more flexible due to the use of IPs as the prior distribution over the latent functions. We describe a scalable variational inference algorithm for training DVIP and show that it outperforms previous IP-based methods and also deep GPs. We support these claims via extensive regression and classification experiments. We also evaluate DVIP on large datasets with up to several million data instances to illustrate its good scalability and performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge