Speeding-up Evolutionary Algorithms to solve Black-Box Optimization Problems
Paper and Code
Sep 23, 2023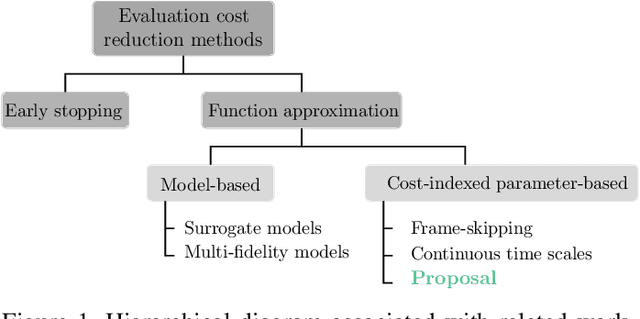
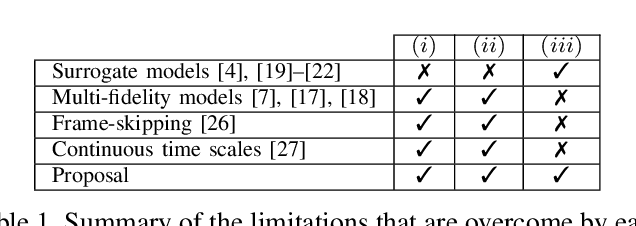
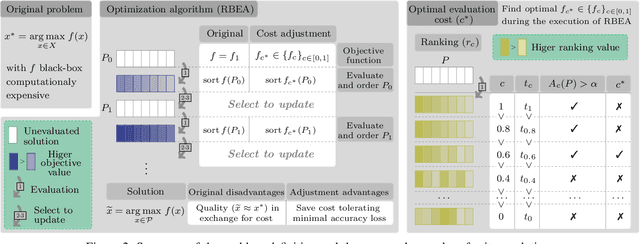
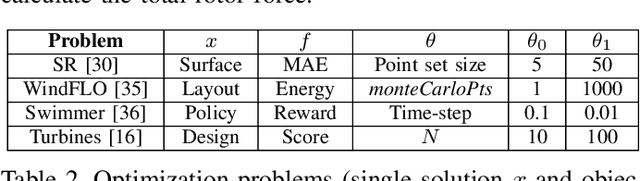
Population-based evolutionary algorithms are often considered when approaching computationally expensive black-box optimization problems. They employ a selection mechanism to choose the best solutions from a given population after comparing their objective values, which are then used to generate the next population. This iterative process explores the solution space efficiently, leading to improved solutions over time. However, these algorithms require a large number of evaluations to provide a quality solution, which might be computationally expensive when the evaluation cost is high. In some cases, it is possible to replace the original objective function with a less accurate approximation of lower cost. This introduces a trade-off between the evaluation cost and its accuracy. In this paper, we propose a technique capable of choosing an appropriate approximate function cost during the execution of the optimization algorithm. The proposal finds the minimum evaluation cost at which the solutions are still properly ranked, and consequently, more evaluations can be computed in the same amount of time with minimal accuracy loss. An experimental section on four very different problems reveals that the proposed approach can reach the same objective value in less than half of the time in certain cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge