Towards More Robust NLP System Evaluation: Handling Missing Scores in Benchmarks

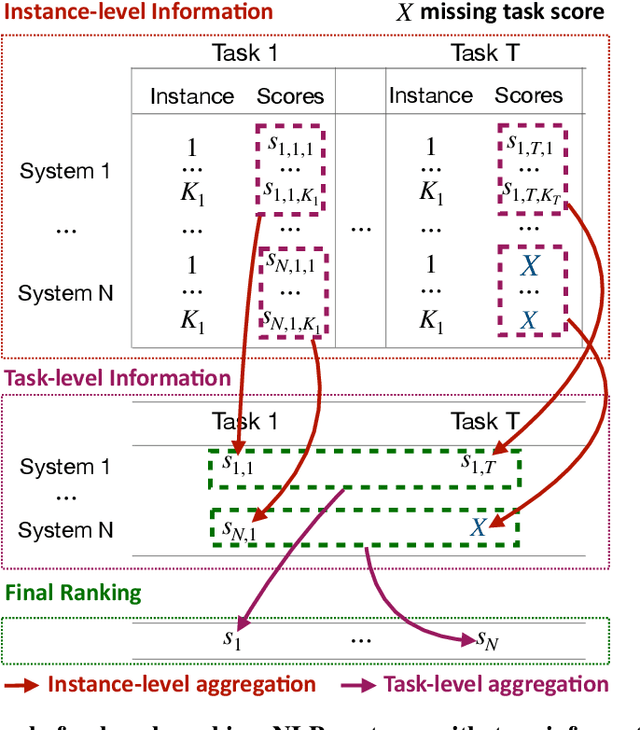
The evaluation of natural language processing (NLP) systems is crucial for advancing the field, but current benchmarking approaches often assume that all systems have scores available for all tasks, which is not always practical. In reality, several factors such as the cost of running baseline, private systems, computational limitations, or incomplete data may prevent some systems from being evaluated on entire tasks. This paper formalize an existing problem in NLP research: benchmarking when some systems scores are missing on the task, and proposes a novel approach to address it. Our method utilizes a compatible partial ranking approach to impute missing data, which is then aggregated using the Borda count method. It includes two refinements designed specifically for scenarios where either task-level or instance-level scores are available. We also introduce an extended benchmark, which contains over 131 million scores, an order of magnitude larger than existing benchmarks. We validate our methods and demonstrate their effectiveness in addressing the challenge of missing system evaluation on an entire task. This work highlights the need for more comprehensive benchmarking approaches that can handle real-world scenarios where not all systems are evaluated on the entire task.

Robust Consensus in Ranking Data Analysis: Definitions, Properties and Computational Issues

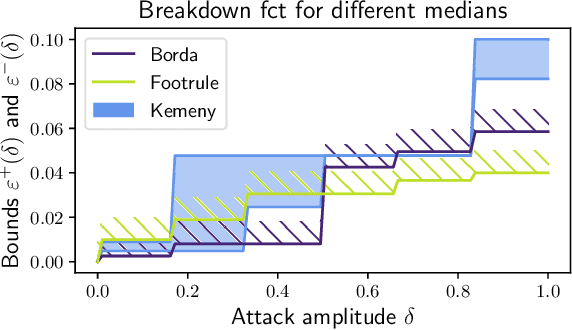
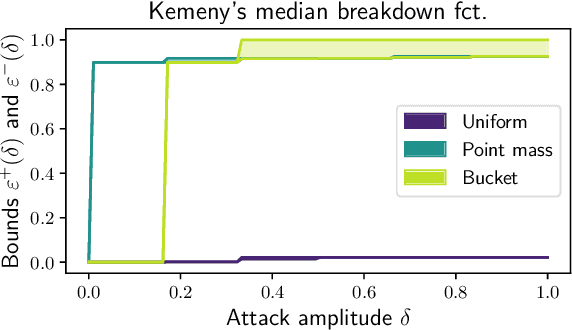
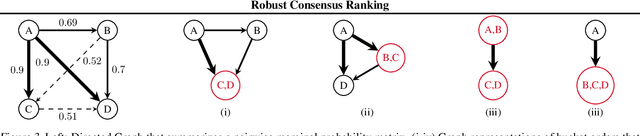
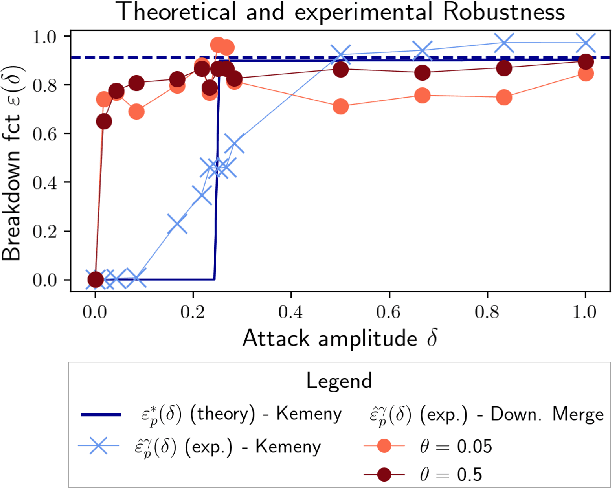
As the issue of robustness in AI systems becomes vital, statistical learning techniques that are reliable even in presence of partly contaminated data have to be developed. Preference data, in the form of (complete) rankings in the simplest situations, are no exception and the demand for appropriate concepts and tools is all the more pressing given that technologies fed by or producing this type of data (e.g. search engines, recommending systems) are now massively deployed. However, the lack of vector space structure for the set of rankings (i.e. the symmetric group $\mathfrak{S}_n$) and the complex nature of statistics considered in ranking data analysis make the formulation of robustness objectives in this domain challenging. In this paper, we introduce notions of robustness, together with dedicated statistical methods, for Consensus Ranking the flagship problem in ranking data analysis, aiming at summarizing a probability distribution on $\mathfrak{S}_n$ by a median ranking. Precisely, we propose specific extensions of the popular concept of breakdown point, tailored to consensus ranking, and address the related computational issues. Beyond the theoretical contributions, the relevance of the approach proposed is supported by an experimental study.

What are the best systems? New perspectives on NLP Benchmarking

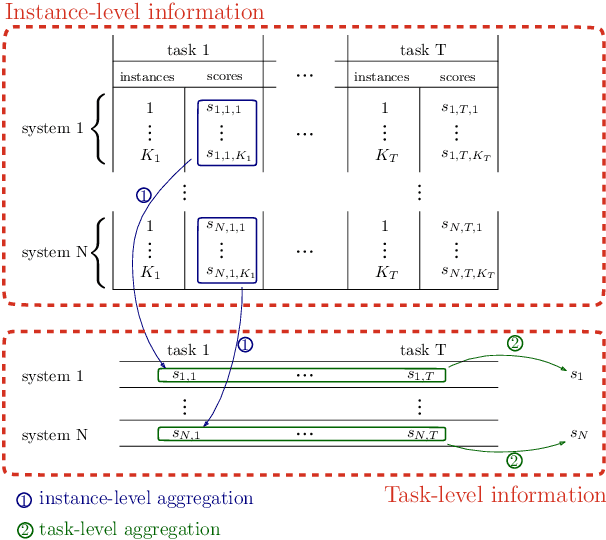
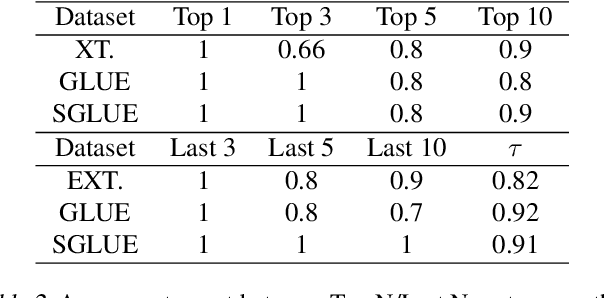
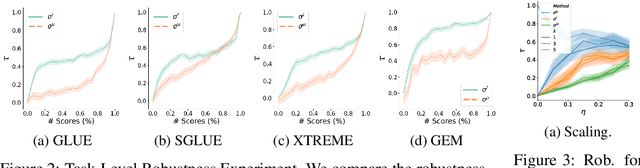
In Machine Learning, a benchmark refers to an ensemble of datasets associated with one or multiple metrics together with a way to aggregate different systems performances. They are instrumental in (i) assessing the progress of new methods along different axes and (ii) selecting the best systems for practical use. This is particularly the case for NLP with the development of large pre-trained models (e.g. GPT, BERT) that are expected to generalize well on a variety of tasks. While the community mainly focused on developing new datasets and metrics, there has been little interest in the aggregation procedure, which is often reduced to a simple average over various performance measures. However, this procedure can be problematic when the metrics are on a different scale, which may lead to spurious conclusions. This paper proposes a new procedure to rank systems based on their performance across different tasks. Motivated by the social choice theory, the final system ordering is obtained through aggregating the rankings induced by each task and is theoretically grounded. We conduct extensive numerical experiments (on over 270k scores) to assess the soundness of our approach both on synthetic and real scores (e.g. GLUE, EXTREM, SEVAL, TAC, FLICKR). In particular, we show that our method yields different conclusions on state-of-the-art systems than the mean-aggregation procedure while being both more reliable and robust.

The First AI4TSP Competition: Learning to Solve Stochastic Routing Problems

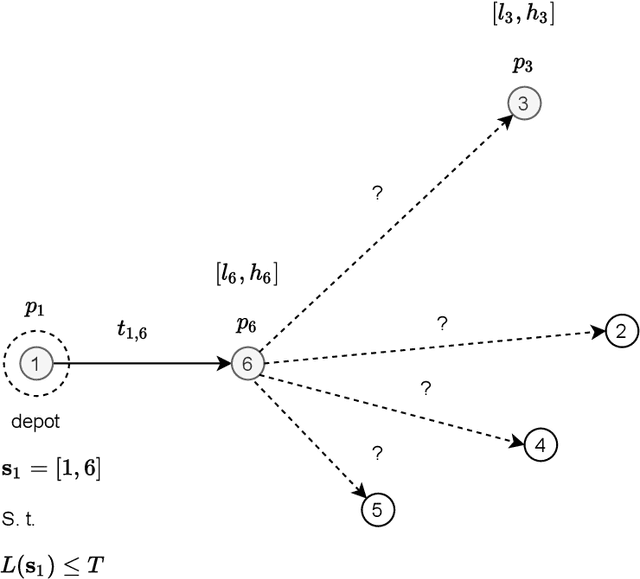
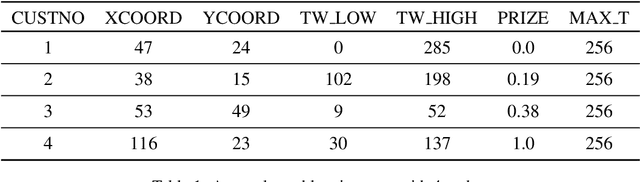
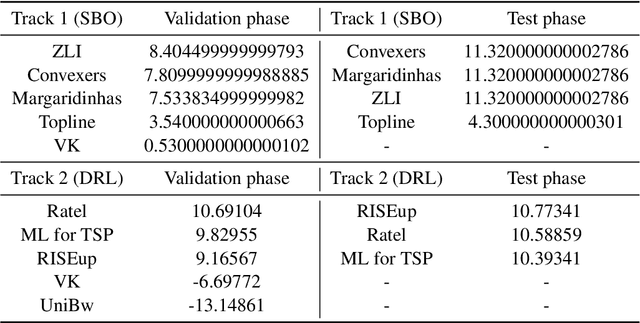
This paper reports on the first international competition on AI for the traveling salesman problem (TSP) at the International Joint Conference on Artificial Intelligence 2021 (IJCAI-21). The TSP is one of the classical combinatorial optimization problems, with many variants inspired by real-world applications. This first competition asked the participants to develop algorithms to solve a time-dependent orienteering problem with stochastic weights and time windows (TD-OPSWTW). It focused on two types of learning approaches: surrogate-based optimization and deep reinforcement learning. In this paper, we describe the problem, the setup of the competition, the winning methods, and give an overview of the results. The winning methods described in this work have advanced the state-of-the-art in using AI for stochastic routing problems. Overall, by organizing this competition we have introduced routing problems as an interesting problem setting for AI researchers. The simulator of the problem has been made open-source and can be used by other researchers as a benchmark for new AI methods.

Statistical Depth Functions for Ranking Distributions: Definitions, Statistical Learning and Applications

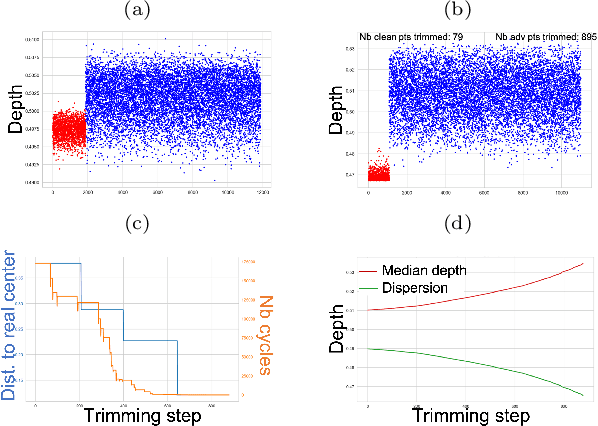
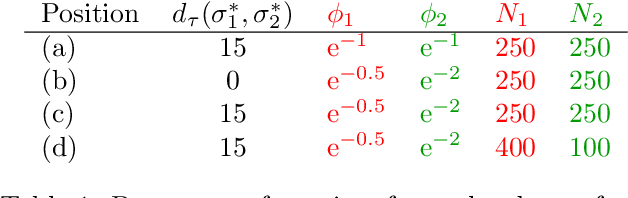
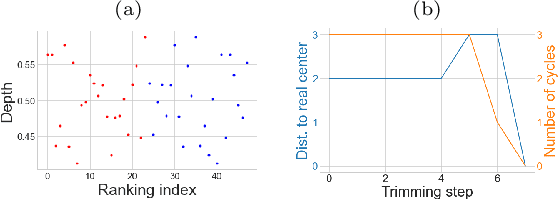
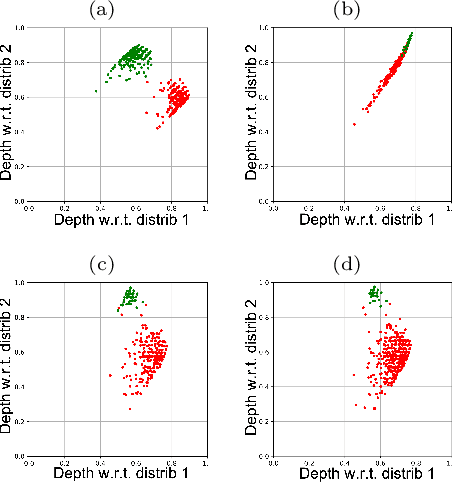
The concept of median/consensus has been widely investigated in order to provide a statistical summary of ranking data, i.e. realizations of a random permutation $\Sigma$ of a finite set, $\{1,\; \ldots,\; n\}$ with $n\geq 1$ say. As it sheds light onto only one aspect of $\Sigma$'s distribution $P$, it may neglect other informative features. It is the purpose of this paper to define analogs of quantiles, ranks and statistical procedures based on such quantities for the analysis of ranking data by means of a metric-based notion of depth function on the symmetric group. Overcoming the absence of vector space structure on $\mathfrak{S}_n$, the latter defines a center-outward ordering of the permutations in the support of $P$ and extends the classic metric-based formulation of consensus ranking (medians corresponding then to the deepest permutations). The axiomatic properties that ranking depths should ideally possess are listed, while computational and generalization issues are studied at length. Beyond the theoretical analysis carried out, the relevance of the novel concepts and methods introduced for a wide variety of statistical tasks are also supported by numerous numerical experiments.

Kernels of Mallows Models under the Hamming Distance for solving the Quadratic Assignment Problem

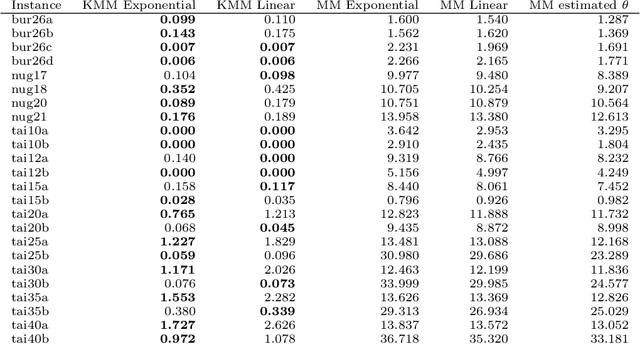
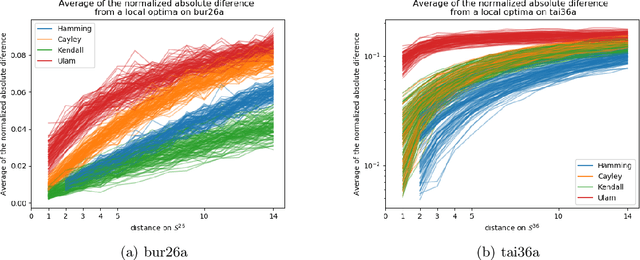
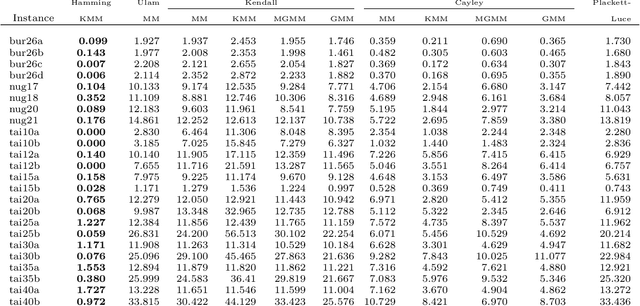
The Quadratic Assignment Problem (QAP) is a well-known permutation-based combinatorial optimization problem with real applications in industrial and logistics environments. Motivated by the challenge that this NP-hard problem represents, it has captured the attention of the evolutionary computation community for decades. As a result, a large number of algorithms have been proposed to optimize this algorithm. Among these, exact methods are only able to solve instances of size $n<40$, and thus, many heuristic and metaheuristic methods have been applied to the QAP. In this work, we follow this direction by approaching the QAP through Estimation of Distribution Algorithms (EDAs). Particularly, a non-parametric distance-based exponential probabilistic model is used. Based on the analysis of the characteristics of the QAP, and previous work in the area, we introduce Kernels of Mallows Model under the Hamming distance to the context of EDAs. Conducted experiments point out that the performance of the proposed algorithm in the QAP is superior to (i) the classical EDAs adapted to deal with the QAP, and also (ii) to the specific EDAs proposed in the literature to deal with permutation problems.

Online Ranking with Concept Drifts in Streaming Data

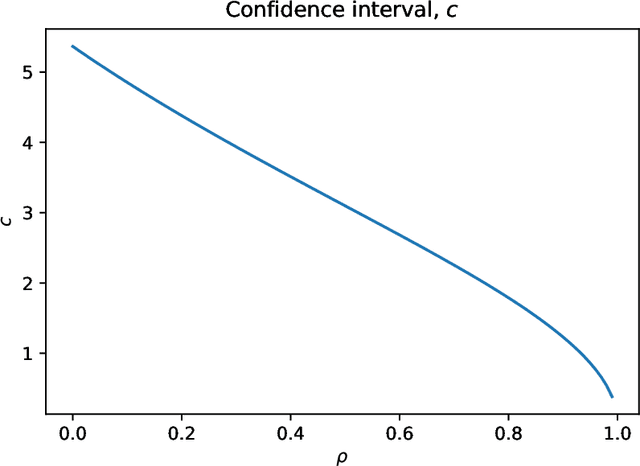
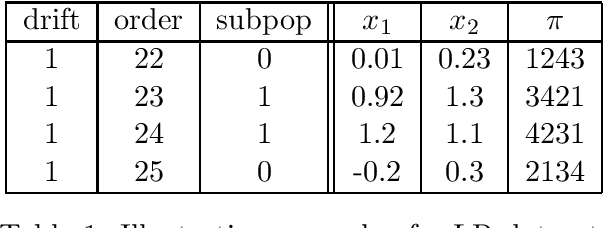
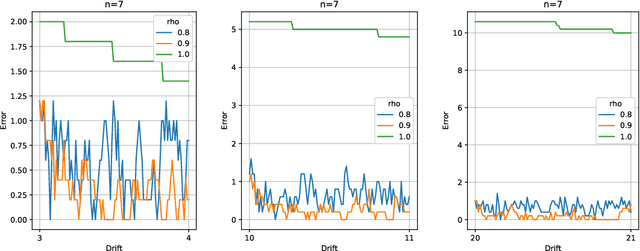
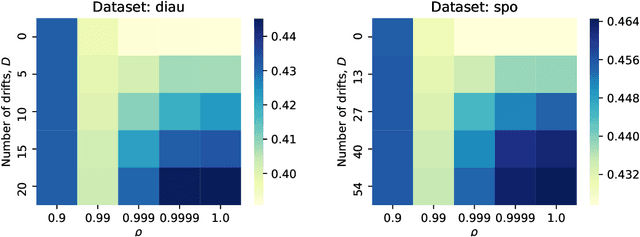
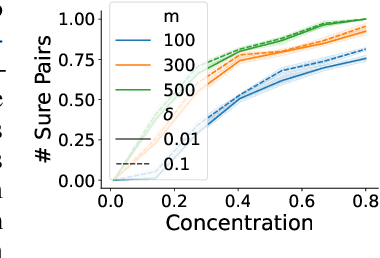
Two important problems in preference elicitation are rank aggregation and label ranking. Rank aggregation consists of finding a ranking that best summarizes a collection of preferences of some agents. The latter, label ranking, aims at learning a mapping between data instances and rankings defined over a finite set of categories or labels. This problem can effectively model many real application scenarios such as recommender systems. However, even when the preferences of populations usually change over time, related literature has so far addressed both problems over non-evolving preferences. This work deals with the problems of rank aggregation and label ranking over non-stationary data streams. In this context, there is a set of $n$ items and $m$ agents which provide their votes by casting a ranking of the $n$ items. The rankings are noisy realizations of an unknown probability distribution that changes over time. Our goal is to learn, in an online manner, the current ground truth distribution of rankings. We begin by proposing an aggregation function called Forgetful Borda (FBorda) that, using a forgetting mechanism, gives more importance to recently observed preferences. We prove that FBorda is a consistent estimator of the Kemeny ranking and lower bound the number of samples needed to learn the distribution while guaranteeing a certain level of confidence. Then, we develop a $k$-nearest neighbor classifier based on the proposed FBorda aggregation algorithm for the label ranking problem and demonstrate its accuracy in several scenarios of label ranking problem over evolving preferences.