Towards More Robust NLP System Evaluation: Handling Missing Scores in Benchmarks

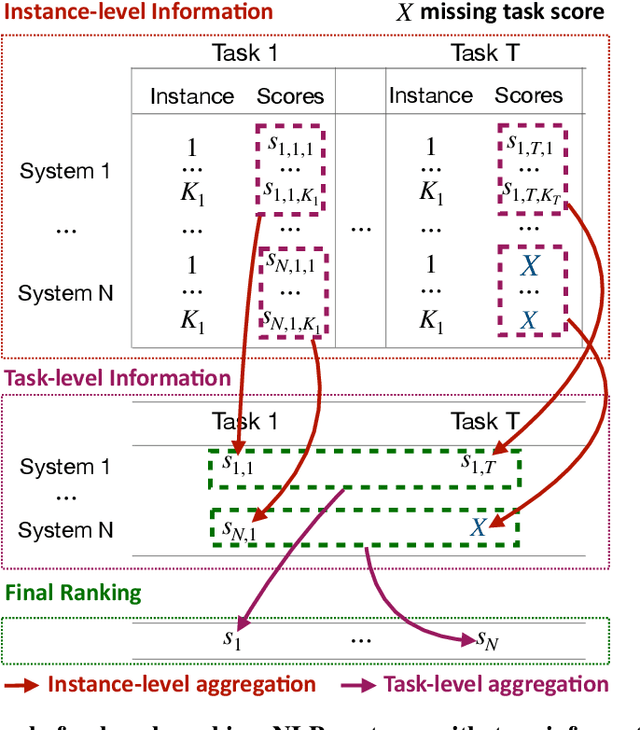
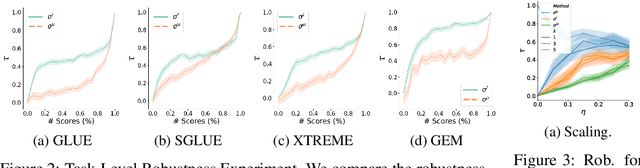
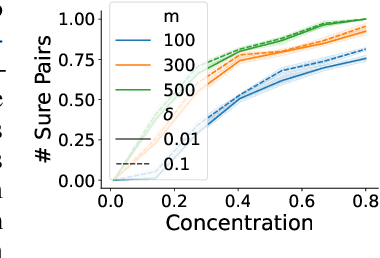
The evaluation of natural language processing (NLP) systems is crucial for advancing the field, but current benchmarking approaches often assume that all systems have scores available for all tasks, which is not always practical. In reality, several factors such as the cost of running baseline, private systems, computational limitations, or incomplete data may prevent some systems from being evaluated on entire tasks. This paper formalize an existing problem in NLP research: benchmarking when some systems scores are missing on the task, and proposes a novel approach to address it. Our method utilizes a compatible partial ranking approach to impute missing data, which is then aggregated using the Borda count method. It includes two refinements designed specifically for scenarios where either task-level or instance-level scores are available. We also introduce an extended benchmark, which contains over 131 million scores, an order of magnitude larger than existing benchmarks. We validate our methods and demonstrate their effectiveness in addressing the challenge of missing system evaluation on an entire task. This work highlights the need for more comprehensive benchmarking approaches that can handle real-world scenarios where not all systems are evaluated on the entire task.

What are the best systems? New perspectives on NLP Benchmarking

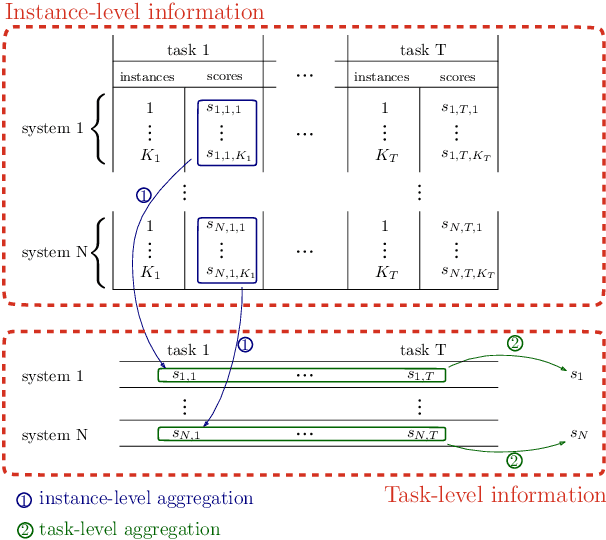
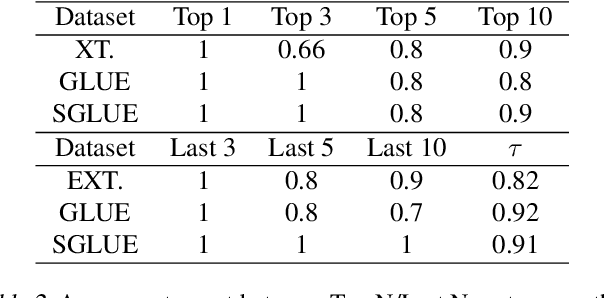
In Machine Learning, a benchmark refers to an ensemble of datasets associated with one or multiple metrics together with a way to aggregate different systems performances. They are instrumental in (i) assessing the progress of new methods along different axes and (ii) selecting the best systems for practical use. This is particularly the case for NLP with the development of large pre-trained models (e.g. GPT, BERT) that are expected to generalize well on a variety of tasks. While the community mainly focused on developing new datasets and metrics, there has been little interest in the aggregation procedure, which is often reduced to a simple average over various performance measures. However, this procedure can be problematic when the metrics are on a different scale, which may lead to spurious conclusions. This paper proposes a new procedure to rank systems based on their performance across different tasks. Motivated by the social choice theory, the final system ordering is obtained through aggregating the rankings induced by each task and is theoretically grounded. We conduct extensive numerical experiments (on over 270k scores) to assess the soundness of our approach both on synthetic and real scores (e.g. GLUE, EXTREM, SEVAL, TAC, FLICKR). In particular, we show that our method yields different conclusions on state-of-the-art systems than the mean-aggregation procedure while being both more reliable and robust.

AUC Optimisation and Collaborative Filtering

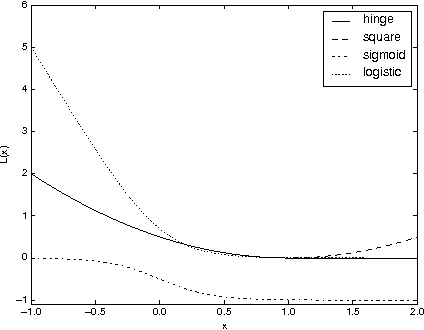
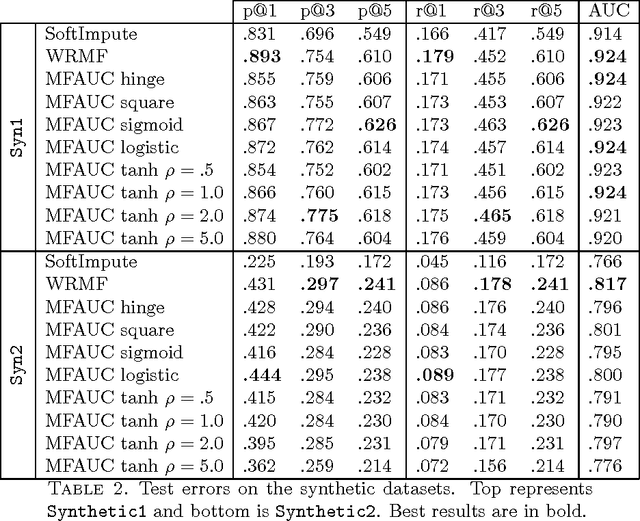
In recommendation systems, one is interested in the ranking of the predicted items as opposed to other losses such as the mean squared error. Although a variety of ways to evaluate rankings exist in the literature, here we focus on the Area Under the ROC Curve (AUC) as it widely used and has a strong theoretical underpinning. In practical recommendation, only items at the top of the ranked list are presented to the users. With this in mind, we propose a class of objective functions over matrix factorisations which primarily represent a smooth surrogate for the real AUC, and in a special case we show how to prioritise the top of the list. The objectives are differentiable and optimised through a carefully designed stochastic gradient-descent-based algorithm which scales linearly with the size of the data. In the special case of square loss we show how to improve computational complexity by leveraging previously computed measures. To understand theoretically the underlying matrix factorisation approaches we study both the consistency of the loss functions with respect to AUC, and generalisation using Rademacher theory. The resulting generalisation analysis gives strong motivation for the optimisation under study. Finally, we provide computation results as to the efficacy of the proposed method using synthetic and real data.