Metrics and methods for a systematic comparison of fairness-aware machine learning algorithms

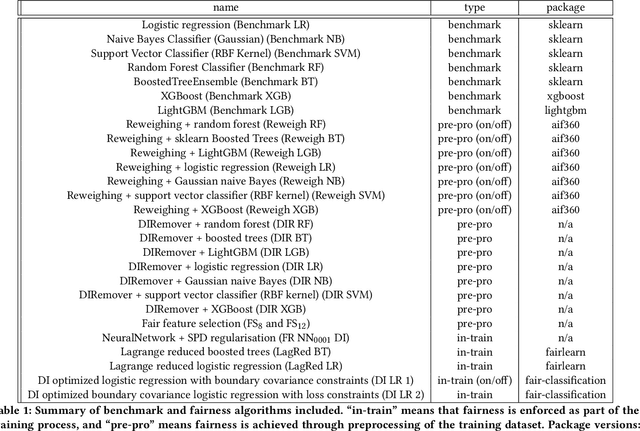
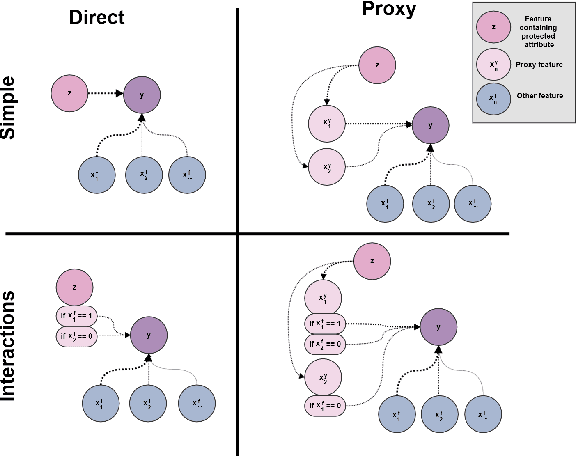
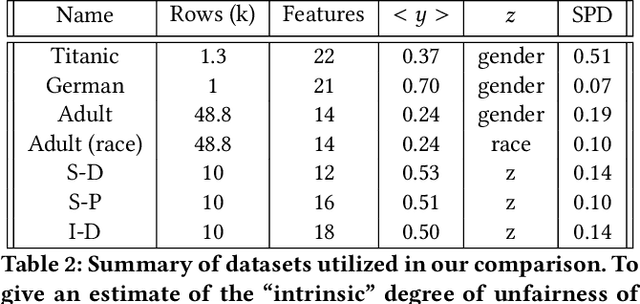
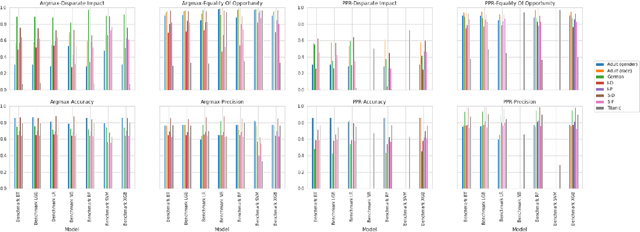
Understanding and removing bias from the decisions made by machine learning models is essential to avoid discrimination against unprivileged groups. Despite recent progress in algorithmic fairness, there is still no clear answer as to which bias-mitigation approaches are most effective. Evaluation strategies are typically use-case specific, rely on data with unclear bias, and employ a fixed policy to convert model outputs to decision outcomes. To address these problems, we performed a systematic comparison of a number of popular fairness algorithms applicable to supervised classification. Our study is the most comprehensive of its kind. It utilizes three real and four synthetic datasets, and two different ways of converting model outputs to decisions. It considers fairness, predictive-performance, calibration quality, and speed of 28 different modelling pipelines, corresponding to both fairness-unaware and fairness-aware algorithms. We found that fairness-unaware algorithms typically fail to produce adequately fair models and that the simplest algorithms are not necessarily the fairest ones. We also found that fairness-aware algorithms can induce fairness without material drops in predictive power. Finally, we found that dataset idiosyncracies (e.g., degree of intrinsic unfairness, nature of correlations) do affect the performance of fairness-aware approaches. Our results allow the practitioner to narrow down the approach(es) they would like to adopt without having to know in advance their fairness requirements.

AUC Optimisation and Collaborative Filtering

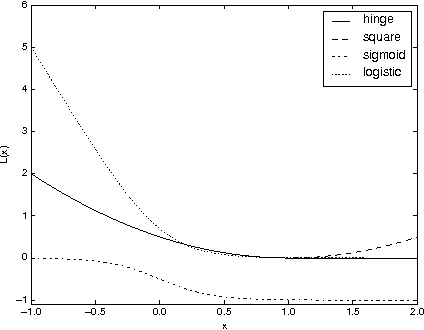
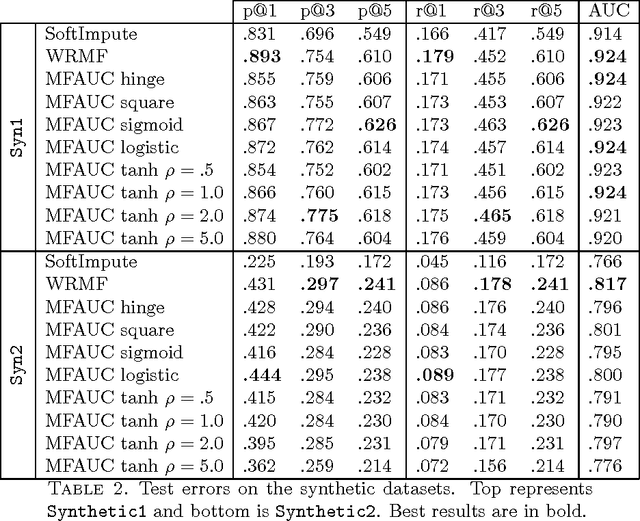
In recommendation systems, one is interested in the ranking of the predicted items as opposed to other losses such as the mean squared error. Although a variety of ways to evaluate rankings exist in the literature, here we focus on the Area Under the ROC Curve (AUC) as it widely used and has a strong theoretical underpinning. In practical recommendation, only items at the top of the ranked list are presented to the users. With this in mind, we propose a class of objective functions over matrix factorisations which primarily represent a smooth surrogate for the real AUC, and in a special case we show how to prioritise the top of the list. The objectives are differentiable and optimised through a carefully designed stochastic gradient-descent-based algorithm which scales linearly with the size of the data. In the special case of square loss we show how to improve computational complexity by leveraging previously computed measures. To understand theoretically the underlying matrix factorisation approaches we study both the consistency of the loss functions with respect to AUC, and generalisation using Rademacher theory. The resulting generalisation analysis gives strong motivation for the optimisation under study. Finally, we provide computation results as to the efficacy of the proposed method using synthetic and real data.

An SIR Graph Growth Model for the Epidemics of Communicable Diseases

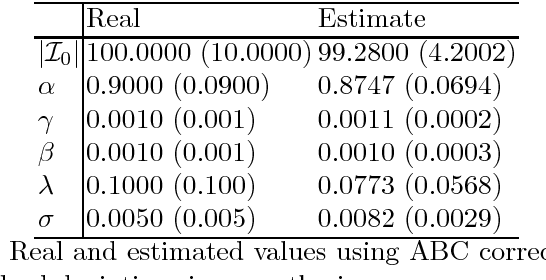
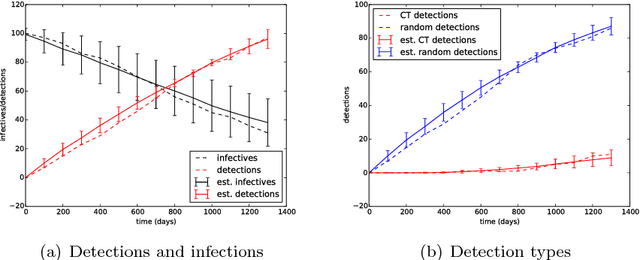
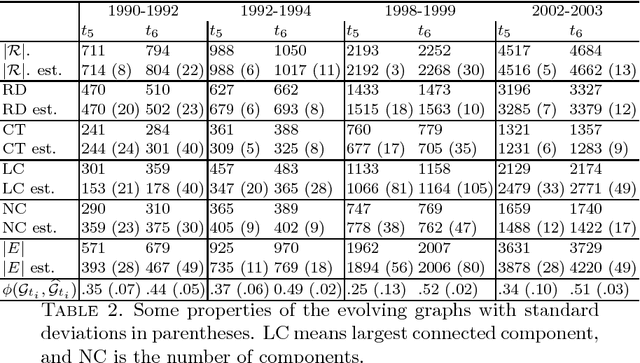
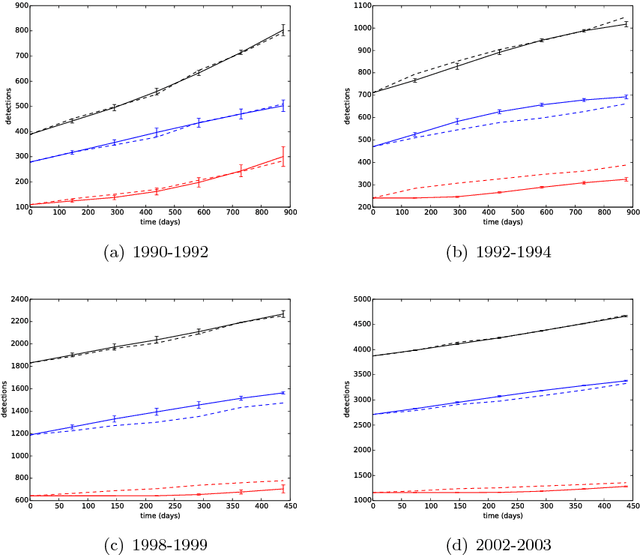
It is the main purpose of this paper to introduce a graph-valued stochastic process in order to model the spread of a communicable infectious disease. The major novelty of the SIR model we promote lies in the fact that the social network on which the epidemics is taking place is not specified in advance but evolves through time, accounting for the temporal evolution of the interactions involving infective individuals. Without assuming the existence of a fixed underlying network model, the stochastic process introduced describes, in a flexible and realistic manner, epidemic spread in non-uniformly mixing and possibly heterogeneous populations. It is shown how to fit such a (parametrised) model by means of Approximate Bayesian Computation methods based on graph-valued statistics. The concepts and statistical methods described in this paper are finally applied to a real epidemic dataset, related to the spread of HIV in Cuba in presence of a contact tracing system, which permits one to reconstruct partly the evolution of the graph of sexual partners diagnosed HIV positive between 1986 and 2006.

Efficient Eigen-updating for Spectral Graph Clustering

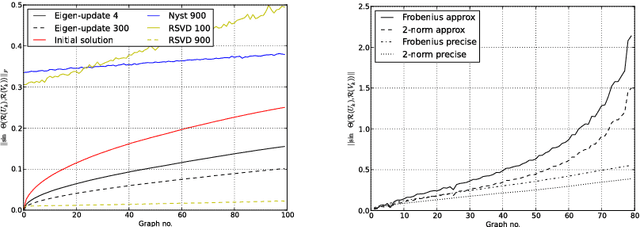
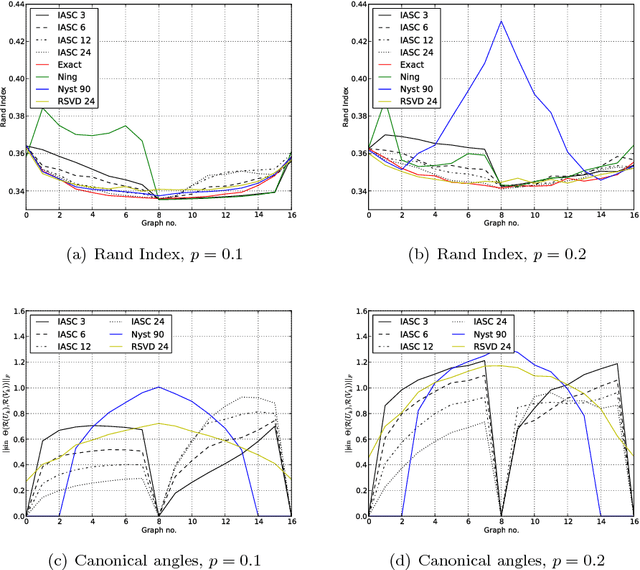
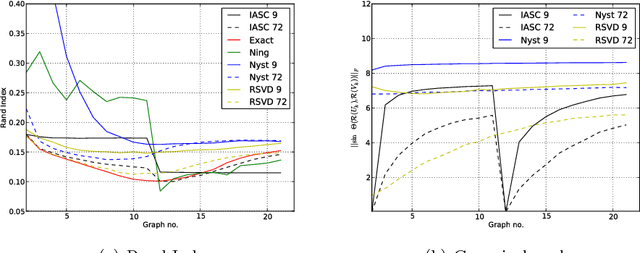
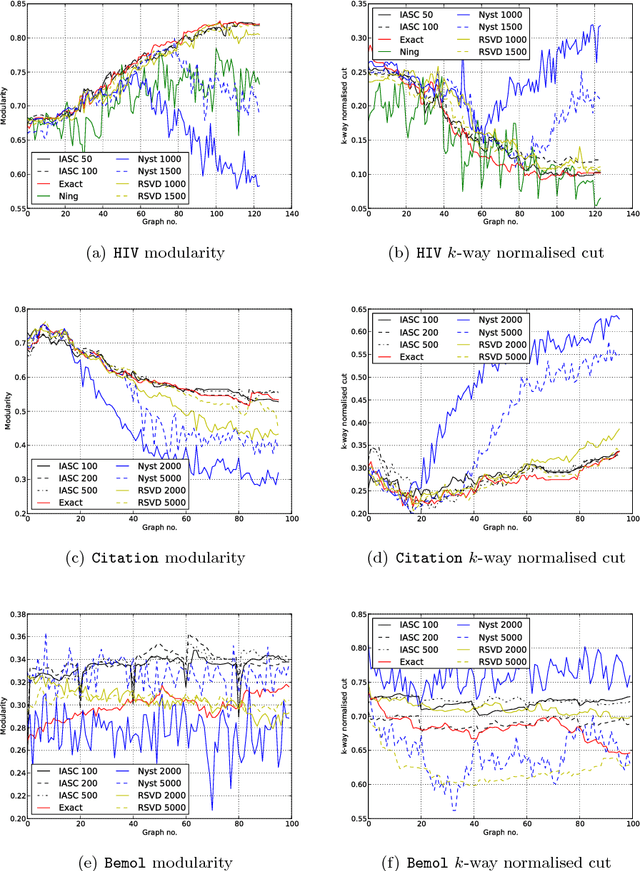
Partitioning a graph into groups of vertices such that those within each group are more densely connected than vertices assigned to different groups, known as graph clustering, is often used to gain insight into the organisation of large scale networks and for visualisation purposes. Whereas a large number of dedicated techniques have been recently proposed for static graphs, the design of on-line graph clustering methods tailored for evolving networks is a challenging problem, and much less documented in the literature. Motivated by the broad variety of applications concerned, ranging from the study of biological networks to the analysis of networks of scientific references through the exploration of communications networks such as the World Wide Web, it is the main purpose of this paper to introduce a novel, computationally efficient, approach to graph clustering in the evolutionary context. Namely, the method promoted in this article can be viewed as an incremental eigenvalue solution for the spectral clustering method described by Ng. et al. (2001). The incremental eigenvalue solution is a general technique for finding the approximate eigenvectors of a symmetric matrix given a change. As well as outlining the approach in detail, we present a theoretical bound on the quality of the approximate eigenvectors using perturbation theory. We then derive a novel spectral clustering algorithm called Incremental Approximate Spectral Clustering (IASC). The IASC algorithm is simple to implement and its efficacy is demonstrated on both synthetic and real datasets modelling the evolution of a HIV epidemic, a citation network and the purchase history graph of an e-commerce website.

Online Matrix Completion Through Nuclear Norm Regularisation

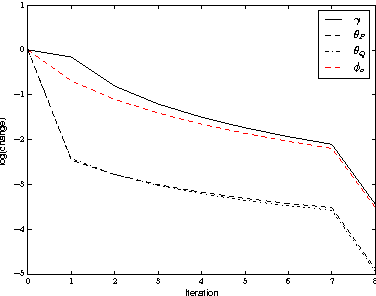
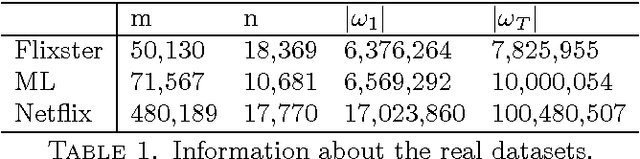
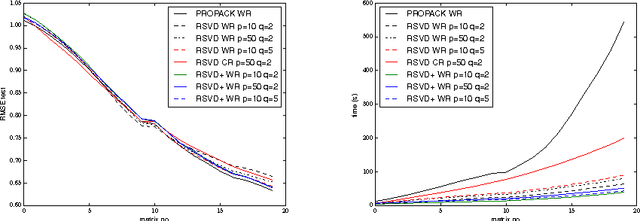
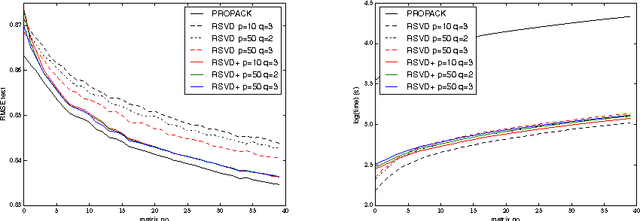
It is the main goal of this paper to propose a novel method to perform matrix completion on-line. Motivated by a wide variety of applications, ranging from the design of recommender systems to sensor network localization through seismic data reconstruction, we consider the matrix completion problem when entries of the matrix of interest are observed gradually. Precisely, we place ourselves in the situation where the predictive rule should be refined incrementally, rather than recomputed from scratch each time the sample of observed entries increases. The extension of existing matrix completion methods to the sequential prediction context is indeed a major issue in the Big Data era, and yet little addressed in the literature. The algorithm promoted in this article builds upon the Soft Impute approach introduced in Mazumder et al. (2010). The major novelty essentially arises from the use of a randomised technique for both computing and updating the Singular Value Decomposition (SVD) involved in the algorithm. Though of disarming simplicity, the method proposed turns out to be very efficient, while requiring reduced computations. Several numerical experiments based on real datasets illustrating its performance are displayed, together with preliminary results giving it a theoretical basis.

Learning Reputation in an Authorship Network

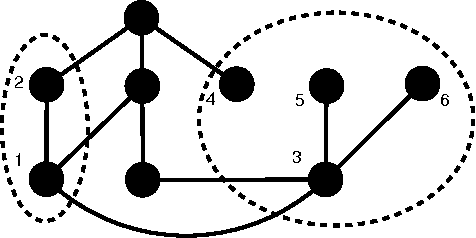
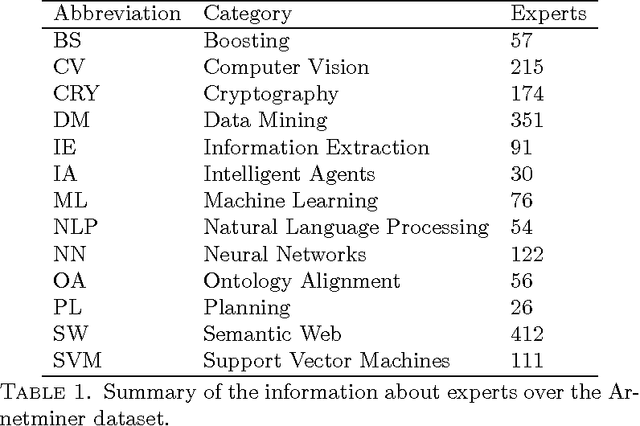
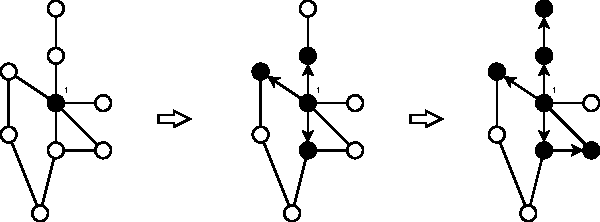
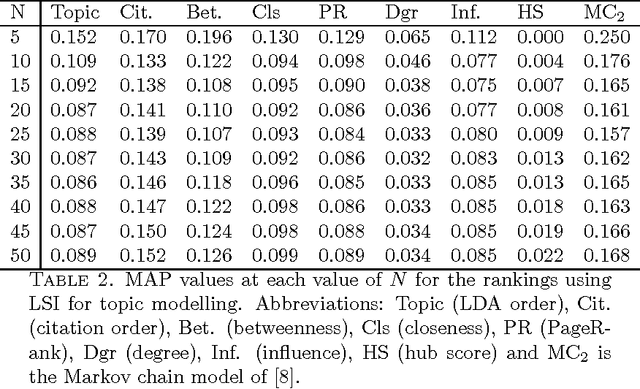
The problem of searching for experts in a given academic field is hugely important in both industry and academia. We study exactly this issue with respect to a database of authors and their publications. The idea is to use Latent Semantic Indexing (LSI) and Latent Dirichlet Allocation (LDA) to perform topic modelling in order to find authors who have worked in a query field. We then construct a coauthorship graph and motivate the use of influence maximisation and a variety of graph centrality measures to obtain a ranked list of experts. The ranked lists are further improved using a Markov Chain-based rank aggregation approach. The complete method is readily scalable to large datasets. To demonstrate the efficacy of the approach we report on an extensive set of computational simulations using the Arnetminer dataset. An improvement in mean average precision is demonstrated over the baseline case of simply using the order of authors found by the topic models.

An Empirical Comparison of V-fold Penalisation and Cross Validation for Model Selection in Distribution-Free Regression

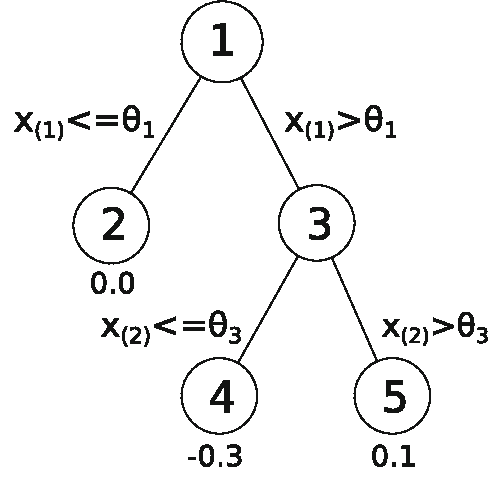
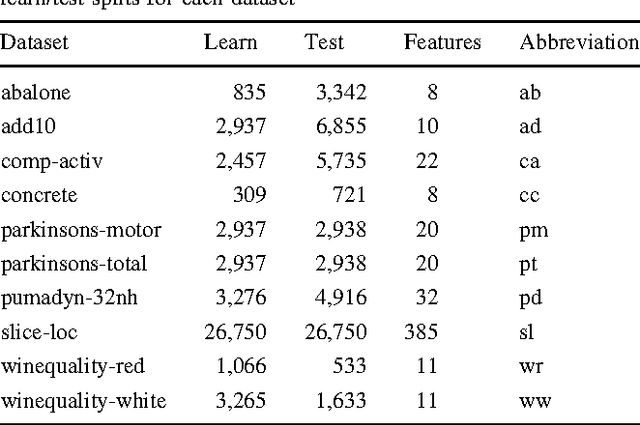
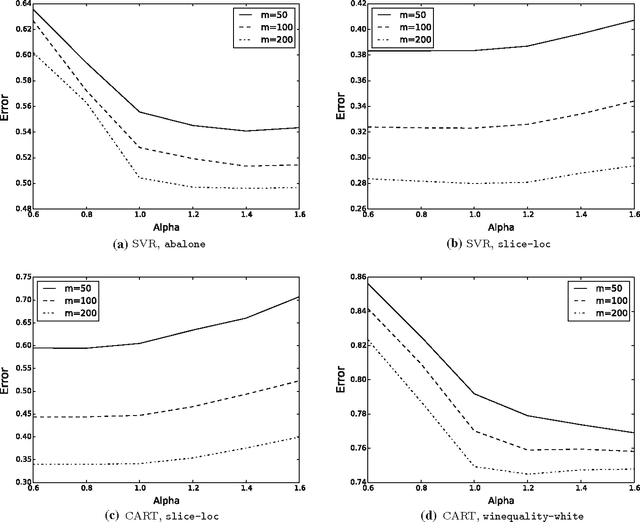
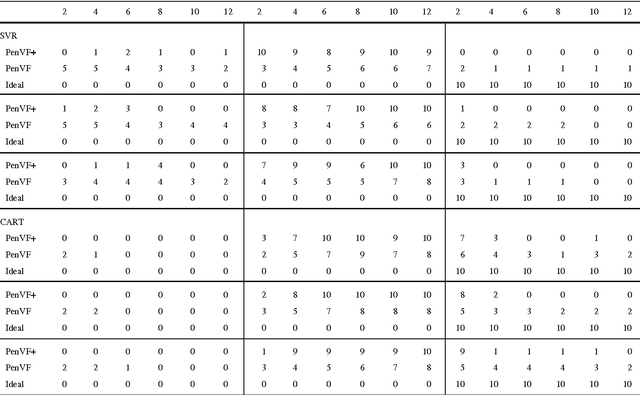
Model selection is a crucial issue in machine-learning and a wide variety of penalisation methods (with possibly data dependent complexity penalties) have recently been introduced for this purpose. However their empirical performance is generally not well documented in the literature. It is the goal of this paper to investigate to which extent such recent techniques can be successfully used for the tuning of both the regularisation and kernel parameters in support vector regression (SVR) and the complexity measure in regression trees (CART). This task is traditionally solved via V-fold cross-validation (VFCV), which gives efficient results for a reasonable computational cost. A disadvantage however of VFCV is that the procedure is known to provide an asymptotically suboptimal risk estimate as the number of examples tends to infinity. Recently, a penalisation procedure called V-fold penalisation has been proposed to improve on VFCV, supported by theoretical arguments. Here we report on an extensive set of experiments comparing V-fold penalisation and VFCV for SVR/CART calibration on several benchmark datasets. We highlight cases in which VFCV and V-fold penalisation provide poor estimates of the risk respectively and introduce a modified penalisation technique to reduce the estimation error.