Interpretable time series neural representation for classification purposes

Deep learning has made significant advances in creating efficient representations of time series data by automatically identifying complex patterns. However, these approaches lack interpretability, as the time series is transformed into a latent vector that is not easily interpretable. On the other hand, Symbolic Aggregate approximation (SAX) methods allow the creation of symbolic representations that can be interpreted but do not capture complex patterns effectively. In this work, we propose a set of requirements for a neural representation of univariate time series to be interpretable. We propose a new unsupervised neural architecture that meets these requirements. The proposed model produces consistent, discrete, interpretable, and visualizable representations. The model is learned independently of any downstream tasks in an unsupervised setting to ensure robustness. As a demonstration of the effectiveness of the proposed model, we propose experiments on classification tasks using UCR archive datasets. The obtained results are extensively compared to other interpretable models and state-of-the-art neural representation learning models. The experiments show that the proposed model yields, on average better results than other interpretable approaches on multiple datasets. We also present qualitative experiments to asses the interpretability of the approach.

Time Series Continuous Modeling for Imputation and Forecasting with Implicit Neural Representations

Although widely explored, time series modeling continues to encounter significant challenges when confronted with real-world data. We propose a novel modeling approach leveraging Implicit Neural Representations (INR). This approach enables us to effectively capture the continuous aspect of time series and provides a natural solution to recurring modeling issues such as handling missing data, dealing with irregular sampling, or unaligned observations from multiple sensors. By introducing conditional modulation of INR parameters and leveraging meta-learning techniques, we address the issue of generalization to both unseen samples and time window shifts. Through extensive experimentation, our model demonstrates state-of-the-art performance in forecasting and imputation tasks, while exhibiting flexibility in handling a wide range of challenging scenarios that competing models cannot.

Generalizing to New Physical Systems via Context-Informed Dynamics Model

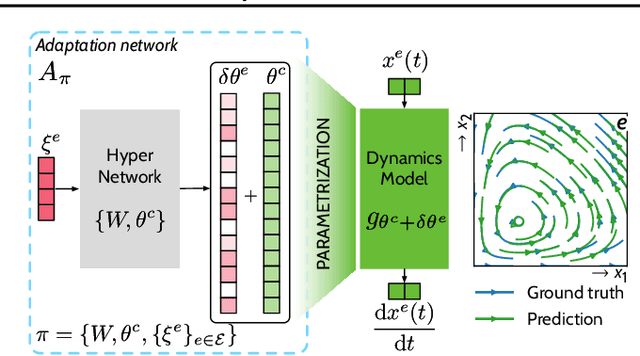
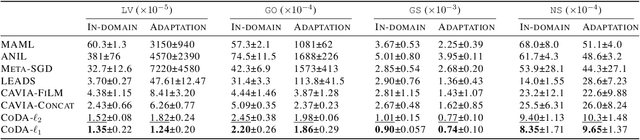
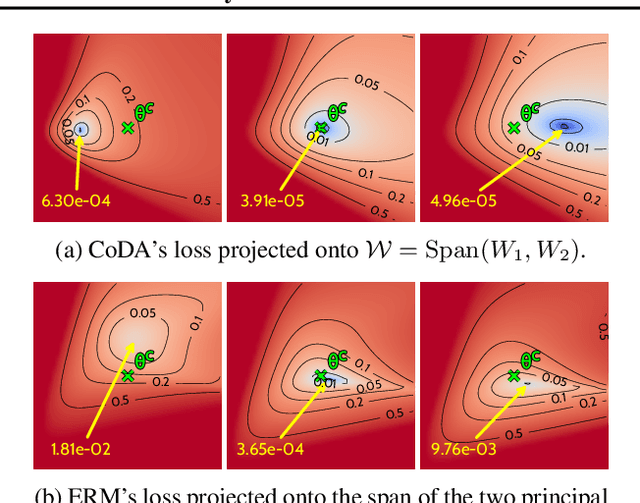
Data-driven approaches to modeling physical systems fail to generalize to unseen systems that share the same general dynamics with the learning domain, but correspond to different physical contexts. We propose a new framework for this key problem, context-informed dynamics adaptation (CoDA), which takes into account the distributional shift across systems for fast and efficient adaptation to new dynamics. CoDA leverages multiple environments, each associated to a different dynamic, and learns to condition the dynamics model on contextual parameters, specific to each environment. The conditioning is performed via a hypernetwork, learned jointly with a context vector from observed data. The proposed formulation constrains the search hypothesis space to foster fast adaptation and better generalization across environments. It extends the expressivity of existing methods. We theoretically motivate our approach and show state-ofthe-art generalization results on a set of nonlinear dynamics, representative of a variety of application domains. We also show, on these systems, that new system parameters can be inferred from context vectors with minimal supervision.

LEADS: Learning Dynamical Systems that Generalize Across Environments

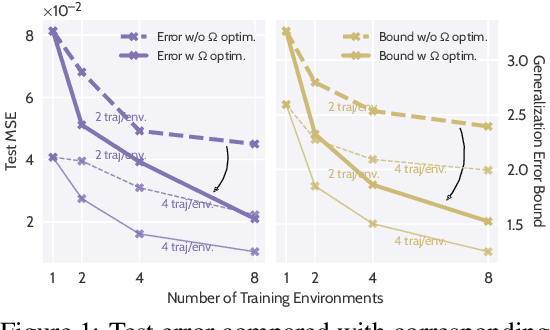
When modeling dynamical systems from real-world data samples, the distribution of data often changes according to the environment in which they are captured, and the dynamics of the system itself vary from one environment to another. Generalizing across environments thus challenges the conventional frameworks. The classical settings suggest either considering data as i.i.d. and learning a single model to cover all situations or learning environment-specific models. Both are sub-optimal: the former disregards the discrepancies between environments leading to biased solutions, while the latter does not exploit their potential commonalities and is prone to scarcity problems. We propose LEADS, a novel framework that leverages the commonalities and discrepancies among known environments to improve model generalization. This is achieved with a tailored training formulation aiming at capturing common dynamics within a shared model while additional terms capture environment-specific dynamics. We ground our approach in theory, exhibiting a decrease in sample complexity with our approach and corroborate these results empirically, instantiating it for linear dynamics. Moreover, we concretize this framework for neural networks and evaluate it experimentally on representative families of nonlinear dynamics. We show that this new setting can exploit knowledge extracted from environment-dependent data and improves generalization for both known and novel environments.

Binary Stochastic Representations for Large Multi-class Classification

Classification with a large number of classes is a key problem in machine learning and corresponds to many real-world applications like tagging of images or textual documents in social networks. If one-vs-all methods usually reach top performance in this context, these approaches suffer from a high inference complexity, linear w.r.t the number of categories. Different models based on the notion of binary codes have been proposed to overcome this limitation, achieving in a sublinear inference complexity. But they a priori need to decide which binary code to associate to which category before learning using more or less complex heuristics. We propose a new end-to-end model which aims at simultaneously learning to associate binary codes with categories, but also learning to map inputs to binary codes. This approach called Deep Stochastic Neural Codes (DSNC) keeps the sublinear inference complexity but do not need any a priori tuning. Experimental results on different datasets show the effectiveness of the approach w.r.t baseline methods.

LSHTC: A Benchmark for Large-Scale Text Classification

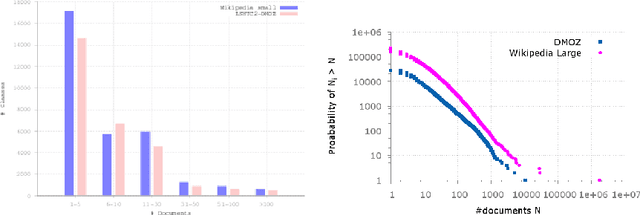
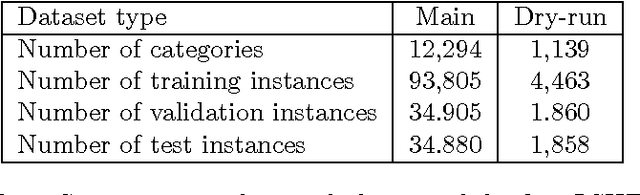
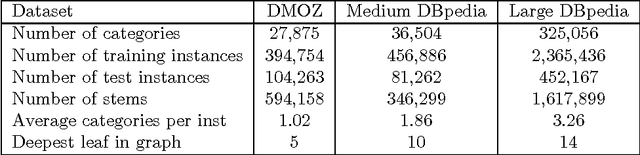
LSHTC is a series of challenges which aims to assess the performance of classification systems in large-scale classification in a a large number of classes (up to hundreds of thousands). This paper describes the dataset that have been released along the LSHTC series. The paper details the construction of the datsets and the design of the tracks as well as the evaluation measures that we implemented and a quick overview of the results. All of these datasets are available online and runs may still be submitted on the online server of the challenges.

An Empirical Comparison of V-fold Penalisation and Cross Validation for Model Selection in Distribution-Free Regression

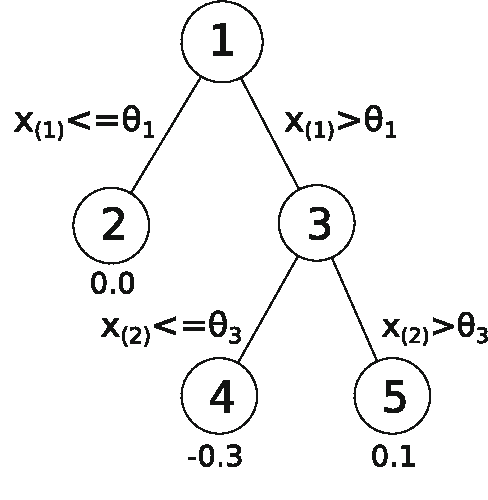
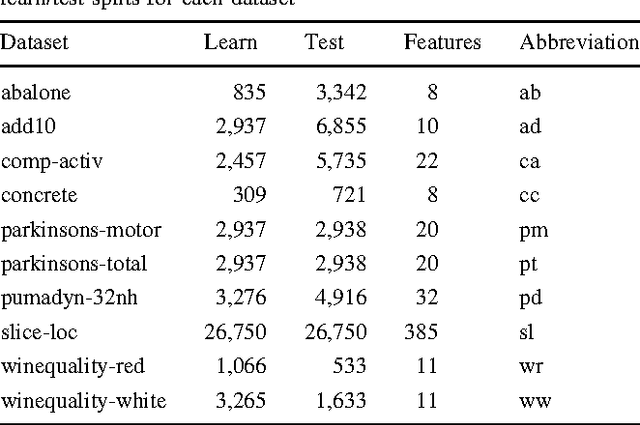
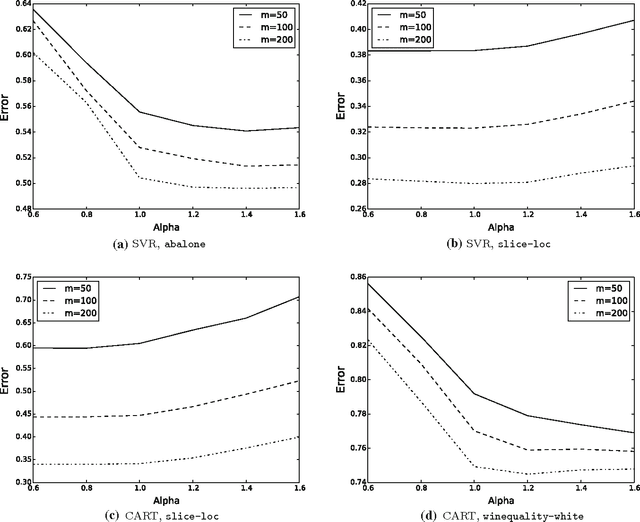
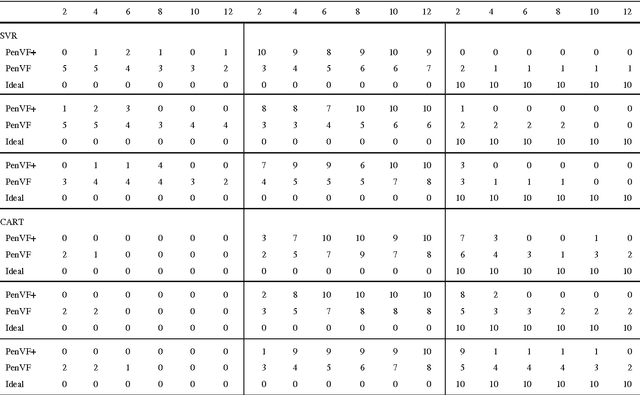
Model selection is a crucial issue in machine-learning and a wide variety of penalisation methods (with possibly data dependent complexity penalties) have recently been introduced for this purpose. However their empirical performance is generally not well documented in the literature. It is the goal of this paper to investigate to which extent such recent techniques can be successfully used for the tuning of both the regularisation and kernel parameters in support vector regression (SVR) and the complexity measure in regression trees (CART). This task is traditionally solved via V-fold cross-validation (VFCV), which gives efficient results for a reasonable computational cost. A disadvantage however of VFCV is that the procedure is known to provide an asymptotically suboptimal risk estimate as the number of examples tends to infinity. Recently, a penalisation procedure called V-fold penalisation has been proposed to improve on VFCV, supported by theoretical arguments. Here we report on an extensive set of experiments comparing V-fold penalisation and VFCV for SVR/CART calibration on several benchmark datasets. We highlight cases in which VFCV and V-fold penalisation provide poor estimates of the risk respectively and introduce a modified penalisation technique to reduce the estimation error.