Learning the Language of Protein Structure

Representation learning and \emph{de novo} generation of proteins are pivotal computational biology tasks. Whilst natural language processing (NLP) techniques have proven highly effective for protein sequence modelling, structure modelling presents a complex challenge, primarily due to its continuous and three-dimensional nature. Motivated by this discrepancy, we introduce an approach using a vector-quantized autoencoder that effectively tokenizes protein structures into discrete representations. This method transforms the continuous, complex space of protein structures into a manageable, discrete format with a codebook ranging from 4096 to 64000 tokens, achieving high-fidelity reconstructions with backbone root mean square deviations (RMSD) of approximately 1-5 \AA. To demonstrate the efficacy of our learned representations, we show that a simple GPT model trained on our codebooks can generate novel, diverse, and designable protein structures. Our approach not only provides representations of protein structure, but also mitigates the challenges of disparate modal representations and sets a foundation for seamless, multi-modal integration, enhancing the capabilities of computational methods in protein design.

Generalizing to New Physical Systems via Context-Informed Dynamics Model

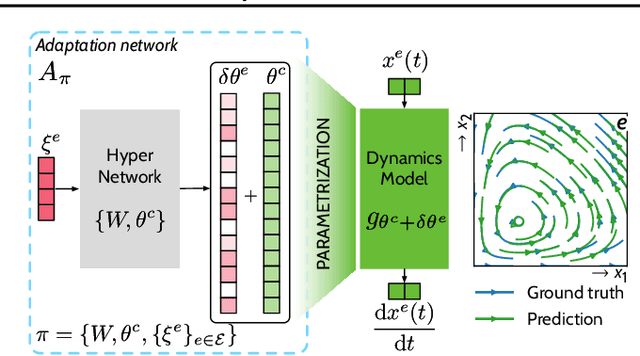
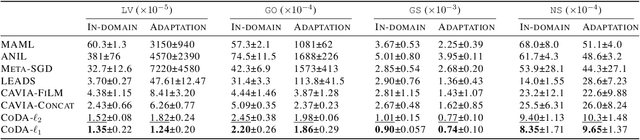
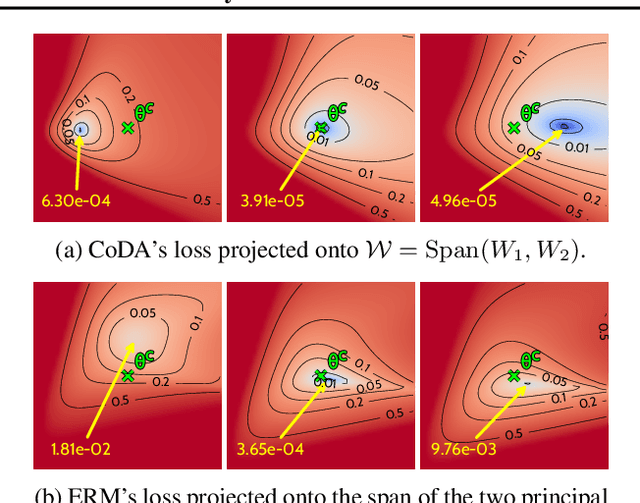
Data-driven approaches to modeling physical systems fail to generalize to unseen systems that share the same general dynamics with the learning domain, but correspond to different physical contexts. We propose a new framework for this key problem, context-informed dynamics adaptation (CoDA), which takes into account the distributional shift across systems for fast and efficient adaptation to new dynamics. CoDA leverages multiple environments, each associated to a different dynamic, and learns to condition the dynamics model on contextual parameters, specific to each environment. The conditioning is performed via a hypernetwork, learned jointly with a context vector from observed data. The proposed formulation constrains the search hypothesis space to foster fast adaptation and better generalization across environments. It extends the expressivity of existing methods. We theoretically motivate our approach and show state-ofthe-art generalization results on a set of nonlinear dynamics, representative of a variety of application domains. We also show, on these systems, that new system parameters can be inferred from context vectors with minimal supervision.

PDE-Driven Spatiotemporal Disentanglement

A recent line of work addresses the problem of predicting high-dimensional spatiotemporal phenomena by leveraging specific tools from the differential equations theory. Following this direction, we propose in this article a novel and general paradigm for this task based on a resolution method for partial differential equations: the separation of variables. This inspiration allows to introduce a dynamical interpretation of spatiotemporal disentanglement. It induces a simple and principled model based on learning disentangled spatial and temporal representations of a phenomenon to accurately predict future observations. We experimentally demonstrate the performance and broad applicability of our method against prior state-of-the-art models on physical and synthetic video datasets.