Learning the Language of Protein Structure

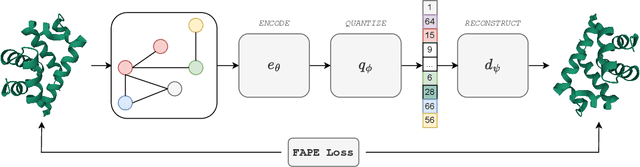
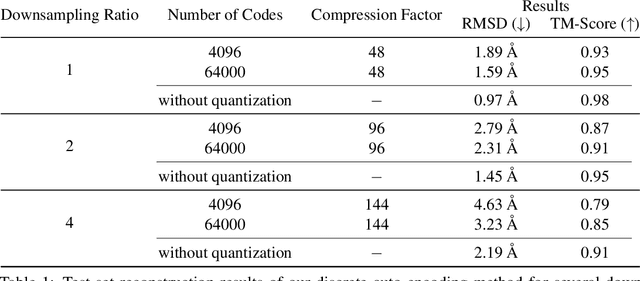
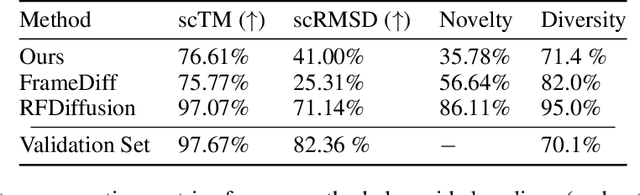
Representation learning and \emph{de novo} generation of proteins are pivotal computational biology tasks. Whilst natural language processing (NLP) techniques have proven highly effective for protein sequence modelling, structure modelling presents a complex challenge, primarily due to its continuous and three-dimensional nature. Motivated by this discrepancy, we introduce an approach using a vector-quantized autoencoder that effectively tokenizes protein structures into discrete representations. This method transforms the continuous, complex space of protein structures into a manageable, discrete format with a codebook ranging from 4096 to 64000 tokens, achieving high-fidelity reconstructions with backbone root mean square deviations (RMSD) of approximately 1-5 \AA. To demonstrate the efficacy of our learned representations, we show that a simple GPT model trained on our codebooks can generate novel, diverse, and designable protein structures. Our approach not only provides representations of protein structure, but also mitigates the challenges of disparate modal representations and sets a foundation for seamless, multi-modal integration, enhancing the capabilities of computational methods in protein design.

Learning Deep-Latent Hierarchies by Stacking Wasserstein Autoencoders

Probabilistic models with hierarchical-latent-variable structures provide state-of-the-art results amongst non-autoregressive, unsupervised density-based models. However, the most common approach to training such models based on Variational Autoencoders (VAEs) often fails to leverage deep-latent hierarchies; successful approaches require complex inference and optimisation schemes. Optimal Transport is an alternative, non-likelihood-based framework for training generative models with appealing theoretical properties, in principle allowing easier training convergence between distributions. In this work we propose a novel approach to training models with deep-latent hierarchies based on Optimal Transport, without the need for highly bespoke models and inference networks. We show that our method enables the generative model to fully leverage its deep-latent hierarchy, avoiding the well known "latent variable collapse" issue of VAEs; therefore, providing qualitatively better sample generations as well as more interpretable latent representation than the original Wasserstein Autoencoder with Maximum Mean Discrepancy divergence.

Learning disentangled representations with the Wasserstein Autoencoder

Disentangled representation learning has undoubtedly benefited from objective function surgery. However, a delicate balancing act of tuning is still required in order to trade off reconstruction fidelity versus disentanglement. Building on previous successes of penalizing the total correlation in the latent variables, we propose TCWAE (Total Correlation Wasserstein Autoencoder). Working in the WAE paradigm naturally enables the separation of the total-correlation term, thus providing disentanglement control over the learned representation, while offering more flexibility in the choice of reconstruction cost. We propose two variants using different KL estimators and perform extensive quantitative comparisons on data sets with known generative factors, showing competitive results relative to state-of-the-art techniques. We further study the trade off between disentanglement and reconstruction on more-difficult data sets with unknown generative factors, where the flexibility of the WAE paradigm in the reconstruction term improves reconstructions.

Gaussian mixture models with Wasserstein distance

Generative models with both discrete and continuous latent variables are highly motivated by the structure of many real-world data sets. They present, however, subtleties in training often manifesting in the discrete latent being under leveraged. In this paper, we show that such models are more amenable to training when using the Optimal Transport framework of Wasserstein Autoencoders. We find our discrete latent variable to be fully leveraged by the model when trained, without any modifications to the objective function or significant fine tuning. Our model generates comparable samples to other approaches while using relatively simple neural networks, since the discrete latent variable carries much of the descriptive burden. Furthermore, the discrete latent provides significant control over generation.