Continuous PDE Dynamics Forecasting with Implicit Neural Representations

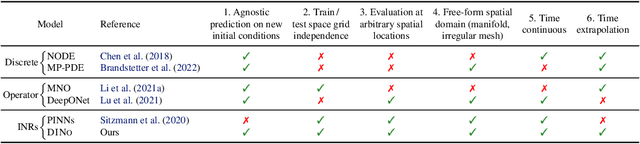
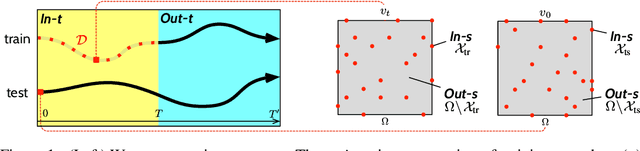
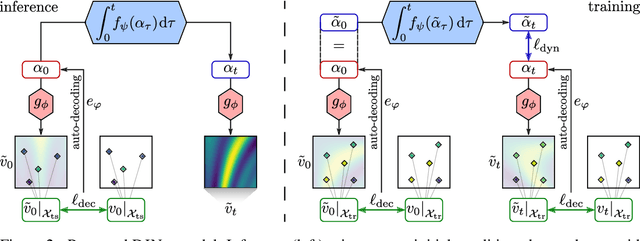
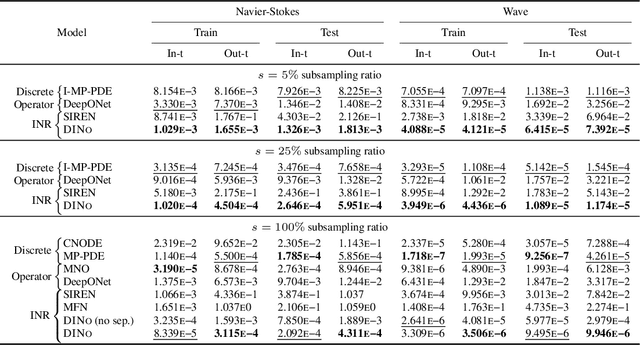
Effective data-driven PDE forecasting methods often rely on fixed spatial and / or temporal discretizations. This raises limitations in real-world applications like weather prediction where flexible extrapolation at arbitrary spatiotemporal locations is required. We address this problem by introducing a new data-driven approach, DINo, that models a PDE's flow with continuous-time dynamics of spatially continuous functions. This is achieved by embedding spatial observations independently of their discretization via Implicit Neural Representations in a small latent space temporally driven by a learned ODE. This separate and flexible treatment of time and space makes DINo the first data-driven model to combine the following advantages. It extrapolates at arbitrary spatial and temporal locations; it can learn from sparse irregular grids or manifolds; at test time, it generalizes to new grids or resolutions. DINo outperforms alternative neural PDE forecasters in a variety of challenging generalization scenarios on representative PDE systems.

Diverse Weight Averaging for Out-of-Distribution Generalization

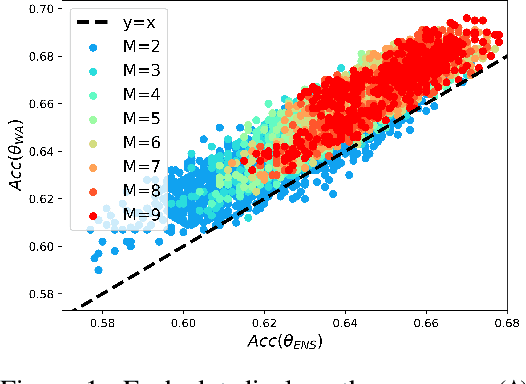
Standard neural networks struggle to generalize under distribution shifts. For out-of-distribution generalization in computer vision, the best current approach averages the weights along a training run. In this paper, we propose Diverse Weight Averaging (DiWA) that makes a simple change to this strategy: DiWA averages the weights obtained from several independent training runs rather than from a single run. Perhaps surprisingly, averaging these weights performs well under soft constraints despite the network's nonlinearities. The main motivation behind DiWA is to increase the functional diversity across averaged models. Indeed, models obtained from different runs are more diverse than those collected along a single run thanks to differences in hyperparameters and training procedures. We motivate the need for diversity by a new bias-variance-covariance-locality decomposition of the expected error, exploiting similarities between DiWA and standard functional ensembling. Moreover, this decomposition highlights that DiWA succeeds when the variance term dominates, which we show happens when the marginal distribution changes at test time. Experimentally, DiWA consistently improves the state of the art on the competitive DomainBed benchmark without inference overhead.

Generalizing to New Physical Systems via Context-Informed Dynamics Model

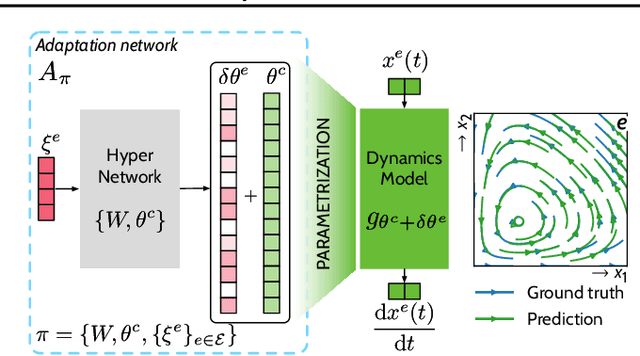
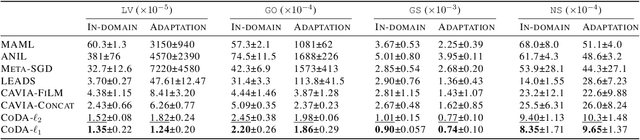
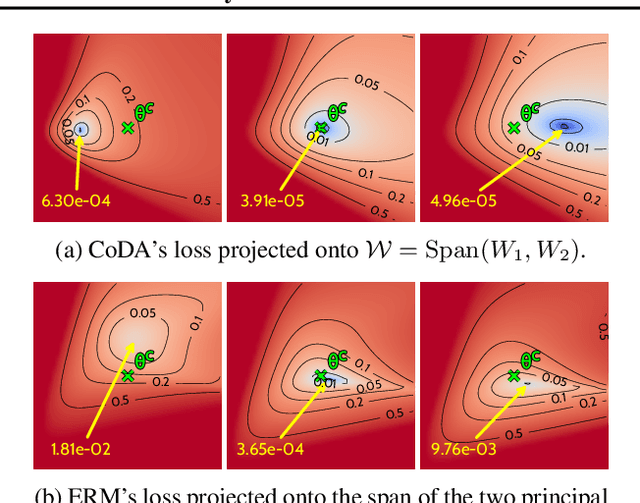
Data-driven approaches to modeling physical systems fail to generalize to unseen systems that share the same general dynamics with the learning domain, but correspond to different physical contexts. We propose a new framework for this key problem, context-informed dynamics adaptation (CoDA), which takes into account the distributional shift across systems for fast and efficient adaptation to new dynamics. CoDA leverages multiple environments, each associated to a different dynamic, and learns to condition the dynamics model on contextual parameters, specific to each environment. The conditioning is performed via a hypernetwork, learned jointly with a context vector from observed data. The proposed formulation constrains the search hypothesis space to foster fast adaptation and better generalization across environments. It extends the expressivity of existing methods. We theoretically motivate our approach and show state-ofthe-art generalization results on a set of nonlinear dynamics, representative of a variety of application domains. We also show, on these systems, that new system parameters can be inferred from context vectors with minimal supervision.

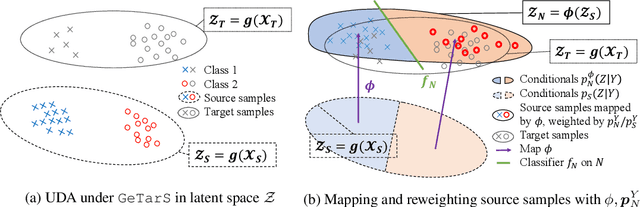
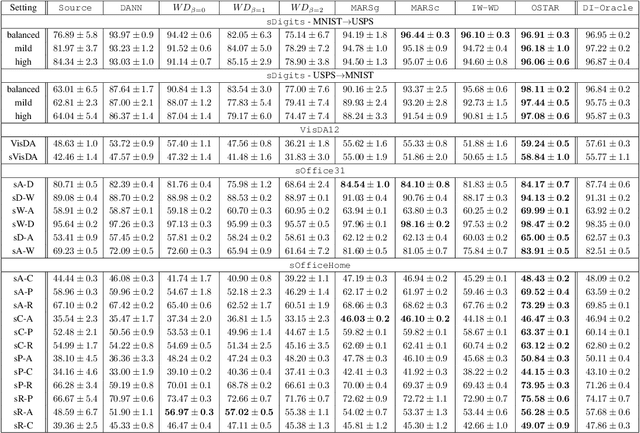
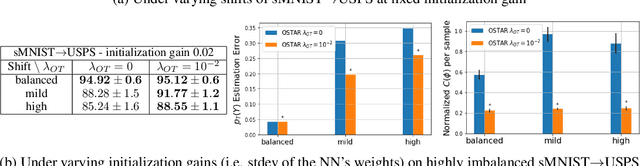
Mapping conditional distributions for domain adaptation under generalized target shift

We consider the problem of unsupervised domain adaptation (UDA) between a source and a target domain under conditional and label shift a.k.a Generalized Target Shift (GeTarS). Unlike simpler UDA settings, few works have addressed this challenging problem. Recent approaches learn domain-invariant representations, yet they have practical limitations and rely on strong assumptions that may not hold in practice. In this paper, we explore a novel and general approach to align pretrained representations, which circumvents existing drawbacks. Instead of constraining representation invariance, it learns an optimal transport map, implemented as a NN, which maps source representations onto target ones. Our approach is flexible and scalable, it preserves the problem's structure and it has strong theoretical guarantees under mild assumptions. In particular, our solution is unique, matches conditional distributions across domains, recovers target proportions and explicitly controls the target generalization risk. Through an exhaustive comparison on several datasets, we challenge the state-of-the-art in GeTarS.

Unsupervised domain adaptation with non-stochastic missing data

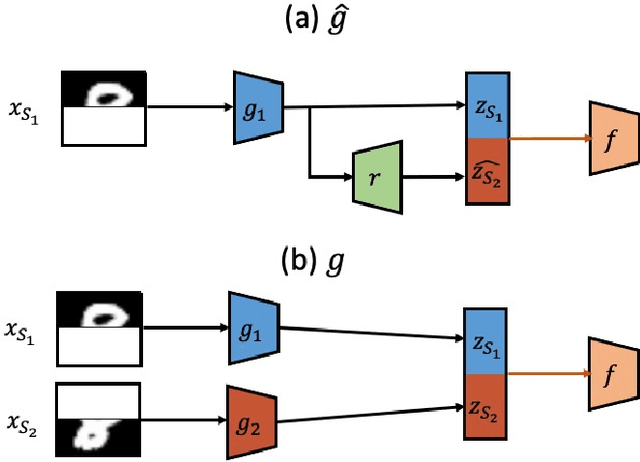
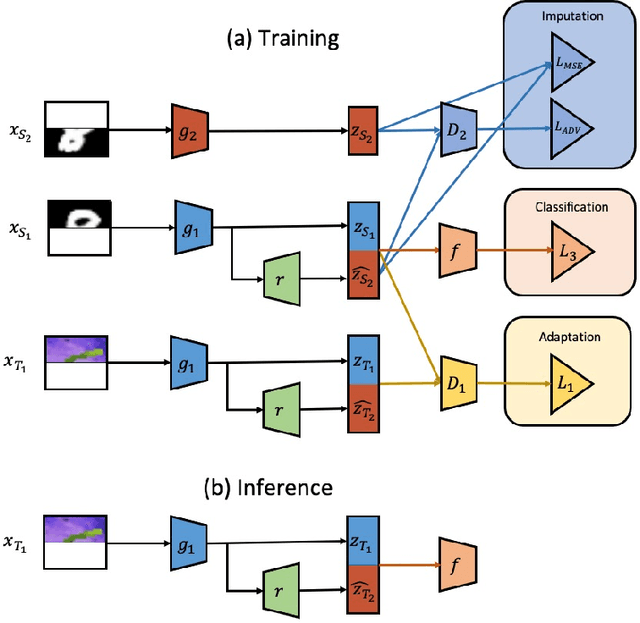
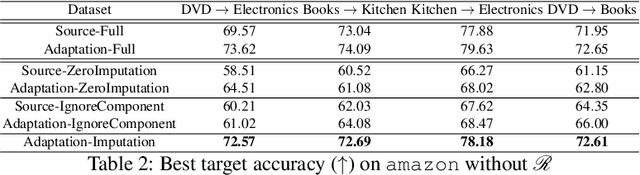
We consider unsupervised domain adaptation (UDA) for classification problems in the presence of missing data in the unlabelled target domain. More precisely, motivated by practical applications, we analyze situations where distribution shift exists between domains and where some components are systematically absent on the target domain without available supervision for imputing the missing target components. We propose a generative approach for imputation. Imputation is performed in a domain-invariant latent space and leverages indirect supervision from a complete source domain. We introduce a single model performing joint adaptation, imputation and classification which, under our assumptions, minimizes an upper bound of its target generalization error and performs well under various representative divergence families (H-divergence, Optimal Transport). Moreover, we compare the target error of our Adaptation-imputation framework and the "ideal" target error of a UDA classifier without missing target components. Our model is further improved with self-training, to bring the learned source and target class posterior distributions closer. We perform experiments on three families of datasets of different modalities: a classical digit classification benchmark, the Amazon product reviews dataset both commonly used in UDA and real-world digital advertising datasets. We show the benefits of jointly performing adaptation, classification and imputation on these datasets.

Regression with Conditional GAN

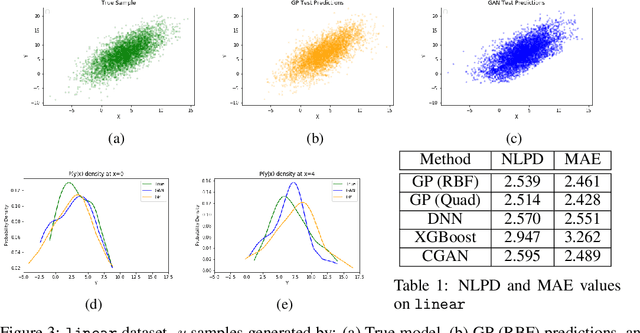
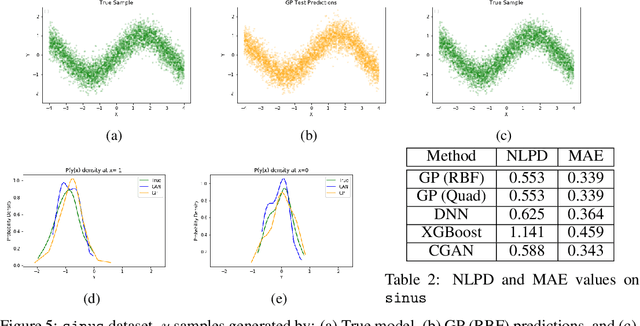
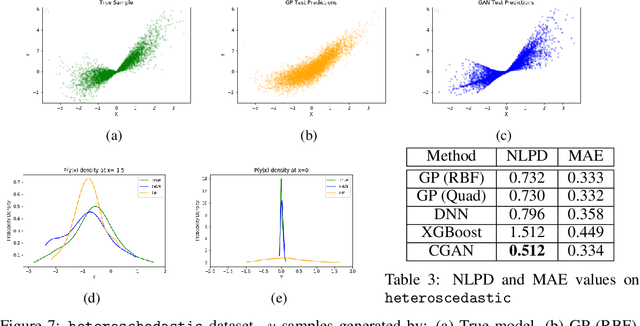
In recent years, impressive progress has been made in the design of implicit probabilistic models via Generative Adversarial Networks (GAN) and its extension, the Conditional GAN (CGAN). Excellent solutions have been demonstrated mostly in image processing applications which involve large, continuous output spaces. There is almost no application of these powerful tools to problems having small dimensional output spaces. Regression problems involving the inductive learning of a map, $y=f(x,z)$, $z$ denoting noise, $f:\mathbb{R}^n\times \mathbb{R}^k \rightarrow \mathbb{R}^m$, with $m$ small (e.g., $m=1$ or just a few) is one good case in point. The standard approach to solve regression problems is to probabilistically model the output $y$ as the sum of a mean function $m(x)$ and a noise term $z$; it is also usual to take the noise to be a Gaussian. These are done for convenience sake so that the likelihood of observed data is expressible in closed form. In the real world, on the other hand, stochasticity of the output is usually caused by missing or noisy input variables. Such a real world situation is best represented using an implicit model in which an extra noise vector, $z$ is included with $x$ as input. CGAN is naturally suited to design such implicit models. This paper makes the first step in this direction. Through several artificial and real world datasets, we demonstrate CGAN to be an effective approach for solving regression problems. We compare against Gaussian Processes and show that CGAN has excellent output likelihood properties and possesses the ability to model complex noise forms in a better way.