Amin Mantrach
Multilingual Self-Taught Faithfulness Evaluators
Jul 28, 2025Abstract:The growing use of large language models (LLMs) has increased the need for automatic evaluation systems, particularly to address the challenge of information hallucination. Although existing faithfulness evaluation approaches have shown promise, they are predominantly English-focused and often require expensive human-labeled training data for fine-tuning specialized models. As LLMs see increased adoption in multilingual contexts, there is a need for accurate faithfulness evaluators that can operate across languages without extensive labeled data. This paper presents Self-Taught Evaluators for Multilingual Faithfulness, a framework that learns exclusively from synthetic multilingual summarization data while leveraging cross-lingual transfer learning. Through experiments comparing language-specific and mixed-language fine-tuning approaches, we demonstrate a consistent relationship between an LLM's general language capabilities and its performance in language-specific evaluation tasks. Our framework shows improvements over existing baselines, including state-of-the-art English evaluators and machine translation-based approaches.
Monte Carlo Temperature: a robust sampling strategy for LLM's uncertainty quantification methods
Feb 25, 2025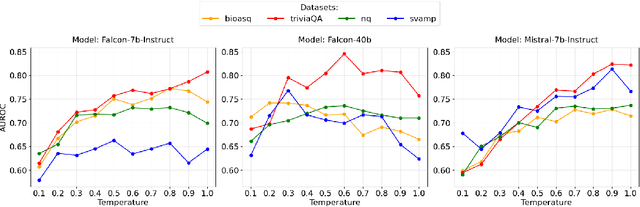
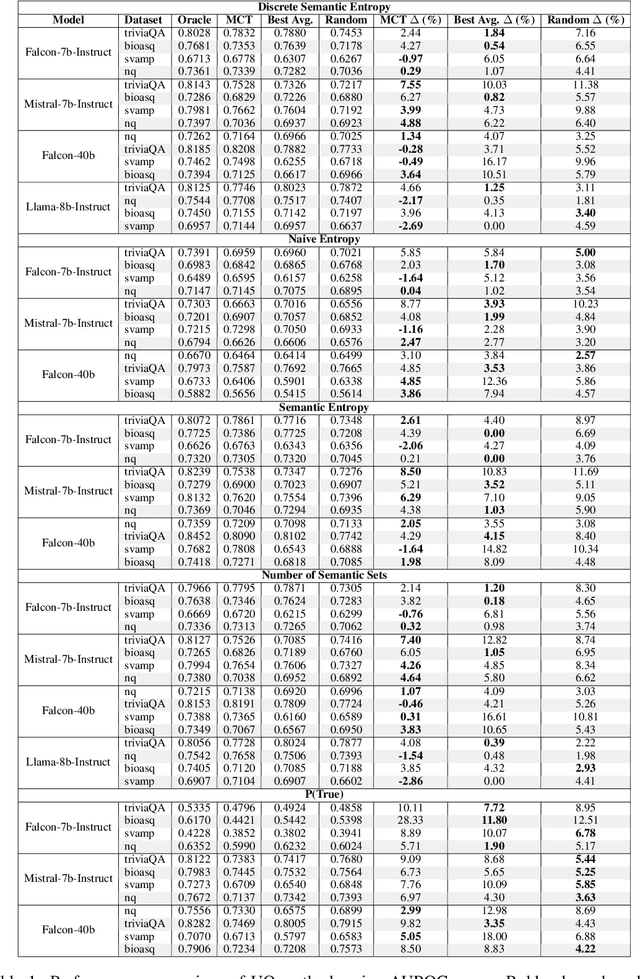
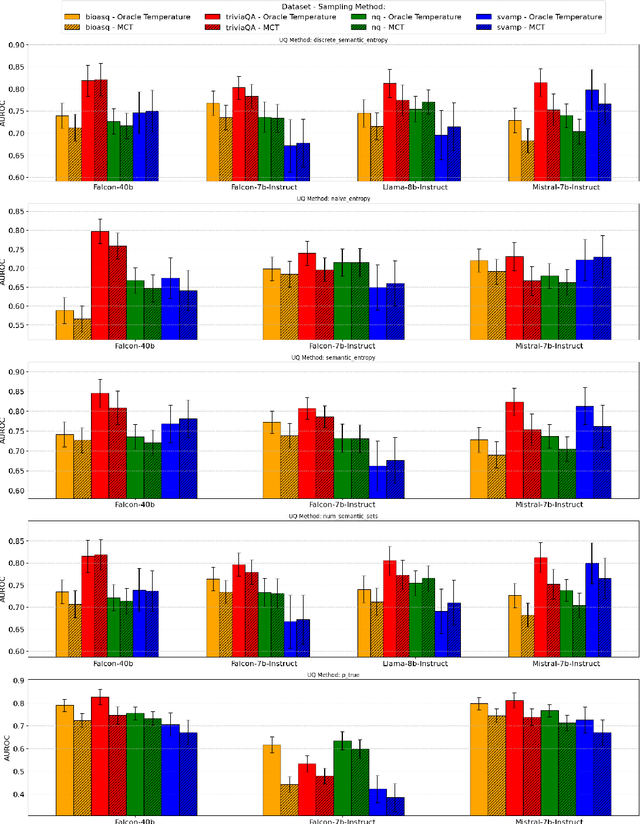
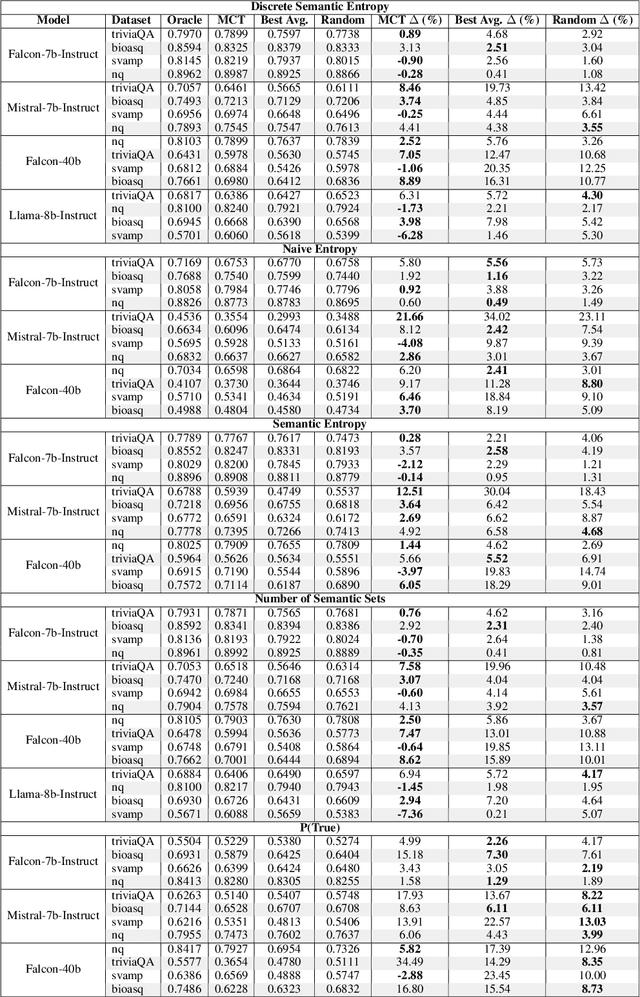
Abstract:Uncertainty quantification (UQ) in Large Language Models (LLMs) is essential for their safe and reliable deployment, particularly in critical applications where incorrect outputs can have serious consequences. Current UQ methods typically rely on querying the model multiple times using non-zero temperature sampling to generate diverse outputs for uncertainty estimation. However, the impact of selecting a given temperature parameter is understudied, and our analysis reveals that temperature plays a fundamental role in the quality of uncertainty estimates. The conventional approach of identifying optimal temperature values requires expensive hyperparameter optimization (HPO) that must be repeated for each new model-dataset combination. We propose Monte Carlo Temperature (MCT), a robust sampling strategy that eliminates the need for temperature calibration. Our analysis reveals that: 1) MCT provides more robust uncertainty estimates across a wide range of temperatures, 2) MCT improves the performance of UQ methods by replacing fixed-temperature strategies that do not rely on HPO, and 3) MCT achieves statistical parity with oracle temperatures, which represent the ideal outcome of a well-tuned but computationally expensive HPO process. These findings demonstrate that effective UQ can be achieved without the computational burden of temperature parameter calibration.
The Majority Vote Paradigm Shift: When Popular Meets Optimal
Feb 19, 2025



Abstract:Reliably labelling data typically requires annotations from multiple human workers. However, humans are far from being perfect. Hence, it is a common practice to aggregate labels gathered from multiple annotators to make a more confident estimate of the true label. Among many aggregation methods, the simple and well known Majority Vote (MV) selects the class label polling the highest number of votes. However, despite its importance, the optimality of MV's label aggregation has not been extensively studied. We address this gap in our work by characterising the conditions under which MV achieves the theoretically optimal lower bound on label estimation error. Our results capture the tolerable limits on annotation noise under which MV can optimally recover labels for a given class distribution. This certificate of optimality provides a more principled approach to model selection for label aggregation as an alternative to otherwise inefficient practices that sometimes include higher experts, gold labels, etc., that are all marred by the same human uncertainty despite huge time and monetary costs. Experiments on both synthetic and real world data corroborate our theoretical findings.
Unsupervised domain adaptation with non-stochastic missing data
Sep 16, 2021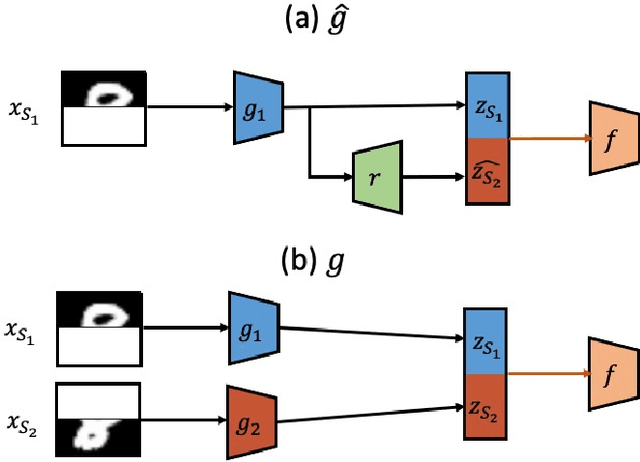

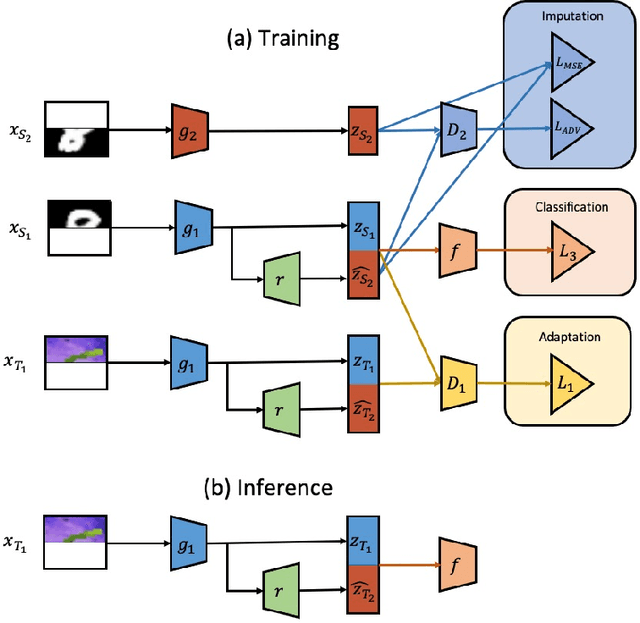
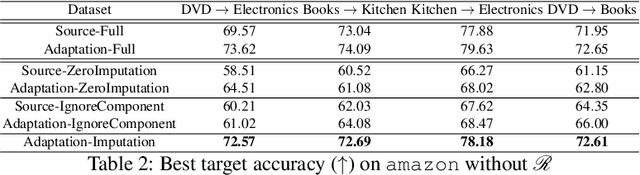
Abstract:We consider unsupervised domain adaptation (UDA) for classification problems in the presence of missing data in the unlabelled target domain. More precisely, motivated by practical applications, we analyze situations where distribution shift exists between domains and where some components are systematically absent on the target domain without available supervision for imputing the missing target components. We propose a generative approach for imputation. Imputation is performed in a domain-invariant latent space and leverages indirect supervision from a complete source domain. We introduce a single model performing joint adaptation, imputation and classification which, under our assumptions, minimizes an upper bound of its target generalization error and performs well under various representative divergence families (H-divergence, Optimal Transport). Moreover, we compare the target error of our Adaptation-imputation framework and the "ideal" target error of a UDA classifier without missing target components. Our model is further improved with self-training, to bring the learned source and target class posterior distributions closer. We perform experiments on three families of datasets of different modalities: a classical digit classification benchmark, the Amazon product reviews dataset both commonly used in UDA and real-world digital advertising datasets. We show the benefits of jointly performing adaptation, classification and imputation on these datasets.
Deep Character-Level Click-Through Rate Prediction for Sponsored Search
Jul 07, 2017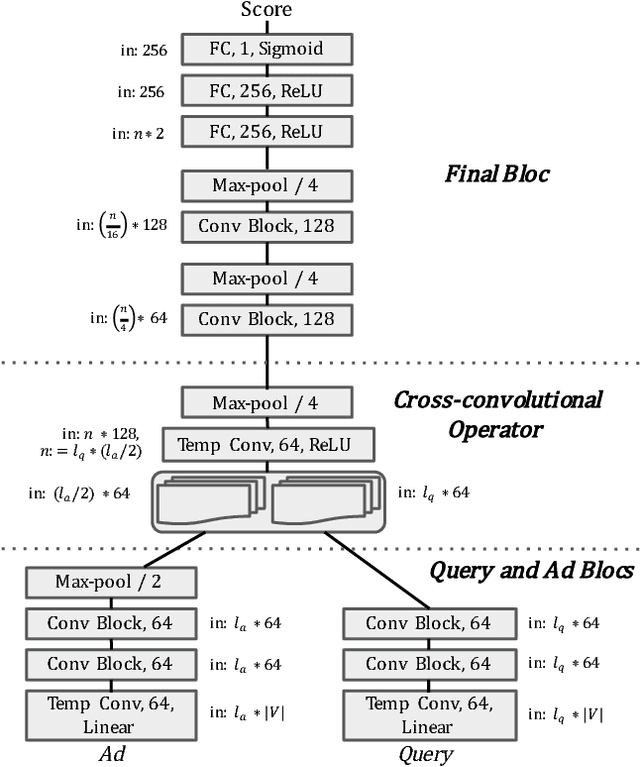
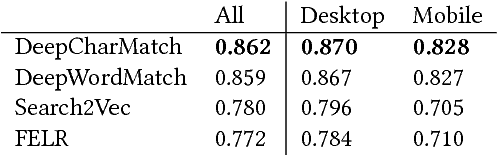


Abstract:Predicting the click-through rate of an advertisement is a critical component of online advertising platforms. In sponsored search, the click-through rate estimates the probability that a displayed advertisement is clicked by a user after she submits a query to the search engine. Commercial search engines typically rely on machine learning models trained with a large number of features to make such predictions. This is inevitably requires a lot of engineering efforts to define, compute, and select the appropriate features. In this paper, we propose two novel approaches (one working at character level and the other working at word level) that use deep convolutional neural networks to predict the click-through rate of a query-advertisement pair. Specially, the proposed architectures only consider the textual content appearing in a query-advertisement pair as input, and produce as output a click-through rate prediction. By comparing the character-level model with the word-level model, we show that language representation can be learnt from scratch at character level when trained on enough data. Through extensive experiments using billions of query-advertisement pairs of a popular commercial search engine, we demonstrate that both approaches significantly outperform a baseline model built on well-selected text features and a state-of-the-art word2vec-based approach. Finally, by combining the predictions of the deep models introduced in this study with the prediction of the model in production of the same commercial search engine, we significantly improve the accuracy and the calibration of the click-through rate prediction of the production system.
A bag-of-paths framework for network data analysis
Dec 14, 2016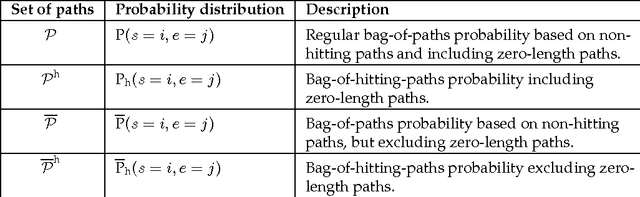

Abstract:This work develops a generic framework, called the bag-of-paths (BoP), for link and network data analysis. The central idea is to assign a probability distribution on the set of all paths in a network. More precisely, a Gibbs-Boltzmann distribution is defined over a bag of paths in a network, that is, on a representation that considers all paths independently. We show that, under this distribution, the probability of drawing a path connecting two nodes can easily be computed in closed form by simple matrix inversion. This probability captures a notion of relatedness between nodes of the graph: two nodes are considered as highly related when they are connected by many, preferably low-cost, paths. As an application, two families of distances between nodes are derived from the BoP probabilities. Interestingly, the second distance family interpolates between the shortest path distance and the resistance distance. In addition, it extends the Bellman-Ford formula for computing the shortest path distance in order to integrate sub-optimal paths by simply replacing the minimum operator by the soft minimum operator. Experimental results on semi-supervised classification show that both of the new distance families are competitive with other state-of-the-art approaches. In addition to the distance measures studied in this paper, the bag-of-paths framework enables straightforward computation of many other relevant network measures.
* Manuscript submitted for publication
Dynamic Matrix Factorization with Priors on Unknown Values
Jul 23, 2015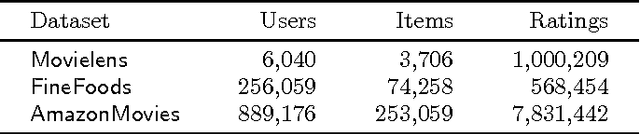
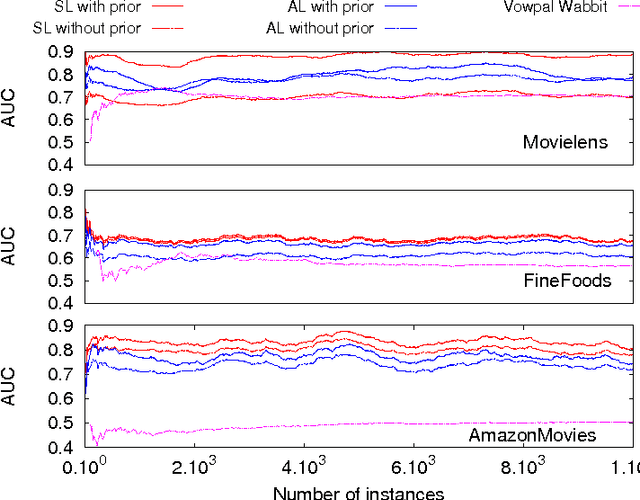
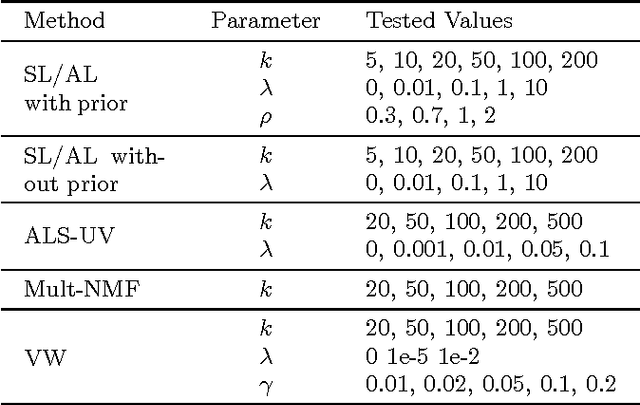
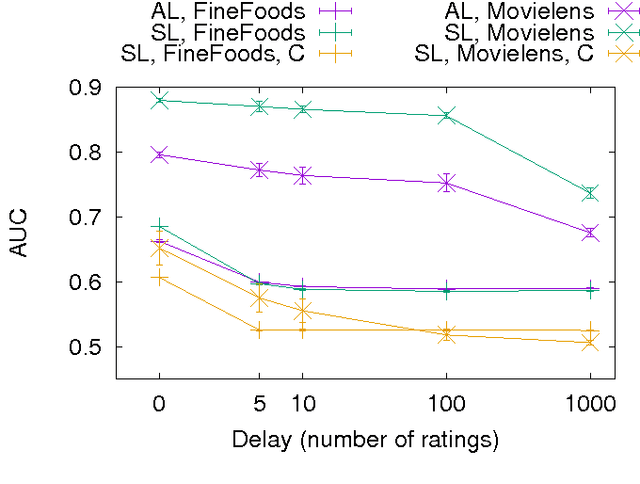
Abstract:Advanced and effective collaborative filtering methods based on explicit feedback assume that unknown ratings do not follow the same model as the observed ones (\emph{not missing at random}). In this work, we build on this assumption, and introduce a novel dynamic matrix factorization framework that allows to set an explicit prior on unknown values. When new ratings, users, or items enter the system, we can update the factorization in time independent of the size of data (number of users, items and ratings). Hence, we can quickly recommend items even to very recent users. We test our methods on three large datasets, including two very sparse ones, in static and dynamic conditions. In each case, we outrank state-of-the-art matrix factorization methods that do not use a prior on unknown ratings.
The Sum-over-Forests density index: identifying dense regions in a graph
Jan 04, 2013
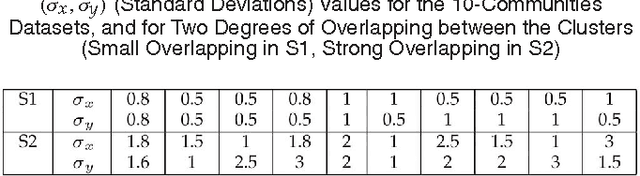
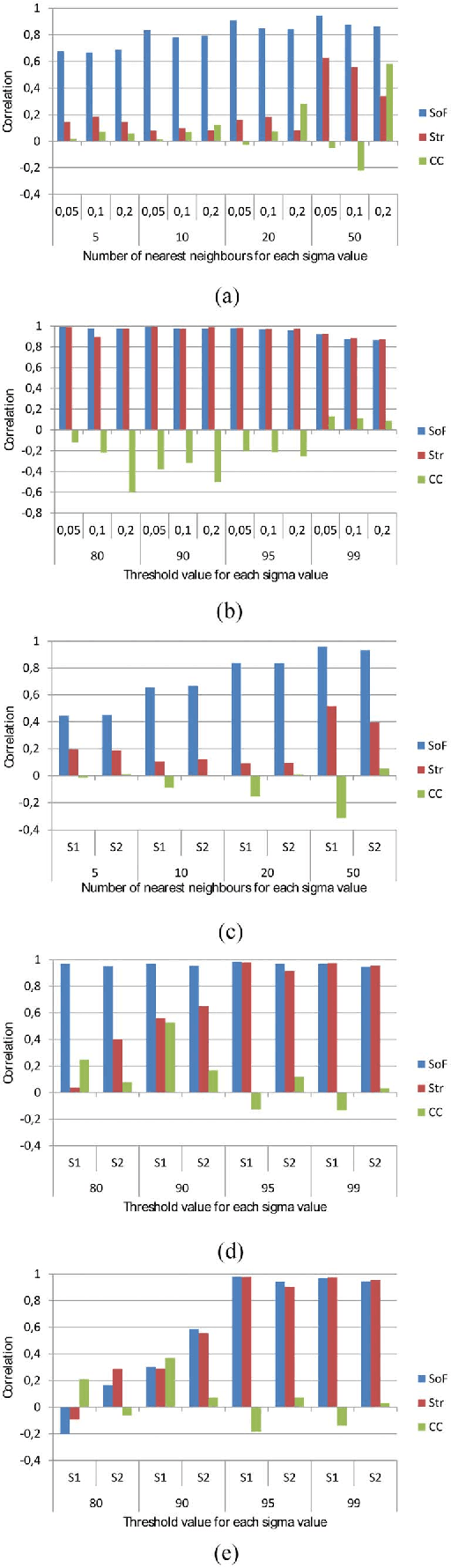
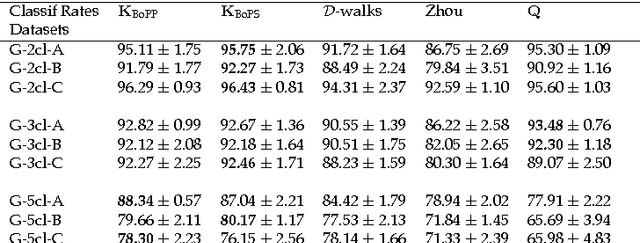
Abstract:This work introduces a novel nonparametric density index defined on graphs, the Sum-over-Forests (SoF) density index. It is based on a clear and intuitive idea: high-density regions in a graph are characterized by the fact that they contain a large amount of low-cost trees with high outdegrees while low-density regions contain few ones. Therefore, a Boltzmann probability distribution on the countable set of forests in the graph is defined so that large (high-cost) forests occur with a low probability while short (low-cost) forests occur with a high probability. Then, the SoF density index of a node is defined as the expected outdegree of this node in a non-trivial tree of the forest, thus providing a measure of density around that node. Following the matrix-forest theorem, and a statistical physics framework, it is shown that the SoF density index can be easily computed in closed form through a simple matrix inversion. Experiments on artificial and real data sets show that the proposed index performs well on finding dense regions, for graphs of various origins.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge