A bag-of-paths framework for network data analysis
Paper and Code
Dec 14, 2016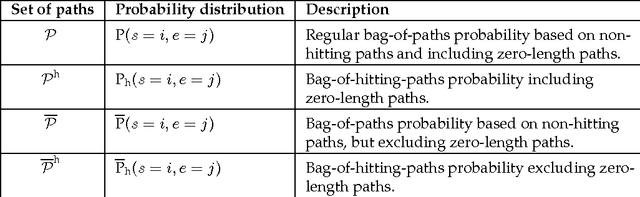

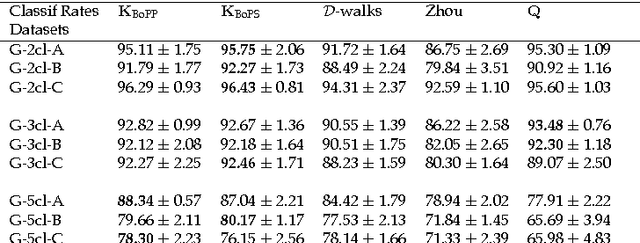
This work develops a generic framework, called the bag-of-paths (BoP), for link and network data analysis. The central idea is to assign a probability distribution on the set of all paths in a network. More precisely, a Gibbs-Boltzmann distribution is defined over a bag of paths in a network, that is, on a representation that considers all paths independently. We show that, under this distribution, the probability of drawing a path connecting two nodes can easily be computed in closed form by simple matrix inversion. This probability captures a notion of relatedness between nodes of the graph: two nodes are considered as highly related when they are connected by many, preferably low-cost, paths. As an application, two families of distances between nodes are derived from the BoP probabilities. Interestingly, the second distance family interpolates between the shortest path distance and the resistance distance. In addition, it extends the Bellman-Ford formula for computing the shortest path distance in order to integrate sub-optimal paths by simply replacing the minimum operator by the soft minimum operator. Experimental results on semi-supervised classification show that both of the new distance families are competitive with other state-of-the-art approaches. In addition to the distance measures studied in this paper, the bag-of-paths framework enables straightforward computation of many other relevant network measures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge