A Non-negative Matrix Factorization Based Method for Quantifying Rhythms of Activity and Sleep and Chronotypes Using Mobile Phone Data

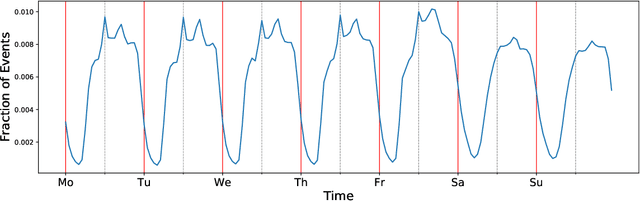
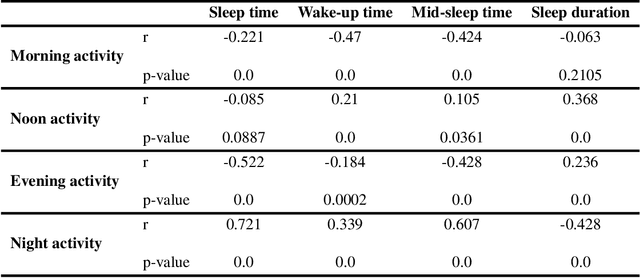
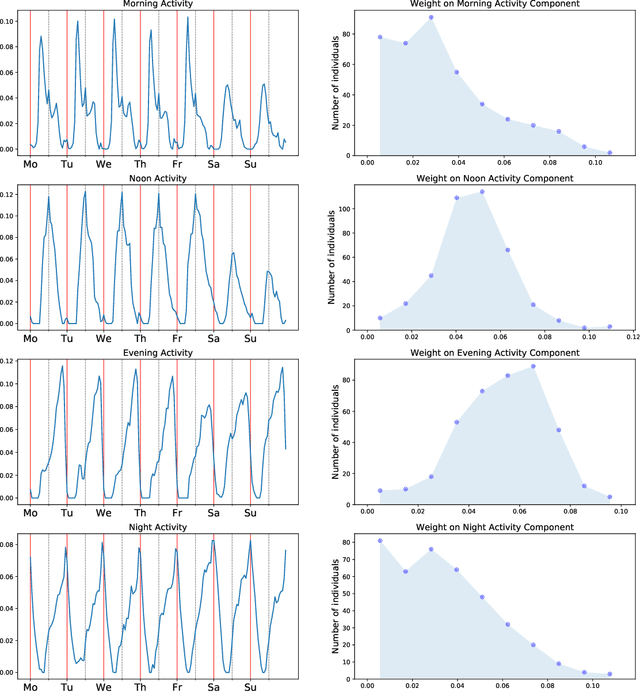
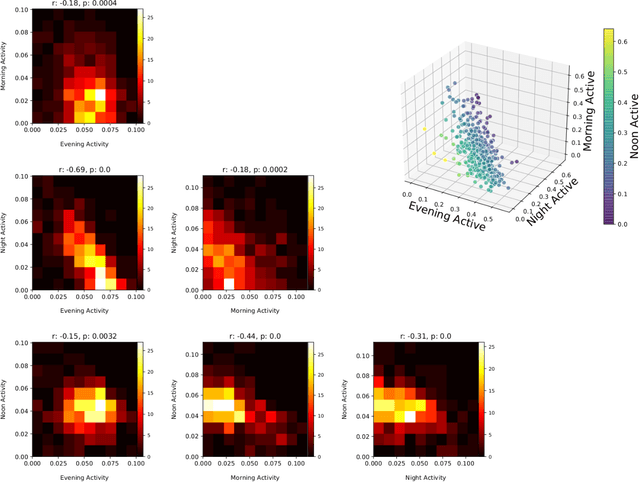
Human activities follow daily, weekly, and seasonal rhythms. The emergence of these rhythms is related to physiology and natural cycles as well as social constructs. The human body and biological functions undergo near 24-hour rhythms (circadian rhythms). The frequency of these rhythms is more or less similar across people, but its phase is different. In the chronobiology literature, based on the propensity to sleep at different hours of the day, people are categorized into morning-type, evening-type, and intermediate-type groups called \textit{chronotypes}. This typology is typically based on carefully designed questionnaires or manually crafted features drawing on data on timings of people's activity. Here we develop a fully data-driven (unsupervised) method to decompose individual temporal activity patterns into components. This has the advantage of not including any predetermined assumptions about sleep and activity hours, but the results are fully context-dependent and determined by the most prominent features of the activity data. Using a year-long dataset from mobile phone screen usage logs of 400 people, we find four emergent temporal components: morning activity, night activity, evening activity and activity at noon. Individual behavior can be reduced to weights on these four components. We do not observe any clear emergent categories of people based on the weights, but individuals are rather placed on a continuous spectrum according to the timings of their activities. High loads on morning and night components highly correlate with going to bed and waking up times. Our work points towards a data-driven way of categorizing people based on their full daily and weekly rhythms of activity and behavior, rather than focusing mainly on the timing of their sleeping periods.

A Constrained Randomized Shortest-Paths Framework for Optimal Exploration

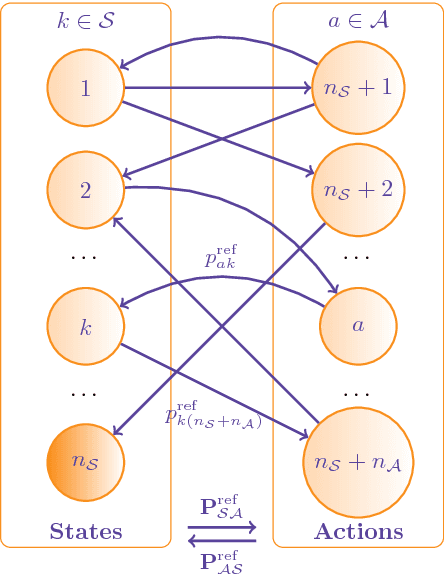
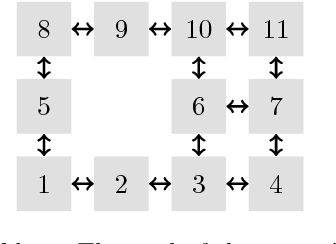
The present work extends the randomized shortest-paths framework (RSP), interpolating between shortest-path and random-walk routing in a network, in three directions. First, it shows how to deal with equality constraints on a subset of transition probabilities and develops a generic algorithm for solving this constrained RSP problem using Lagrangian duality. Second, it derives a surprisingly simple iterative procedure to compute the optimal, randomized, routing policy generalizing the previously developed "soft" Bellman-Ford algorithm. The resulting algorithm allows balancing exploitation and exploration in an optimal way by interpolating between a pure random behavior and the deterministic, optimal, policy (least-cost paths) while satisfying the constraints. Finally, the two algorithms are applied to Markov decision problems by considering the process as a constrained RSP on a bipartite state-action graph. In this context, the derived "soft" value iteration algorithm appears to be closely related to dynamic policy programming as well as Kullback-Leibler and path integral control, and similar to a recently introduced reinforcement learning exploration strategy. This shows that this strategy is optimal in the RSP sense - it minimizes expected path cost subject to relative entropy constraint. Simulation results on illustrative examples show that the model behaves as expected.

Randomized Optimal Transport on a Graph: Framework and New Distance Measures

The recently developed bag-of-paths framework consists in setting a Gibbs-Boltzmann distribution on all feasible paths of a graph. This probability distribution favors short paths over long ones, with a free parameter (the temperature $T > 0$) controlling the entropic level of the distribution. This formalism enables the computation of new distances or dissimilarities, interpolating between the shortest-path and the resistance distance, which have been shown to perform well in clustering and classification tasks. In this work, the bag-of-paths formalism is extended by adding two independent equality constraints fixing starting and ending nodes distributions of paths. When the temperature is low, this formalism is shown to be equivalent to a relaxation of the optimal transport problem on a network where paths carry a flow between two discrete distributions on nodes. The randomization is achieved by considering free energy minimization instead of traditional cost minimization. Algorithms computing the optimal free energy solution are developed for two types of paths: hitting (or absorbing) paths and non-hitting, regular paths, and require the inversion of an $n \times n$ matrix with $n$ being the number of nodes. Interestingly, for regular paths, the resulting optimal policy interpolates between the deterministic optimal transport policy ($T \rightarrow 0^{+}$) and the solution to the corresponding electrical circuit ($T \rightarrow \infty$). Two distance measures between nodes and a dissimilarity between groups of nodes, both integrating weights on nodes, are derived from this framework.

A bag-of-paths framework for network data analysis

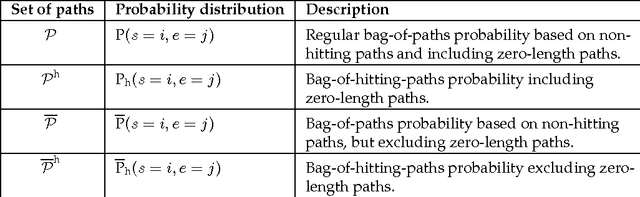
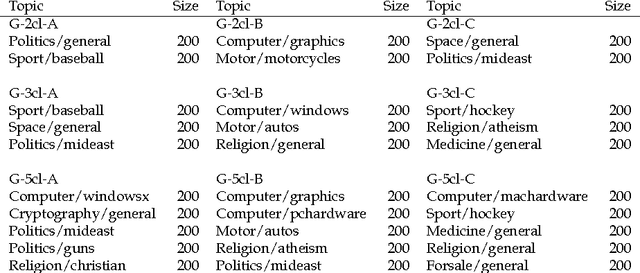
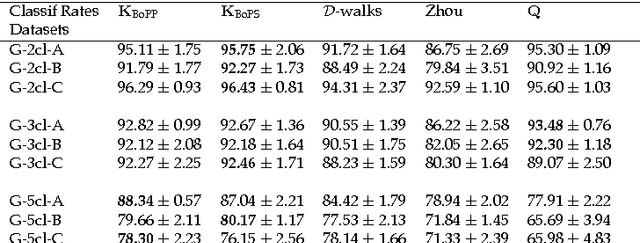
This work develops a generic framework, called the bag-of-paths (BoP), for link and network data analysis. The central idea is to assign a probability distribution on the set of all paths in a network. More precisely, a Gibbs-Boltzmann distribution is defined over a bag of paths in a network, that is, on a representation that considers all paths independently. We show that, under this distribution, the probability of drawing a path connecting two nodes can easily be computed in closed form by simple matrix inversion. This probability captures a notion of relatedness between nodes of the graph: two nodes are considered as highly related when they are connected by many, preferably low-cost, paths. As an application, two families of distances between nodes are derived from the BoP probabilities. Interestingly, the second distance family interpolates between the shortest path distance and the resistance distance. In addition, it extends the Bellman-Ford formula for computing the shortest path distance in order to integrate sub-optimal paths by simply replacing the minimum operator by the soft minimum operator. Experimental results on semi-supervised classification show that both of the new distance families are competitive with other state-of-the-art approaches. In addition to the distance measures studied in this paper, the bag-of-paths framework enables straightforward computation of many other relevant network measures.

Developments in the theory of randomized shortest paths with a comparison of graph node distances

There have lately been several suggestions for parametrized distances on a graph that generalize the shortest path distance and the commute time or resistance distance. The need for developing such distances has risen from the observation that the above-mentioned common distances in many situations fail to take into account the global structure of the graph. In this article, we develop the theory of one family of graph node distances, known as the randomized shortest path dissimilarity, which has its foundation in statistical physics. We show that the randomized shortest path dissimilarity can be easily computed in closed form for all pairs of nodes of a graph. Moreover, we come up with a new definition of a distance measure that we call the free energy distance. The free energy distance can be seen as an upgrade of the randomized shortest path dissimilarity as it defines a metric, in addition to which it satisfies the graph-geodetic property. The derivation and computation of the free energy distance are also straightforward. We then make a comparison between a set of generalized distances that interpolate between the shortest path distance and the commute time, or resistance distance. This comparison focuses on the applicability of the distances in graph node clustering and classification. The comparison, in general, shows that the parametrized distances perform well in the tasks. In particular, we see that the results obtained with the free energy distance are among the best in all the experiments.

Semi-Supervised Classification Through the Bag-of-Paths Group Betweenness

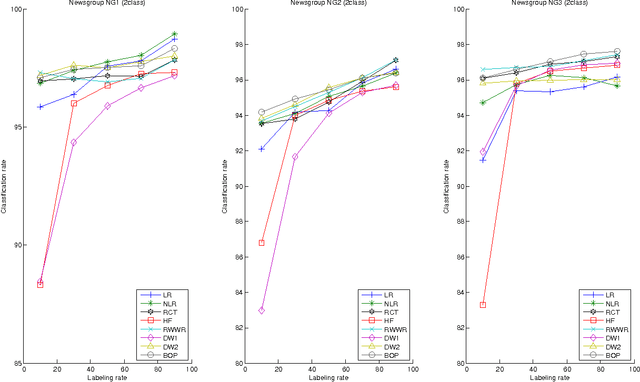
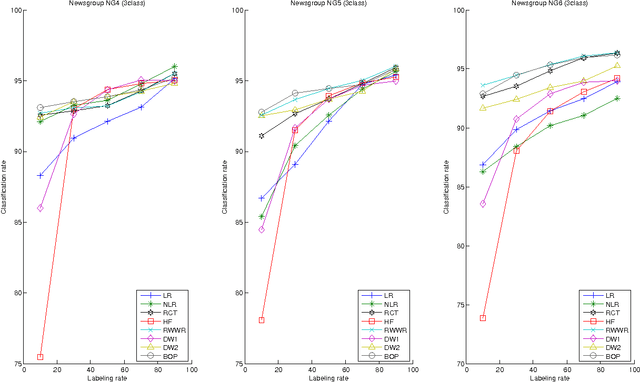
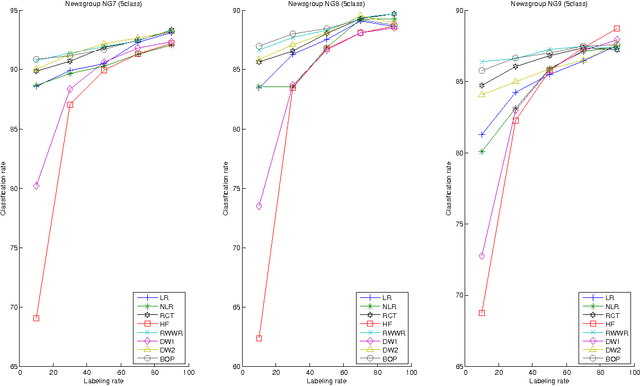
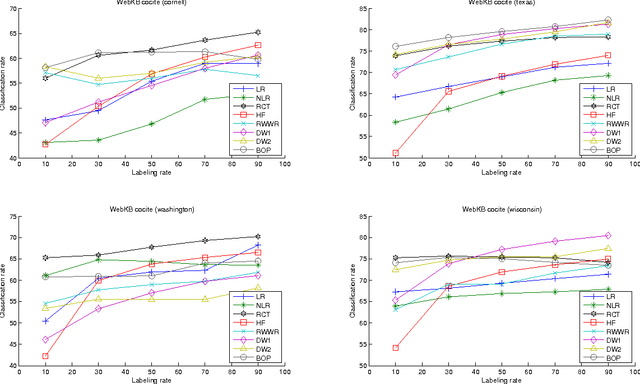
This paper introduces a novel, well-founded, betweenness measure, called the Bag-of-Paths (BoP) betweenness, as well as its extension, the BoP group betweenness, to tackle semisupervised classification problems on weighted directed graphs. The objective of semi-supervised classification is to assign a label to unlabeled nodes using the whole topology of the graph and the labeled nodes at our disposal. The BoP betweenness relies on a bag-of-paths framework assigning a Boltzmann distribution on the set of all possible paths through the network such that long (high-cost) paths have a low probability of being picked from the bag, while short (low-cost) paths have a high probability of being picked. Within that context, the BoP betweenness of node j is defined as the sum of the a posteriori probabilities that node j lies in-between two arbitrary nodes i, k, when picking a path starting in i and ending in k. Intuitively, a node typically receives a high betweenness if it has a large probability of appearing on paths connecting two arbitrary nodes of the network. This quantity can be computed in closed form by inverting a n x n matrix where n is the number of nodes. For the group betweenness, the paths are constrained to start and end in nodes within the same class, therefore defining a group betweenness for each class. Unlabeled nodes are then classified according to the class showing the highest group betweenness. Experiments on various real-world data sets show that BoP group betweenness outperforms all the tested state of-the-art methods. The benefit of the BoP betweenness is particularly noticeable when only a few labeled nodes are available.