Semi-Supervised Classification Through the Bag-of-Paths Group Betweenness
Paper and Code
Oct 16, 2012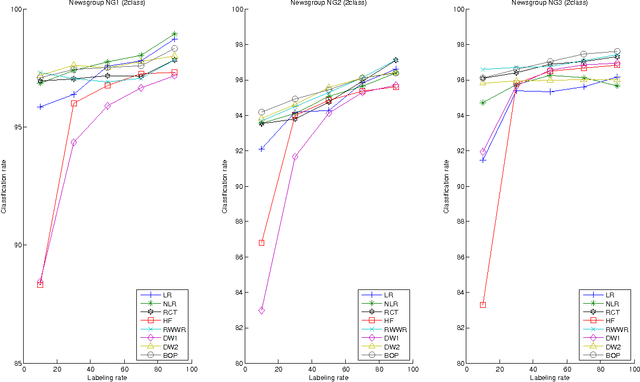
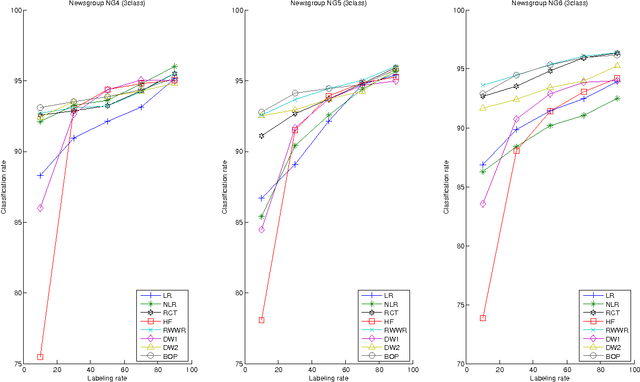
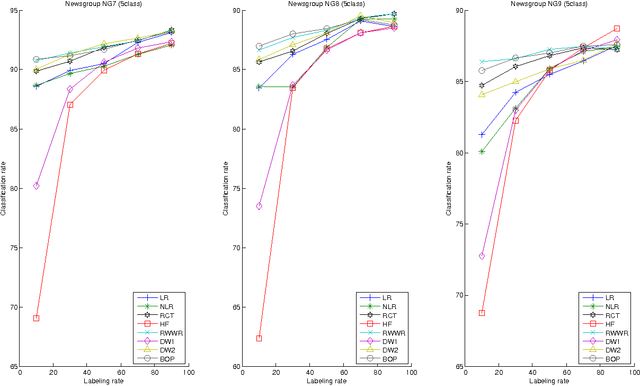
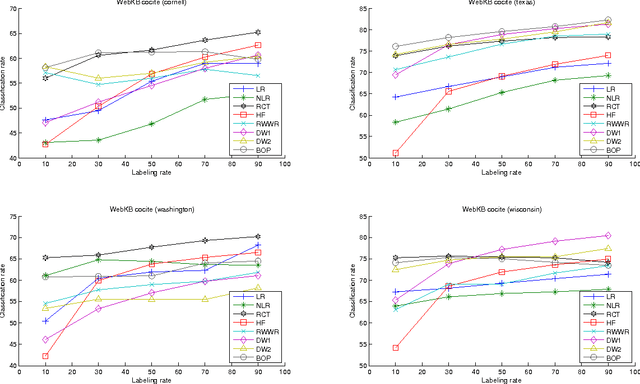
This paper introduces a novel, well-founded, betweenness measure, called the Bag-of-Paths (BoP) betweenness, as well as its extension, the BoP group betweenness, to tackle semisupervised classification problems on weighted directed graphs. The objective of semi-supervised classification is to assign a label to unlabeled nodes using the whole topology of the graph and the labeled nodes at our disposal. The BoP betweenness relies on a bag-of-paths framework assigning a Boltzmann distribution on the set of all possible paths through the network such that long (high-cost) paths have a low probability of being picked from the bag, while short (low-cost) paths have a high probability of being picked. Within that context, the BoP betweenness of node j is defined as the sum of the a posteriori probabilities that node j lies in-between two arbitrary nodes i, k, when picking a path starting in i and ending in k. Intuitively, a node typically receives a high betweenness if it has a large probability of appearing on paths connecting two arbitrary nodes of the network. This quantity can be computed in closed form by inverting a n x n matrix where n is the number of nodes. For the group betweenness, the paths are constrained to start and end in nodes within the same class, therefore defining a group betweenness for each class. Unlabeled nodes are then classified according to the class showing the highest group betweenness. Experiments on various real-world data sets show that BoP group betweenness outperforms all the tested state of-the-art methods. The benefit of the BoP betweenness is particularly noticeable when only a few labeled nodes are available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge