Kevin Françoisse
A bag-of-paths framework for network data analysis
Dec 14, 2016

Abstract:This work develops a generic framework, called the bag-of-paths (BoP), for link and network data analysis. The central idea is to assign a probability distribution on the set of all paths in a network. More precisely, a Gibbs-Boltzmann distribution is defined over a bag of paths in a network, that is, on a representation that considers all paths independently. We show that, under this distribution, the probability of drawing a path connecting two nodes can easily be computed in closed form by simple matrix inversion. This probability captures a notion of relatedness between nodes of the graph: two nodes are considered as highly related when they are connected by many, preferably low-cost, paths. As an application, two families of distances between nodes are derived from the BoP probabilities. Interestingly, the second distance family interpolates between the shortest path distance and the resistance distance. In addition, it extends the Bellman-Ford formula for computing the shortest path distance in order to integrate sub-optimal paths by simply replacing the minimum operator by the soft minimum operator. Experimental results on semi-supervised classification show that both of the new distance families are competitive with other state-of-the-art approaches. In addition to the distance measures studied in this paper, the bag-of-paths framework enables straightforward computation of many other relevant network measures.
* Manuscript submitted for publication
Semi-Supervised Classification Through the Bag-of-Paths Group Betweenness
Oct 16, 2012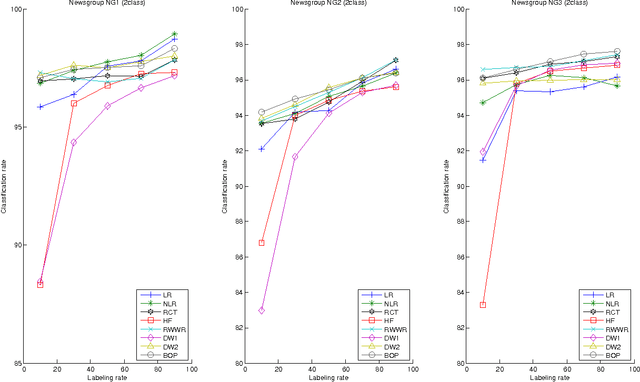
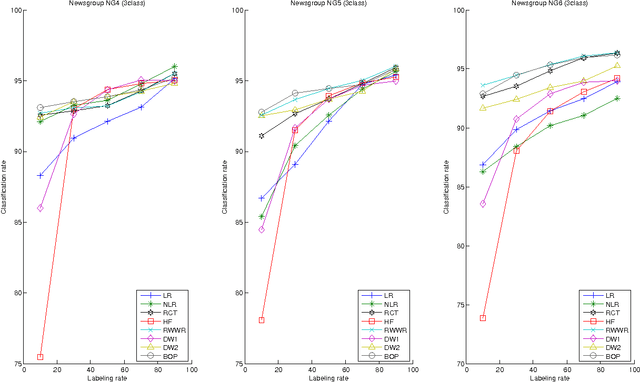
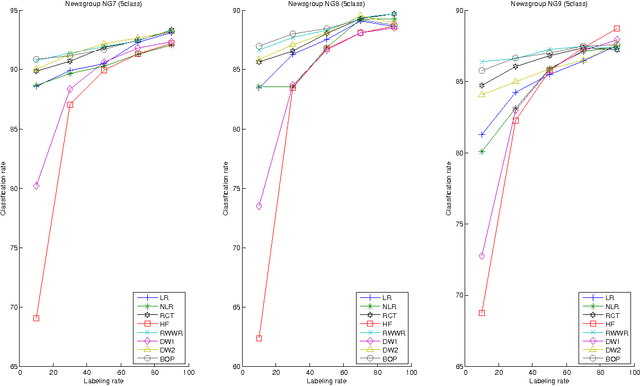
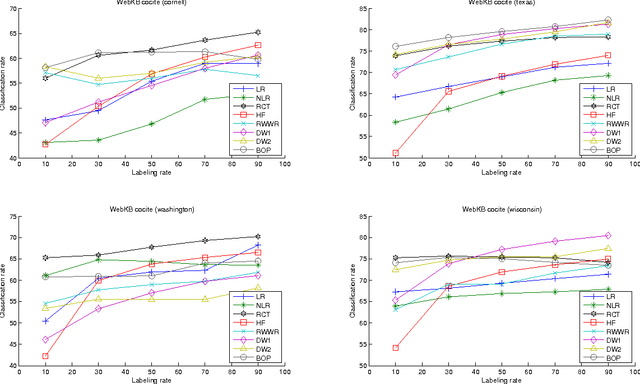
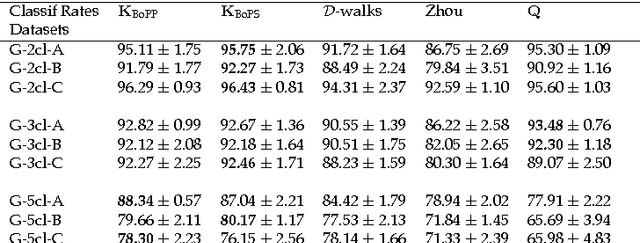
Abstract:This paper introduces a novel, well-founded, betweenness measure, called the Bag-of-Paths (BoP) betweenness, as well as its extension, the BoP group betweenness, to tackle semisupervised classification problems on weighted directed graphs. The objective of semi-supervised classification is to assign a label to unlabeled nodes using the whole topology of the graph and the labeled nodes at our disposal. The BoP betweenness relies on a bag-of-paths framework assigning a Boltzmann distribution on the set of all possible paths through the network such that long (high-cost) paths have a low probability of being picked from the bag, while short (low-cost) paths have a high probability of being picked. Within that context, the BoP betweenness of node j is defined as the sum of the a posteriori probabilities that node j lies in-between two arbitrary nodes i, k, when picking a path starting in i and ending in k. Intuitively, a node typically receives a high betweenness if it has a large probability of appearing on paths connecting two arbitrary nodes of the network. This quantity can be computed in closed form by inverting a n x n matrix where n is the number of nodes. For the group betweenness, the paths are constrained to start and end in nodes within the same class, therefore defining a group betweenness for each class. Unlabeled nodes are then classified according to the class showing the highest group betweenness. Experiments on various real-world data sets show that BoP group betweenness outperforms all the tested state of-the-art methods. The benefit of the BoP betweenness is particularly noticeable when only a few labeled nodes are available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge