A Constrained Randomized Shortest-Paths Framework for Optimal Exploration
Paper and Code
Jul 12, 2018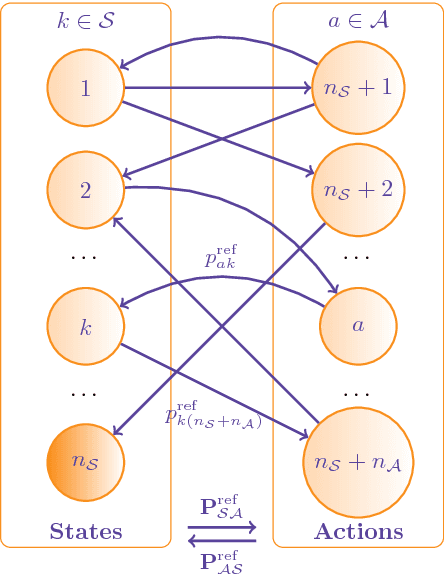
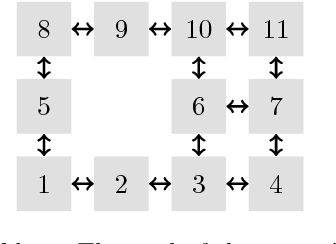
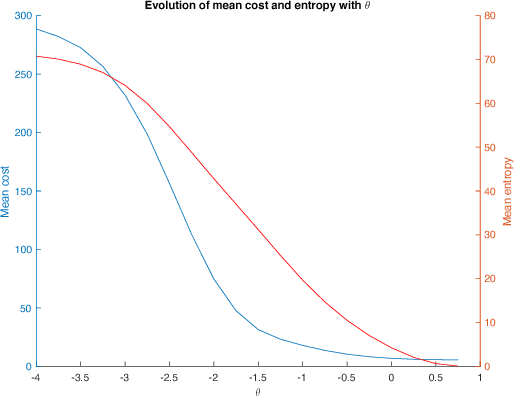

The present work extends the randomized shortest-paths framework (RSP), interpolating between shortest-path and random-walk routing in a network, in three directions. First, it shows how to deal with equality constraints on a subset of transition probabilities and develops a generic algorithm for solving this constrained RSP problem using Lagrangian duality. Second, it derives a surprisingly simple iterative procedure to compute the optimal, randomized, routing policy generalizing the previously developed "soft" Bellman-Ford algorithm. The resulting algorithm allows balancing exploitation and exploration in an optimal way by interpolating between a pure random behavior and the deterministic, optimal, policy (least-cost paths) while satisfying the constraints. Finally, the two algorithms are applied to Markov decision problems by considering the process as a constrained RSP on a bipartite state-action graph. In this context, the derived "soft" value iteration algorithm appears to be closely related to dynamic policy programming as well as Kullback-Leibler and path integral control, and similar to a recently introduced reinforcement learning exploration strategy. This shows that this strategy is optimal in the RSP sense - it minimizes expected path cost subject to relative entropy constraint. Simulation results on illustrative examples show that the model behaves as expected.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge